Логические схемы строятся на основе логических элементов, набор которых определяется заданным логическим базисом. Наиболее распространенной в алгебре логики является функционально полная система логических функций, которая в качестве базовых логических функций использует функцию одной переменной « НЕ» (функция отрицания), и две функции двух переменных «И» (конъюнкция или логическое умножения) и «ИЛИ» (дизъюнкция или логическое сложение). Эта система получила название система Булевых функций или Булевый базис. В алгебре логики имеется целый раздел «алгебра Буля» посвященный этому базису. Для базиса Буля в качестве логических элементов используются элементы, реализующие базовые логические функции И, ИЛИ, НЕ, которые приведены на рисунке 1.1,а–в, соответственно.

г) д) е)
Рисунок 1.1 – Условные графические обозначения основных логических элементов
При синтезе схемы по логическому выражению, логические операции представляются в виде соответствующих логических элементов, связи между которыми определяются последовательностью выполнения логических операций в заданном выражении. В качестве примера рассмотрим синтез логической схемы, определяемой выражением (1.1), в базисе И, ИЛИ, НЕ. Схема имеет три входных сигнала – x1, x2, x3, представленные в прямой и инверсной форме, и один выходной – fСДНФ. Реализацию заданного выражения в виде логической схемы можно начать или с первой, или с последней операции. Первой операцией является инверсия входных переменных (используются три элемента НЕ). Следующая операция – формирование конъюнкций, для чего используются четыре трехвходовые элемента И. Последней операцией в заданном выражении является операция логического сложения четырех операндов (используется один четырехвходовой элемент ИЛИ). Схема синтезируемого выражения приведена на рисунке 1.2.
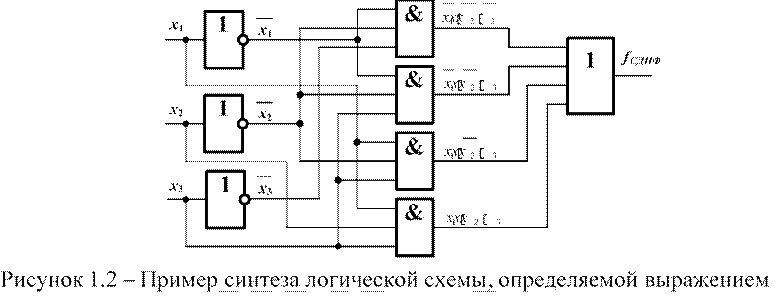
fСДНФ x1x2 x3 x1x2 x3 x1x2 x3 x1x2 x3
Очевидно, среди схем, реализующих данную функцию, есть наиболее простая. Поиск логической формулы, соответствующей этой схеме, представляет большой практический интерес.
1.3 Минимизация логических функций
Сложность логической схемы можно оценить по количеству требуемого оборудования, подсчитав суммарное количество всех элементарных компонентов (например, транзисторов), входящих в эту схему. Для КМОП-технологии: элемент НЕ состоит из двух транзисторов, элемент 2И-НЕ (2ИЛИ-НЕ) из четырех транзисторов, элемент 3И-НЕ (3ИЛИ-НЕ) из шести транзисторов и т.д. Часто сложность схемы оценивают по числу логических элементов, используемых для реализации схемы. Например, схема на рис.1.2 состоит из восьми элементов (три инвертора, четыре элемента И и один элемент ИЛИ).
Быстродействие комбинационной схемы определяется максимальным временем задержки распространения сигнала от любого из входов до любого выхода. Следовательно, оценить быстродействие логической схемы можно рассчитав максимальное значение суммы времен задержек всех элементов, расположенных между каждым входом и выходом схемы. Например, будем считать, что время задержки всех логических элементов на рис.1.2 одинаково и равно t. Тогда максимальное время задержки распространения сигнала равно 3t.
Следующий параметр, подлежащий минимизации – энергопотребление, которое зависит как от параметров входных сигналов (в частности, от частоты входных сигналов), так и от схемной реализации логической функции. Причем, минимизация одного параметра, как правило, конфликтует с другими параметрами. Например, минимизация энергопотребления приводит к снижению быстродействия. Таким образом, при проектировании логических схем стоит задача многокритериальной оптимизации при заданных ограничениях. Получить оптимальное решение по всем параметрам практически невозможно. Поэтому решается задача оптимизации по одному параметру (например, аппаратные затраты). Такая частная оптимизация называется минимизацией.
Далее рассмотрим только одну оптимизационную задачу – минимизацию
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.