Теперь осталось нарисовать логическую схему в базисе И, ИЛИ, НЕ в соответствии с полученным выражением (рисунок 1.7).
 Рисунок 1.7 – Схема
формирования старшего разряда произведения
Рисунок 1.7 – Схема
формирования старшего разряда произведения
По аналогии синтезируются схемы для остальных разрядов.
1. Изучить теоретические сведения.
2. Разработать программу для составления таблицы истинности синтезируемой комбинационной схемы согласно его определению, назначению и описанию принципов работы.
3. На основании таблицы истинности составить математические формулы для логических функций.
4. Минимизировать полученные логические выражения.
5. Нарисовать логическую схему в базисе И, ИЛИ, НЕ.
6. Разработать программу, моделирующую работу схемы, для верификации.
7. Подготовить отчет, который должен содержать цель, задание, краткие теоретические сведения, алгоритмы работы программ, результаты работы программ, логическую схему (выполненную вручную или при помощи редактора Visio), выводы по работе.
В отчете должны быть отображены следующие пункты:
1. Задание.
2. Краткие теоретические сведения.
3. Схемы алгоритмов и листинги основных частей программы.
4. Результаты работы программ.
5. Логические функции до и после минимизации, а также подробно расписан процесс минимизации одной из функций (определяет преподаватель).
6. Схема умножителя.
7. Выводы.
1. Какие бывают формы представления логических функций?
2. В чем состоит отличие ДНФ и КНФ?
3. Как записать функцию в КНФ по таблице истинности? 3. Как записать функцию в ДНФ по таблице истинности?
5. Что такое тупиковая ДНФ?
6. Что такое код Грея? Привести примеры.
7. В чем состоит отличие кода Грея от двоичного кода?
8. Сколько клеток должна иметь карта Карно для функции n переменных?
9. Сколько клеток можно обвести на карте Карно?
10. Можно ли обвести клетки, содержащие «1» и расположенные в самой верхней и самой нижней строке одного столбца?
Лабораторная работа № 2 «Базовые комбинационные схемы ЭВМ» (2 часа)
Цель работы: Изучить базовые комбинационные схемы ЭВМ
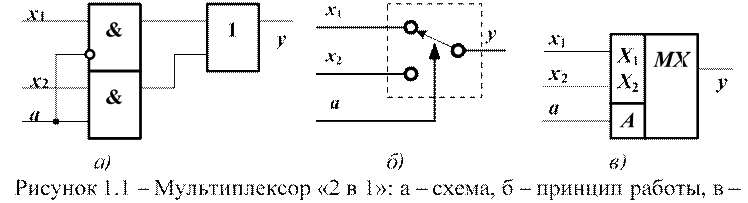
Мультиплексор – функциональный узел, осуществляющий передачу сигнала с любого информационного входа на один выход [1]. Входы мультиплексора подразделяются на информационные и адресные. Адресные входы определяют номер информационного входа, с которого информация попадает на выход. Схема простейшего мультиплексора, содержащего два информационных входа, представлена на рисунке 1.1,а. На рисунке 1.1,б представлено упрощенное представление принципа работы этого мультиплексора. Значение адресного входа a определяет позицию переключателя: при a=0 переключатель находится в верхнем положении. Поэтому на выход попадает информация с входа x1. При a=1 переключатель находится в нижнем положении, поэтому на выход попадает информация со входа x2. На рисунке 1.1,в представлено условное графическое обозначение (УГО) этого мультиплексора, в таблице 1.1 представлена таблица истинности.
функциональное обозначение
Таблица 1.1 – Таблица истинности мультиплексора «2 в 1»
|
а |
x1 |
x2 |
y |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
В общем случае мультиплексор при помощи n адресных входов позволяет выбирать один из 2n информационных сигналов. Промышленностью выпускаются мультиплексоры, имеющие 2, 4, 8 и 16 информационных входов. Для реализации мультиплексоров большей разрядности применяют различные схемы. Наибольшее распространение получила пирамидальная схема наращивания разрядности. Рассмотрим пример построения мультиплексора «8 в 1» из мультиплексоров «2 в 1» (рисунок 1.2). В общем случае первый ярус пирамиды состоит из k мультиплексоров. Значение k определяется из соотношения k=n/m, где n – требуемое число входов, m – число входов имеющихся мультиплексоров. Таким образом, первый ярус содержит k мультиплексоров «m в 1». Следующий ярус содержит k/m мультиплексоров «m в 1» и т.д. Последний ярус содержит один мультиплексор «m в 1». В нашем случае: n=8, m=2, поэтому будет три яруса, причем в первом ярусе k=4 мультиплексора «2 в 1», во втором ярусе – два, в третьем ярусе – один. На рисунке 1.2,а приведена пирамидальная схема мультиплексора, а на рисунке 1.2,б – его условное графическое обозначение.
На основе мультиплексоров строят универсальные логические модули (УЛМ). Универсальность этих модулей заключается в том, что они могут быть настроены на реализацию произвольной логической функции. Самым простым способом настройки УЛМ является фиксация информационных входов. При этом на адресные входы мультиплексора подаются аргументы функции, а на информационные входы – таблица настройки. Рассмотрим пример настройки мультиплексора на реализацию функции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.