Построение минимального остового дерева. Изучение основных алгоритмов построение минимальных остовых деревьев

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО

Факультет автоматизированных и информационных систем

Кафедра «Информационные технологии»

ОТЧЕТ   ПО   ЛАБОРАТОРНОЙ   РАБОТЕ   № 4

по дисциплине «Конструирование программ я языки программирования»

на тему:     «Построение минимального остового дерева»

Выполнил:     студент гр. ИТ-32

Приняла:                                                                                              преподаватель

Гомель 2013

Лабораторная   работа   № 4

Построение минимального остового дерева

Цель: Изучение основных алгоритмов построение минимальных остовых деревьев

Задание:

1.  Для неориентированного графа сохранить его в виде списка смежности.

2.  Реализовать алгоритмы поиска минимальных остовых деревьев (Прима–Краскала, Прима, Дейкстры-Прима, Краскала)

Количество вершин 8, количество связей 10.

2 -> 8 (5)

1 -> 4 (1)

2 -> 6 (3)

3 - > 8 (7)

7 -> 5 (7)

8 -> 4 (3)

6 -> 5 (2)

4 -> 3 (13)

3 -> 2 (1)

Список смежности

1->4

2->8, 6, 3

3->8, 2, 4

4->1, 8, 3

5->7, 6

6->2, 5

7->5

8->2, 4, 3

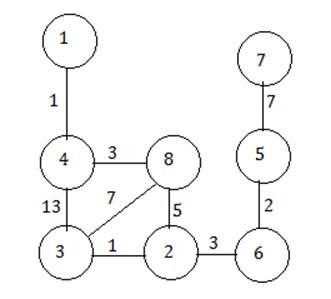
Алгоритм Прима.

Стартовая вершина 1.

Из 1 существует путь только в 4. Выбираем ребро 1-4.

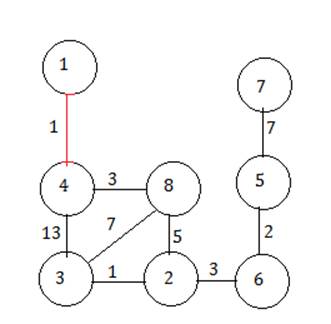
Выбираем из ребер 4-8 и 4-3. Выбираем то, вес которого меньше – 4-8.

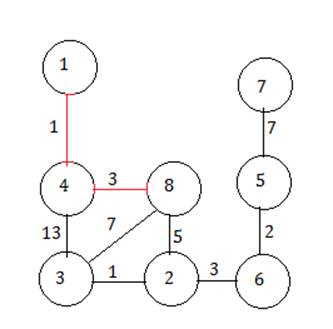
Выбираем из ребер 4-3, 8-3 и 8-2. Выбираем 8-2.

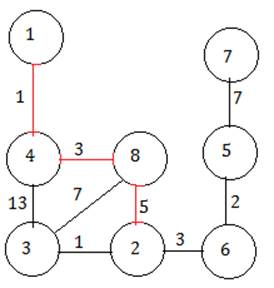
Выбираем из ребер 4-3, 8-3, 2-3, 2-6. Выбираем 2-3.

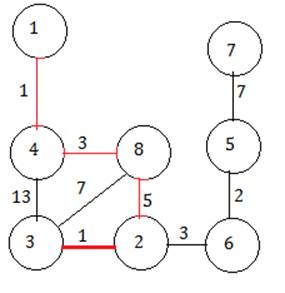
Ребра 4-3 и 8-3 брать нельзя, т.к. образуется цикл. Поэтому выбираем ребро 2-6. Затем 6-5, затем 5-7.

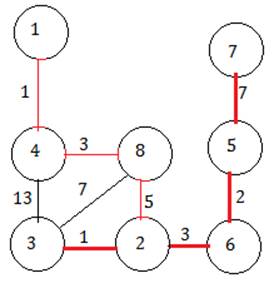
Класс Graph

using System;

using System.Collections.Generic;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

namespace lab4

{

    class Graph

    {

        List<Edge> edges;

        int vCount;

        public Graph(List<Edge> edges, int vCount)

        {

            this.edges = edges;

            this.vCount = vCount;

        }

        /// <summary>

        /// Алгоритм Прима

        /// </summary>

        /// <returns></returns>

        public string Prim(string start)

        {

            string res = "";

            int length = 0;

            List<string> visited = new List<string>();//Список вершин, в которые ходили

            visited.Add(start);//Начинаем с первой в списке

            while (visited.Count < vCount)//Пока не посетили все вершины...

            {

                int min = Int32.MaxValue;//Принимаем заведомо большое число

                int iMin = -1;

                //Ищем следующее ребро

                for (int i = 0; i < edges.Count; ++i)

                {

                    //Если из этой вершины мы можем пойти, и это не создаст цикла в дереве...

                    if (visited.Contains(edges[i].StartV) && !visited.Contains(edges[i].EndV))

                    {

                        if (edges[i].Weight < min)//выбираем то, вес которого минимален

                        {

                            min = edges[i].Weight;

                            iMin = i;

                        }

                    }

                }

                    visited.Add(edges[iMin].EndV);

                    length += edges[iMin].Weight;

                    res += edges[iMin].StartV + "->" + edges[iMin].EndV + "\n";

            }

            res += "Вес минимального остового дерева равен " + length;

            return res;

        }

        /// <summary>

        /// Алгоритм Прима-Краскала

        /// </summary>

        /// <returns></returns>

        public string PrimKraskal()

        {

            string res = "";

            int length = 0;

            List<string> visited = new List<string>();

            List<Edge> sortedEdg = new List<Edge>();

            //Записываем ребра по возрастанию веса

            while (sortedEdg.Count < edges.Count)

            {

                int min = Int32.MaxValue;

                int iMin = -1;

                for (int i = 0; i < edges.Count; ++i)

                {

                    if (!sortedEdg.Contains(edges[i]))

                    {

                        if (edges[i].Weight < min)

                        {

                            min = edges[i].Weight;

                            iMin = i;

                        }

                    }

                }

                sortedEdg.Add(edges[iMin]);

            }

            visited.Add(sortedEdg[0].StartV);

            visited.Add(sortedEdg[0].EndV);

            res += sortedEdg[0].StartV + "->" + sortedEdg[0].EndV + "\n";

            length += sortedEdg[0].Weight;

            while (visited.Count < vCount)

            {

                for (int i = 0; i < sortedEdg.Count; ++i)

                {