Поиск оптимальных путей в графе. Алгоритм Дейкстры. Инициализация. Шаг алгоритма

Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.

Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.

Пример:

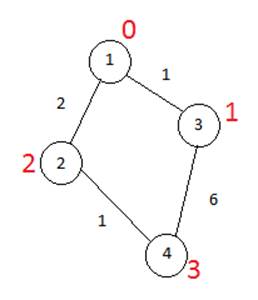
Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.

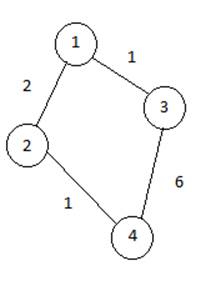
Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.

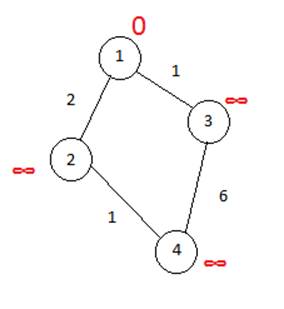
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2 и 3.

Первый по очереди сосед вершины 1 — вершина 3, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1, значению её метки, и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 1 = 1. Это меньше текущей метки вершины 3, бесконечности, поэтому новая метка 3-й вершины равна 1.

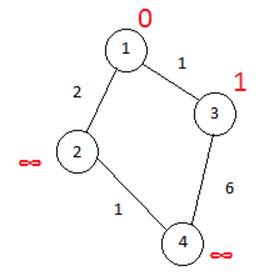
Аналогичную операцию проделываем с вершиной 2. Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.

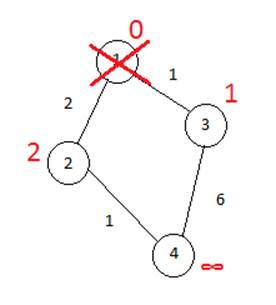
Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 2.

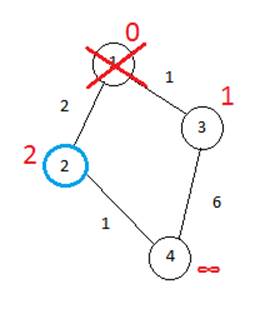
Проделываем аналогичные действия: ищем ближайшие вершины, соединенные со 2-й, и устанавливаем путь до них. Конечный вид графа будет следующим:

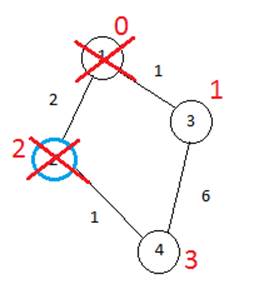
То же самое с 3-й вершиной. Однако теперь мы сравниваем текущий вес вершины 4 (3) с новым – 7 и так как он выше, то вес вершины 4 остается прежним.

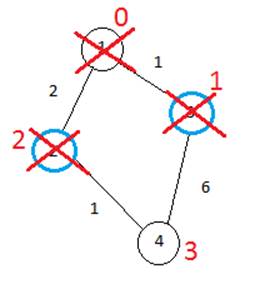
А так как от у вершины 4 нет больше смежных с ней вершин то обход закончен. Кротчайшие расстояния до каждой из вершин найдены.

2. Алгоритм Белмана-Форда

Выполним этот алгоритм для такого же графа.

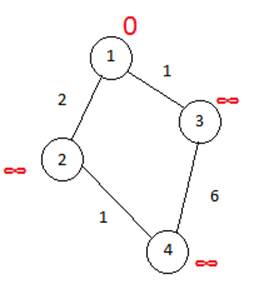
Для каждой вершины, смежной с вершиной 1, будем посчитывать кротчайший путь, то есть вес вершины 2 станет равным 2, вес вершины 1 – 1. Проделаем это действие с каждой вершиной кроме последней. И получим следующие значения весов:

Суть данного алгоритма, что он допускает наличие отрицательных весов, в отличие от алгоритма Дейкстры. Для этого достаточно проверить, если при исполнении последней итерации длина кратчайшего пути до какой-либо вершины строго уменьшилась, то в графе есть отрицательный цикл.

Код программы:

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Text;

using System.Windows.Forms;

using System.IO;

namespace l2

{

public partial class Form1 : Form

{

public Form1()

{

InitializeComponent();

label2.Visible = false;

dataGridView1.Visible = false;

button2.Visible = false;

button3.Visible = false;

groupBox1.Visible = false;

алгоритмыToolStripMenuItem.Visible = false;

dataGridView3.RowCount = 1;

dataGridView4.RowCount = 1;

}

Graf graf;            

private void обходВШиринуToolStripMenuItem_Click_1(object sender, EventArgs e)

{            //обход в ширину BFS

graf.Obhod_BFS(Int32.Parse(numericUpDown3.Value.ToString()));

dataGridView2.RowCount = graf.PUTH_L.Length;

for (int i = 0; i < graf.PUTH_L.Length; i++)

{

dataGridView2[0, i].Value = graf.PUTH_L[i];

}           

}

private void button1_Click(object sender, EventArgs e)

{           //ввод данных из файла

InPut();

dataGridView1.Visible = true;

button2.Visible = true;

label2.Visible = true;

dataGridView1.Columns[0].Width = 30;

dataGridView1.Columns[1].Width = 30;

dataGridView1.Columns[2].Width = 50;

}

private void button2_Click(object sender, EventArgs e)

{           //создание графа

button3.Visible = true;

int[,] matr = new int[dataGridView1.RowCount, dataGridView1.ColumnCount];

for (int i = 0; i < dataGridView1.RowCount; i++)

{

for (int j = 0; j < dataGridView1.ColumnCount; j++)

matr[i, j] = Int32.Parse(dataGridView1[j, i].Value.ToString());

}

graf = new Graf(dataGridView1.RowCount, dataGridView1.RowCount, matr);

}

public void InPut()

{   //чтение информации о связанных вершинах из файла

StreamReader f = new StreamReader("1.txt");

int i = 0;

string s = f.ReadLine();

string[] ss = s.Split();

dataGridView1.RowCount = Int32.Parse(ss[1].ToString());

// dataGridView1.ColumnCount = 3;

s = f.ReadLine();

while (s != null)

{

ss = s.Split();                        

dataGridView1[0, i].Value = ss[0];

dataGridView1[1, i].Value = ss[1];

dataGridView1[2, i].Value = ss[2];

i++;    

s = f.ReadLine();

}

}

private void button3_Click(object sender, EventArgs e)

{

алгоритмыToolStripMenuItem.Visible = true;

}

private void обходВГлубинуToolStripMenuItem_Click_1(object sender, EventArgs e)

{   //обход в глубину рекурсивный DFS

graf.Obhod_DFS_REKURS(Int32.Parse(numericUpDown3.Value.ToString()));

dataGridView2.RowCount = graf.PUTH_F.Length;

for (int i = 0; i < graf.PUTH_F.Length; i++)

{

dataGridView2[0, i].Value = graf.PUTH_F[i];

}

}

int[] f;

private void обходВГлубинуНерекурсивныйToolStripMenuItem_Click_