МИНИСТЕРСТВО ОБРАЗОВАНИЯ
РЕСПУБЛИКА БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ ИМЕНИ П.О.СУХОГО
Факультет автоматизированных информационных систем
Кафедра: информационные технологии
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №5
по дисциплине: конструирование программ и языки программирования
Выполнил: студент гр. ИТ-32
Принял: преподаватель
Гомель 2013
ЛАБОРАТОРНАЯ РАБОТА №5
Поcтроение максимального потока и максимального паросочетания
Цель: Изучение основных алгоритмов построение максимального потока
Задание: Реализовать алгоритмы поиска максимального потока (Эдмонсона-Карпа, Динницы).
Вариант 19
Дано: количество вершин – 8, количество ребер – 8.
Список ребер и их вес. 6 в 1 весом 2, 1 в 7 весом 1, 7 в 5 весом 2, 5 во 2 весом 2, 1 в 2 весом 3, 2 в 8 весом 2, 8 в 3 весом 3,8 в 4 весом 4.
Алгоритм Диница: Можно показать, что каждый раз количество
рёбер в блокирующем потоке увеличивается хотя бы на одно, поэтому в алгоритме
не более 
блокирующих потоков, где 
— количество вершин в сети.
Вспомогательная сеть 
может быть построена обходом в
ширину за
время 
, а блокирующий
поток на каждом уровне графа может быть найден за время 
. Поэтому время работы алгоритма
Диница есть 
.
Алгоритм Эдмондса — Карпа: В процессе работы алгоритм
Эдмондса — Карпа будет находить каждый дополняющий путь за время 
. Ниже мы докажем, что общее число
увеличений потока, выполняемое данным алгоритмом, составляет 
. Таким образом, сложность
алгоритма Эдмондса — Карпа равна 
.
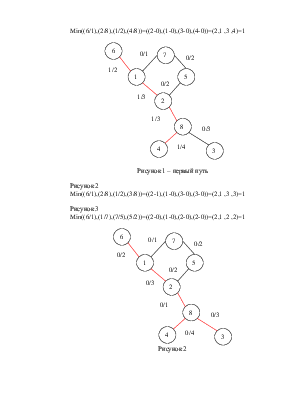
Граф можно представить, как показано на рисунке.
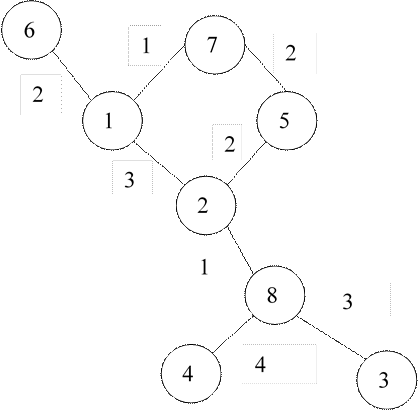
Для начала сделаем матрицу весов:
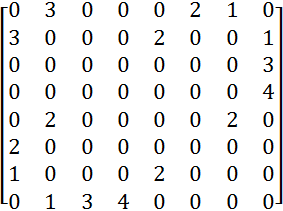
Алгоритм Эдмонсона-Карпа
1 Очередь состоит из единственной вершины 6. Посещена вершина 6, предков нет.
2 Очередь состоит из вершины 1. Посещена вершина 6 и 1. Вершина 1 имеет предка 6.
3 Очередь состоит из 7 и 2, посещены вершины 6, 1, 7, 2. Вершины 7 и 2 имеют предка 1, вершина 1 имеют предка 6.
4 Очередь состоит из 5. Посещаем 6,1,7,2 и 5. Вершина 5 имеет предка 2.
5 Очередь состоит из 8. Посещаем 6, 1, 7, 2, 5, 8. Вершина 8 имеет предка 2.
6 Очередь состоит из 4 и 3. Посещаем все остальные и вершины 3 и 4 имеют предка 8.
7 Идем по предкам: 8, 2, 1 ,6
Пропускная способность пройденного пути
Рисунок 1
Min((6/1),(2/8),(1/2),(4/8))=((2-0),(1-0),(3-0),(4-0))=(2,1 ,3 ,4)=1
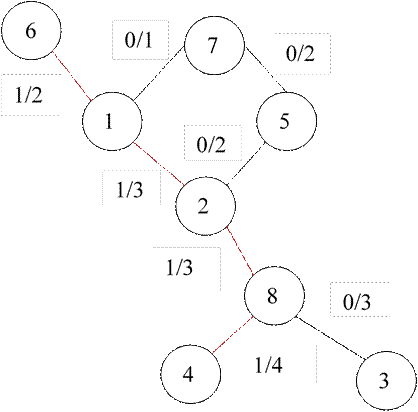
Рисунок 1 – первый путь
Рисунок 2
Min((6/1),(2/8),(1/2),(3/8))=((2-1),(1-0),(3-0),(3-0))=(2,1 ,3 ,3)=1
Рисунок 3
Min((6/1),(1/7),(7/5),(5/2))=((2-0),(1-0),(2-0),(2-0))=(2,1 ,2 ,2)=1
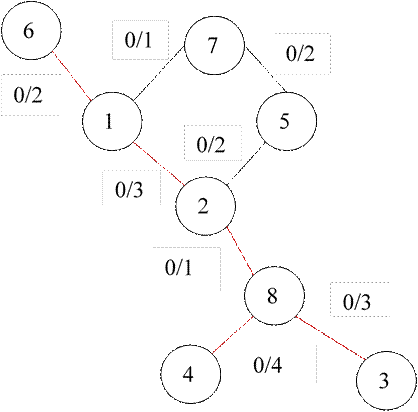
Рисунок 2
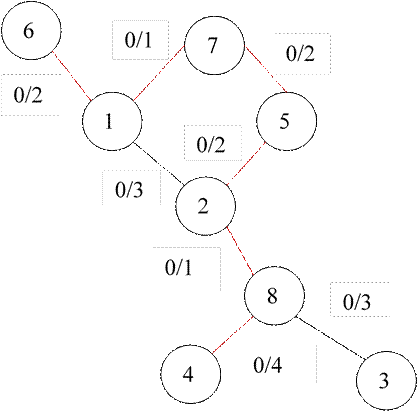
Рисунок 3
Листинг программы:
using System;
using System.Collections.Generic;
using System.Linq;
using System.IO;
using System.Text;
namespace ConsoleApplication1
{
class Program
{
public static int[,] matrica_vesa, q;
public static int kolichestvo_vershin = 8;
public static int s, t;
public static int[] mar;
public static int[] pt, massiv_proidennih_vershin, massiv_obchoda_bfs, r;
static void Main(string[] args)
{
StreamReader file = new StreamReader("test.txt");
int i = 0;
string stri = file.ReadLine();
string[] st = stri.Split();
matrica_vesa = new int[8, 8];
q = new int[8, 8];
pt = new int[8];
massiv_proidennih_vershin = new int[8];
mar = new int[8];
massiv_obchoda_bfs = new int[8];
r = new int[8];
while (stri != null)
{
st = stri.Split();
for (int j = 0; j < 8; j++)
matrica_vesa[i, j] = Int32.Parse(st[j]);
i++;
stri = file.ReadLine();
}
//Обнуляем все потоки
for (i = 0; i < 8; i++)
{
for (int j = 0; j < 8; j++)
{
q[i, j] = 0;
}
mar[i] = 0;
}
int ch=0;
do
{
Console.Clear();
Console.WriteLine("Выбор действия:");
Console.WriteLine("1. Нахождения максимального потока Эдмонсона-Карпа");
Console.WriteLine("2. Нахождения максимального потока Диница");
Console.WriteLine("3. Выход");
ch = Int32.Parse(Console.ReadLine());
switch (ch)
{
case 1:
{
int v = 0;
int t = 0;
int[] pred = new int[8]; // массив вершин
for (i = 0; i < 8; i++)
{
for (i = 0; i < 8; i++)
{
pred[i] = -1;// отмечаем как посещенную
r[i] = 0;
}
int h = 0;
t = 0;
r[t++] = 0;
pred[0] = 0;// удаляем первую в массиве
//В остаточной сети находим кратчайший путь из источника в сток.
//Если такого пути нет, останавливаемся.
for (int cur; h < t; )
{
cur = r[h++];
for (v = 0; v < 8; v++)
if (pred[v] == -1 && matrica_vesa[cur, v] - q[cur, v] > 0)
{
r[t++] = v;
pred[v] = cur;
}
}
if (pred[8 - 1] == -1)
break;
//Пускаем через найденный путь максимально возможный поток:
int min = int.MaxValue;
for (int c = 8 - 1; c != 0; )
{
//ищем ребро с минимальной пропускной способностью
int preview = pred[c];
min = Math.Min(min, matrica_vesa[preview, c] - q[preview, c]);
c = preview;
}
//Для каждого ребра на найденном пути увеличиваем поток на min, а в противоположном ему — уменьшаем на min.
for (int c = 8 - 1; c != 0;)
{
int preview = pred[c];
q[preview, c] += min;
q[c, preview] -= min;
c = preview;
}
}
//вычисляем новую пропускную способность
int d = 0;
for (i = 0; i < 8; i++)
d += q[0, i];
Console.Write("Максимальный поток при расчете методом Эдмонсона-Карпа = " + d);
Console.ReadKey();
}
break;
case 2:
{
s = 0;
t = 7;
// создаем подграф
for (i = 0; i < 8; i++)
{
for (int j = 0; j < 8; j++)
{
q[i, j] = 0;
}
}
int d = 0;
while (true)
{
if (!bfs())
break;
int p;
while ((p = dfs(s, int.MaxValue)) != 0)
d += p;
}
Console.Write("Максимальный поток при расчете методом Диница = " + d);
Console.ReadKey();
}break;
default:
break;
}
}
while (ch != 3);
}
/// <summary>
/// Поиск в глубину
/// </summary>
/// <param name="v"></param>
/// <param name="flow"></param>
/// <returns></returns>
public static int dfs(int v, int flow)
{
if (flow == 0)
return 0;
if (v == t)
return flow;
for (int to = v; to < 8; to++)
{
//ищем ребро с минимальной пропускной способностью
if (massiv_proidennih_vershin[to] != massiv_proidennih_vershin[v] + 1)
continue;
int result = dfs(to, Math.Min(flow, matrica_vesa[v, to] - q[v, to]));
if (result != 0)
{
q[v, to] += result; // увеличиваем поток и противоположный уменьшаем
q[to, v] -= result;
return result;
}
}
return 0;
}
/// <summary>
/// Поиск в ширину
/// </summary>
/// <returns></returns>
public static bool bfs()
{
int qh = 0, qt = 0;
massiv_obchoda_bfs[qt++] = s;
for (int i = 0; i < massiv_proidennih_vershin.Length; i++)
massiv_proidennih_vershin[i] = -1;
massiv_proidennih_vershin[s] = 0;
while (qh < qt)
{
int v = massiv_obchoda_bfs[qh++];
for (int to = 0; to < 8; to++)
if (massiv_proidennih_vershin[to] == -1 && q[v, to] < matrica_vesa[v, to])
{
massiv_obchoda_bfs[qt++] = to;
massiv_proidennih_vershin[to] = massiv_proidennih_vershin[v] + 1;
}
}
return massiv_proidennih_vershin[t] != -1;
}
}
}
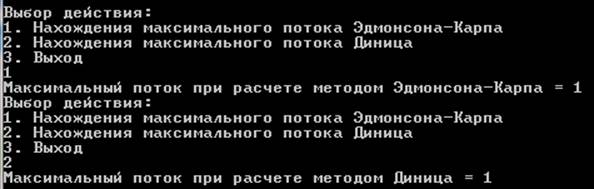
Вывод: В ходе работы изучила основные алгоритмы построения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.