Численные методы решения ОДУ и систем ОДУ. Метод последовательных приближений. Метод конечных разностей

одномерные(имеют 1 вход-1 выход) и многомерные(имеют суммарное число входов и выходов ≥2), с сосредоточенны-ми и распределенными параметрами.

В динамических моделях одним из параметров является время и выходными параметрами является функция(перемещение, ускорение,скорость) от времени.

Время:

физическое (астрономическое ), математическое (абсолютное) – без конкретной привязки к чему-либо внешнему, непрерывное, дискретное – возрастающая последовательность вида {t1,t2,…,t3}.

Графики функций x(t),y(t),z(t) – временные диаграммы.

С позиций классической физики наше пространство рассматривается как трехмерное, однородное и изотропное, не зависящее от находящихся в нем материальных тел. Ньютон подразумевал два вида пространства: относительное, с которым люди встречаются путем измерения пространственных соотношений между телами, и абсолютное - пустое вместилище тел, трехмерное евклидово пространство.

4.  Формы представления  динамических моделей.

Динамическая модель может быть представлена в следующих формах:

–  Явная функция, зависящая от времени   z=z(t)

–  Нелинейное алгебраическое уравнение относительная переменных явно зависящих от времени    G(z(t),t)=0

–  ДУ или система

–  Алгебраическое ДУ

–  Интегро-диф. уравнение или система

–  Передаточная функция

Метод реализации – с использование подстановочной функции :

5.  Виды внешних воздействий, выходные параметры динамических моделей.

Виды внешних воздействий:

-Непрерывные(функция непрерывного аргумента)

-Дискретные

-Детерминированные

-Случайные

-Одномерные

-Многомерные

Входные воздействия описываются различными функциями, в том числе и обобщенными. Выделяют 3 типа воздействия: импульсивное, единичная ступенчатая функция, гармоническое воздействие.

Функция Хэвизайда(ступенчата) имеет значение 0 для отрицательных и 1 для положительных аргументов.

- функция Дирака(импульсная) позволяет записать пространственную плотность физической величины.

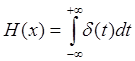
Гармоническое воздействие – явление периодического изменения какой-либо величины

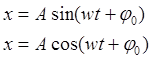
6.  Формы представления динамических моделей, примеры.

Смотрите 4 вопрос.

7.  Задачи моделирования  динамических систем.

Для динамических систем ставятся четыре группы задач:

- Задачи анализа

-Задачи синтеза(по желаемому выходному сигналу найти входной сигнал и оператор системы)

-Задачи идентификации(по заданному входному и выходному сигналам найти оператор системы)

-Обратные задачи(получить входной сигнал по заданному выходному сигналу и оператору системы)

Для динамических моделей можно проводить следующие виды анализа выходного сигнала:

-Влияние изменений начальных условий на выходной сигнал.

-Влияние изменений внутри параметров на выходной сигнал

- Влияние изменения параметров возмущающих воздействий на выходной сигнал

Для линейных динамических систем ставятся следующие задачи анализа:

-Анализ выходных процессов

 – Анализ устойчивости

– Анализ чувствительности

– Анализ управляемости

8  Передаточная функция, ее получение для динамических моделей.

Передаточная ф-ция-способ мат описания динам модели.

Передаточная ф-цияпредставл диф. оператор, выражающий связь между входом и выходом системы. Зная вх сигнал системы и передаточную ф-ию, можно восстановить вых сигнал.

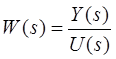Пусть U(t) – входной сигнал, а y(t) – её выходной сигнал. Тогда передаточная функция W(s) такой системы записывается в виде:

Где U(s) и Y(s) – преобразования Лапласа для сигналов u(t) и y(t) соответственно.

Получить передаточную ф-ию для механической системы по виду ДУ.

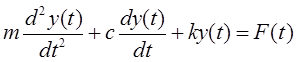Выполним преобразование Лапласа

m·S²·Y(s)+c·s·Y(s)+k·Y(s)=Z(s)        

Находим передаточную функцию

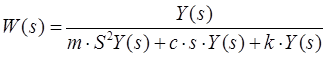
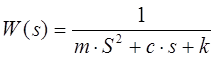9        Исследование динамических моделей в Matlab

1)  Определить ф-ю входного воздействия F(t)

2)  Выполнить преобразования Лапласа над функцией F(t)

3)  Задать передаточную функцию W

4)  Получить операторное изображение выходной функции системы, умножив операторное изображение входной функции на передаточную функцию:

5)  Выполнить выходной функцией обратное преобразование Лапласа, и получить функции выходного сигнала во временной области.

(дополнение вопрос 7, но особо не надо=))

10  Исследование переходных процессов в Matlab, общие положения