Проектирование железобетонных конструкций многоэтажного промышленного здания, страница 4

Q_max=(0,2×24,039+0,2752×52,155039)×6,5= 124,54 кН;

Q_min=(0,2×24,039-0,0752×52,15556)× 6,4= 223,775= 5,75 кН;

x/1=0,4

M_max=(0,08×24,039+0,1×52,155)× 6,4²5²= 301,6 кН×м;

M_min=(0,08×24,039-0,02×52,155)× 6,4²5²= 37,18 кН×м;

Q_max=(0×24,039+0,1496×52,155)× 6,4= 223,775= 50,71 кН;

Q_min=(0×24,039-0,1496×52,155)× 6,4= 223,775= -50,71 кН;

x/1=0,6

M_max=(0,06×24,039+0,09×52,155)× 6,4²5²= 259,25 кН×м;

M_min=(0,06×24,039-0,03×52,155)× 6,4²5²= -4,27 кН×м;

Q_max=(-0,2×24,039+0,0694×52,155)× 6,4= 223,775= -7,72 кН;

Q_min=(-0,2×24,039-0,2694×52,155)× 6,4= 223,775= -122,58 кН;

x/1=0,8

M_max=(0×24,039+0,0402×52,1556)× 6,4²5²= 88,58 кН×м;

M_min=(0×24,039-0,0402×60,56)× 6,4²5²= -88,58 кН×м;

Q_max=(-0,4×24,039+0,028×52,155)× 6,4= 223,775= -53 кН;

Q_min=(-0,4×24,039-0,428×52,155)× 6,4= 223,775= -207,6 кН;

x/1=1

M_max=(-0,1×24,039+0,0167×52,155)× 6,4²5²= -64,76 кН×м;

M_min=(-0,1×24,039-0,1167×52,155)× 6,4²5²= -358,71 кН×м;

Q_max=(-0,6×24,039+0,0167×52,155)× 6,4= 223,775= -88,09 кН;

Q_min=(-0,6×24,039-0,6167×52,155)× 6,4= 223,775= -302,81 кН;

Второй пролет

x/1=1

Q_max=(0,5×24,039+0,5833×52,155)× 6,4= 223,775= 275,87 кН;

Q_min=(0,5×24,039-0,0833×52,155)× 6,4= 223,775= 49,88 кН;

x/1=1,1

M_max=(-0,055×24,039+0,0151×52,1556)× 6,4²5²= -22,58 кН×м;

M_min=(-0,055×24,039-0,0701×52,155)× 6,4²5²= -210,33 кН×м;

Q_max=(0,4×24,039+0,487×52,155)× 6,4= 223,775= 227,59 кН;

Q_min=(0,4×24,039-0,087×52,155,56)× 6,4= 223,775= 33 кН;

x/1=1,3

M_max=(0,005×24,039+0,055×52,155)× 6,4²5²= 126,27 кН×м;

M_min=(0,005×19,28-0,05×52,155)× 6,4²5²= -105,09 кН×м;

Q_max=(0,2×24,039+0,321×52,155)× 6,4= 223,775= 140кН;

Q_min=(0,2×24,039-0,121×52,155)× 6,4= 223,775= -9,77 кН;

x/1=1,5

M_max=(0,025×24,039+0,075×52,155)× 6,4²5²= 190,65 кН×м;

M_min=(0,025×24,039-0,05×52,155)× 6,4²5²= -84,78 кН×м;

Q_max=(0×24,039+0,1979×52,155)× 6,4= 223,775= 67,09 кН;

Q_min=(0×24,039-0,1979×52,155)× 6,4= 223,775= -67,09 кН;

По найденным усилиям строятся огибающие эпюры М и Q (рис. 9).

4.4. Расчет по прочности нормальных сечений

Уточняем высоту сечения ригеля по наибольшему по модулю изгибающему моменту на опоре B M_B=368,45 кН×м.

Определяем изгибающий момент, действующий по грани колонны

 кН×м.

где Q – поперечная сила на опоре В справа;

 h_к – высота сечения колонны в направлении пролета ригеля; h_к=0,3 м.

При ширине ригеля b=250 мм; x=0,35; A₀=x(1-0,5x)=0,289 рабочая высота ригеля

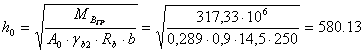 мм.

Полная высота сечения ригеля при двухрядном расположении по высоте сечения стержней продольной арматуры

h=h₀+a=580.13+70=650.13 мм.

С учетом требовании унификации высоту сечения ригеля округляем в большую сторону до размера, кратного 50 мм, т. е. h=700 мм.

Отношение  находится в пределах оптимальных значений. Тогда

h₀=h-a=700-70=630 мм.

Требуемую площадь сечения продольной арматуры в расчетных сечениях ригеля (см. рис. 8, а) определяем как для элемента прямоугольного сечения с одиночной арматурой. Результаты подбора арматуры сведены в табл. 2.

Поскольку площадь сечения продольной рабочей арматуры одного горизонтального ряда существенно отличается от площади сечения арматуры другого горизонтального ряда, находим положение центра тяжести для всей рабочей арматуры относительно оси, проходящей через центры тяжести стержней крайнего ряда. Для этого вычисляем статический момент площади рабочей арматуры относительно этой оси, который делим на площадь сечения арматуры:

 мм.

После этого определяем уточненное значение h₀

h₀=h-(y+a₁),

где a₁ – принятая толщина защитного слоя бетона плюс половина диаметра рабочей арматуры.

h₀=650-(15+45)=650 мм.

Аналогичным образом получаем:

для сечения II—II y=23 мм; h₀=640 мм;

для сечения III—III y=13 мм; h0=644 мм.

4.5. Построение эпюры материалов

1. Определяем изгибающие моменты, воспринимаемые в сечениях ригеля при фактически принятой продольной арматуре. При этом используются размеры, приведенные в табл. 2.

Первый пролет. Арматура 2 Æ28+2 Æ18 (A_s=1741 мм²); h₀=590 мм.

;

;

 кН×м.

Обрываем верхние два стержня  Æ18 мм и оставляем два стержня  Æ28 мм (A_s=1232 мм²); h₀=605 мм.

; ;

 кН×м.

Опора Б. Арматура 2 Æ28+2 Æ20 (A_s=1860 мм²); h₀=585 мм.

; ;

 кН×м.

Обрываем верхние два стержня  Æ20 мм и оставляем два стержня  Æ28 мм (A_s=1232 мм²); h₀=605 мм.

; ;

 кН×м.

Заменим на части пролета 2 Æ28 на 2 Æ14 (A_s=308 мм²); h₀=605 мм.

; ;

 кН×м.

2. Места расположения точек теоретического обрыва рабочих стержней определяем графически путем совмещения ступенчатой эпюры материалов с огибающей эпюрой момен­тов от внешних нагрузок (см. рис. 9). Точки теоретического обрыва рабочих стержней совпадают с точками пересечения огибающей эпюры моментов с горизонтальными линиями эпюры материалов.

3. Определяем длину анкеровки обрываемых стержней

,

где Q – поперечная сила в точке теоретического обрыва стержня, соответствующая тому сочетанию нагрузок, при котором в этом сечении получено наибольшее по величине значение изгибающего момента;

d – диаметр обрываемого стержня;

 – усилие на 1 мм, воспринимаемое поперечными стержнями на участке заделки;

A_sw – площадь сечения поперечных стержней, расположенных в одной нормальной к продольной оси элемента плоскости;

s – шаг поперечных стержней на участке заделки;

R_sw=175МПа – расчетное сопротивление поперечной арматуры.

В зависимости от наибольшего диаметра продольных стержней из условии сварки назначаем диаметр поперечных стержней d_w=8 мм (d_sw=50,24 мм²). Число плоских каркасов n=2, при этом площадь поперечных стержней, расположенных в одной, нормальной к продольной оси элемента плоскости, пересекающей наклонное сечение A_sw=n×d_sw=2×50,24=101мм².