Решение дифференциальных уравнений и систем в MathCad. Решение дифференциальных уравнений первого порядка

4. Решение дифференциальных уравнений  и систем  в

MathCad

4.1. Решение дифференциальных уравнений первого порядка

Для решения  дифференциальных уравнений   с начальными условиями  система Mathcad имеет ряд встроенных функций:

rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;

Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;

Odesolve – функция, решающая ОДУ блочным методом.

Ниже приведено описание стандартной функции rkfixed с указанием параметров функции.

rkfixed(y, x1, x2, p, D)

Аргументы функции:

y – вектор начальных условий из k элементов (k – количество уравнений в системе);

x1 и x2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;

p – число точек внутри интервала (x1, x2), в которых ищется решение;

D – вектор, состоящий из k-элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.

Результатом работы функции  является  матрица из p+1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.

Стандартная функция Odesolve имеет следующий общий вид:

Odesolve(x, n) или

Odesolve(v, x, n)

Аргументы функции следующие:

·  n – правая граница интервала, на котором ищется решение дифференциального уравнения;

·  х – переменная, относительно которой ищется решение ОДУ;

·  v – вектор имен функций при решении систем дифференциальных уравнений.

Левая граница интервала определяется из начальных условий.

В результате работы Odesolve формируется функция, являющаяся решением дифференциального уравнения относительно аргумента х. При решении ОДУ и систем ОДУ с помощью функции Odesolve необходимо организовать решающий блок по аналогии с решающим блоком для решения систем алгебраических уравнений.

Последовательность решения такова:

·  задается ключевое слово Given (начало решающего блока);

·  задается вид дифференциального уравнения, причем знак производной можно задать с помощью клавиш Ctrl-F7, а знак равенства – с помощью кнопки логического равенства на палитре знаков логических операций;

·  задаются начальные условия, для чего используется знак логического равенства;

·  задается функция Odesolve с параметрами, формируется результирующая функция.

Все вычислительные блоки, расположенные между зарезервированными словами Given и Odesolve, называются решающим блоком для решения дифференциальных уравнений и систем.

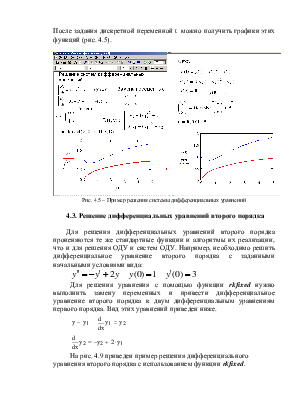
На рис. 4.1 приведен конкретный пример решения дифференциального уравнения первого порядка в MathCAD с помощью различных стандартных функций. Ниже приведено краткое описание этого примера.

При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y₁, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixedуказывается имя вектора Y,  границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D.

В результате получается матрица z, в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.

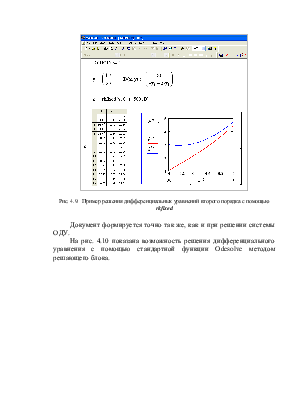
При решении с помощью функции Odesolve создается решающий блок, в котором описывается само уравнение и начальное условие для его решения в естественном математическом виде. Затем формируется результирующая функция y (она задается только своим именем) путем обращения к функции Odesolve с параметрами х – переменная, относительно которой ищется решение ОДУ, 2 – конечное значение интервала изменения этой переменной. Результирующее значение функции у(х) представлено в виде графика, причем х необходимо описать как дискретную переменную.

4.2 Решение систем дифференциальных уравнений

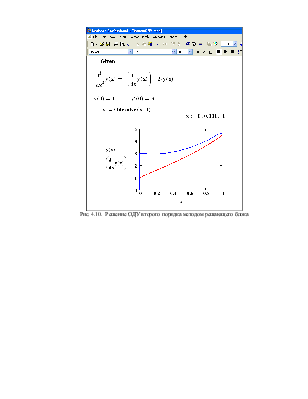
Системы дифференциальных уравнений можно решать как с помощью функцииrkfixed так и с помощью Odesolve. При решении системы дифференциальных уравнений с помощью функции