Некоторые линейные модели экономики. Динамика рыночных цен. Основные количественные параметры рынка, страница 2

Моделированию коррекции цены и спроса на неравновесном рынке посвящен этот раздел. Для простоты аналитического исследования функции спроса и предложения будут предполагаться линейными, поэтому и модели называются линейными.

Предварительно решим в форме примера необходимую вспомогательную задачу. В ней понадобится дать еще один вид аналитического представления прямой.

П р и м е р  26.  Ф у н к ц и и л и н е й н о г о с п р о с а и п р е д л о ж е н и я в     р а в н о в е с н о й  ф о р м е.

1. написать уравнение с угловым коэффициентом k ¹ 0 относительно оси Ox и коэффициентом l ¹ 0 относительно оси Oy прямой, проходящей через точку , где

2. Записать линейные функции спроса и предложения в равновесной форме.

Р е ш е н и е:  1.  Если точка  лежит на прямой, заданной уравнением y = kx + b, то  откуда . Подставляя b, получаем

Это уравнение можем переписать в виде С другой стороны, уравнение с угловым коэффициентом относительно оси Oy имеет вид x = ly + c, где , откуда  - уравнение той же прямой, следовательно, l = k^-1.

Итак, искомые уравнения имеют вид

2. Поскольку функция предложения Q = S(P) - возрастающая, то, считая угловой коэффициент у оси OP равным s > 0, получим

Q = S(P) = Q_e + s (P - P_e). функция спроса Q = D(P) убывает и также проходит через точку равновесия (Q_e, P_e), следовательно,

Q = D(P) = Q_e - d (P - P_e).

где (-d) - угловой коэффициент (d > 0) функции спроса к оси OP.

Теперь обратимся к самим моделям.

1. Модель с запаздыванием спроса (модель А). Идея этой модели заключается в том, что субъект рынка (или рынок в целом) по текущей неравновесной цене определяет уровень предложения товара, а затем предлагает новую цену, для которой спрос равняется найденному уровню предложения.

Модель точно формулируется следующим образом. Время t предполагается дискретным: t = 1, 2, ... Линейное предложение Q = S(P) = Q_e + s (P - P_e) и спрос Q = D(P) = Q_e - d (P - P_e).

1.  S_t+1 = S(P_t).

2. В каждый следующий момент времени цена определяется равенством

D(P_t+1) = S_t+1 = S(P_t).

Тогда, согласно уравнениям в равновесной форме имеем

D(P_t+1) = Q_e - d (P_t+1 - P_e) = Q_e + s (P_t - P_e) = S(P_t).

Следовательно, P_t+1 - P_e =. Отсюда получаем P_t+1, далее по P_t+1 согласно правилам 1 и 2 находим P_t+2 и т.д.

Смысл этой последовательной коррекции - привести цену и количество рассматриваемого товара к равновесию, чтобы удовлетворить спрос и избежать товарных излишков. Всегда ли эта цель достигается? Положим . Имеем y₂ = qy₁, y₃ = qy₂ = q²y₁,..., y_n+1 = qⁿy₁, где q = s / d, значит, (y_n)_n³1 - геометрическая прогрессия, которая сходится только при q < 1 и имеет предел 0. Условие q < 1 равносильно условию s < d.

Графически этот процесс изображен на рис. 19. Для графиков условие s < d означает, что угол наклона прямой S к OP меньше острого угла p -j,

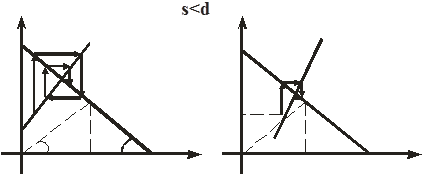
рис. 19

где j- тупой (tg j = -tg a < 0) угол прямой D с OP (меньшему тангенсу соответствует меньший угол). p - j = a - острый угол D с осью OQ;  - величина угла пунктирной прямой, выходящей из начала координат, к OP. Из обоих рисунков видно, что прямая S составляет меньший угол с OP, чем пунктирная прямая.

Альтернативные варианты (когда процесс коррекции цены не сходится) в геометрической форме представлены на рис 20. На левом графике процесс расходится, на правом  - неустойчивое равновесие.

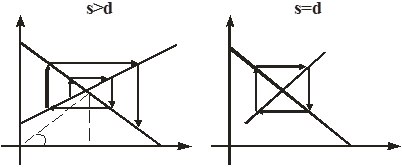
Рис. 20

В реальности спрос и предложение нелинейны, но процесс коррекции цены имеет тот же качественный характер (рис. 21).

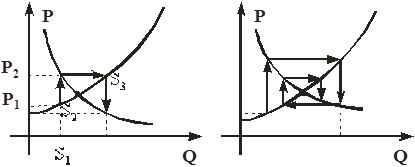
Рис. 21

2. Модель с запаздыванием предложения (модель В).

Модель точно формализуется следующим образом. Время t предполагается дискретным: t = 1, 2, ... Линейное предложение Q = S(P) = Q_e + s (P - P_e) и спрос Q = D(P) = Q_e - d (P - P_e).

1.  S_t = S(P_t), D_t = D(P_t).

2. В каждый следующий момент времени цена определяется равенством

S(P_t+1) = D_t = D(P_t).

Читателю предоставляется возможность сформулировать экономический смысл процесса коррекции и проанализировать условия сходимости к равновесию. В геометрической форме все три варианта представлены на рисунке 22.

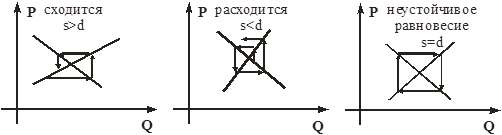
Рис. 22

Обе изложенные модели называются также паутинными (или паутинообразными) моделями Вальраса (Леон Эспри Вальрас (L. Walras, 1834 - 1910) - швейцарский экономист, в своей знаменитой работе «Elements of Pure Economics», вышедшей в Лозанне в 1874 г., изложил механизмы общего равновесия в макроэкономической модели индустриального рынка). Образный эпитет «паутинные» дан вследствие того, что геометрическая картина коррекции напоминает паутину.

В XX в. были предложены адаптивные модели, сочетающие в себе элементы обеих моделей коррекции; в них решение о следующей цене принимаются с учетом одновременно и спроса, и предложения.