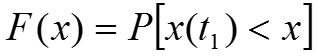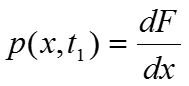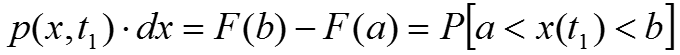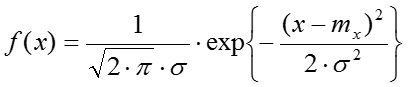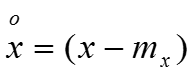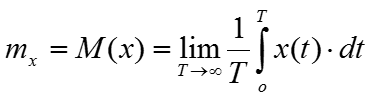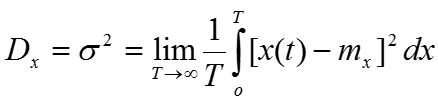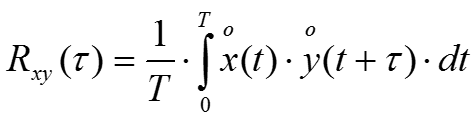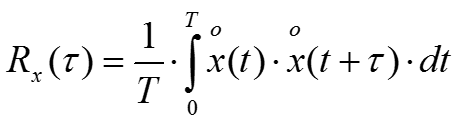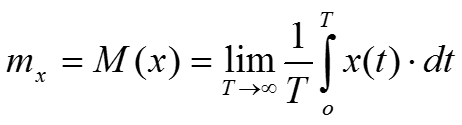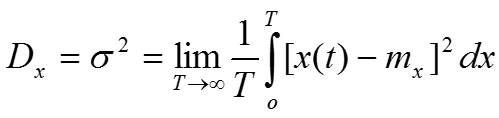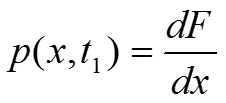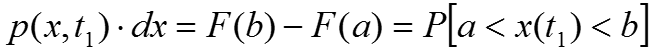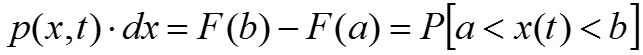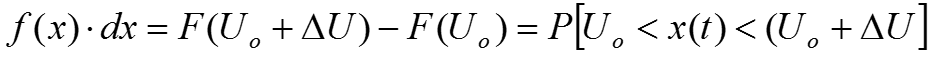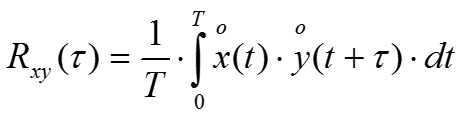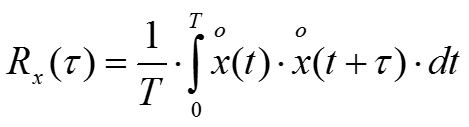Измерители законов и параметров распределения случайных величин
-
Приборы необходимы для измерения параметров случайных процессов:
-
- математического ожидания;
-
- дисперсии;
-
- Приборы для измерения отношения сигнал/шум;
-
и законов распределения случайных процессов:
-
- измерители интегральных и дифференциальных функций распределения;
-
- измерители корреляционной функции.
-
Для оценки случайного процесса требуется выполнить ряд сложных измерений и оценить:
-
Интегральную функцию
-
распределения
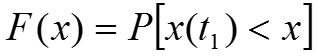
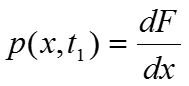
-
Одномерную плотность
-
вероятности
,
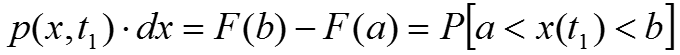
. t1 – т.к. в заданный момент времени.
Например, нормальный закон:
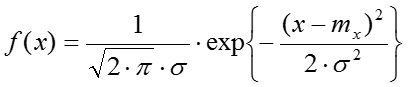
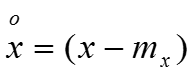
, центрированный процесс
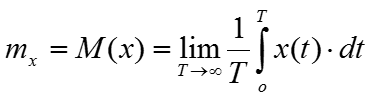
.
- Мат. ожидание
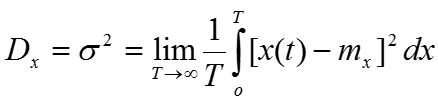
.
- Дисперсию
.
- Корреляционную функцию
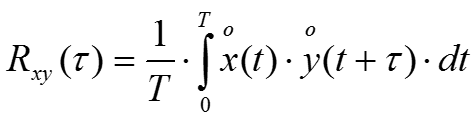
.
-Автокорреляционную функцию
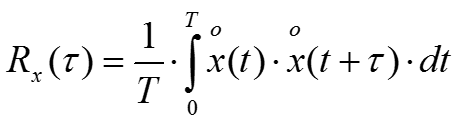
.
Измеритель математического ожидания случайного процесса
-
Для измерения мат. ожидания необходимо реализовать следующую функцию:
-
Простейший измеритель среднего значения (мат. ожидания):
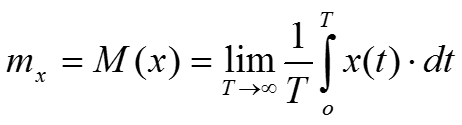
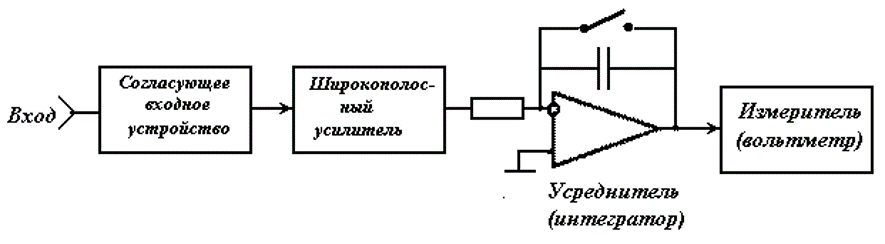
Цифровой измеритель среднего значения (математического ожидания):
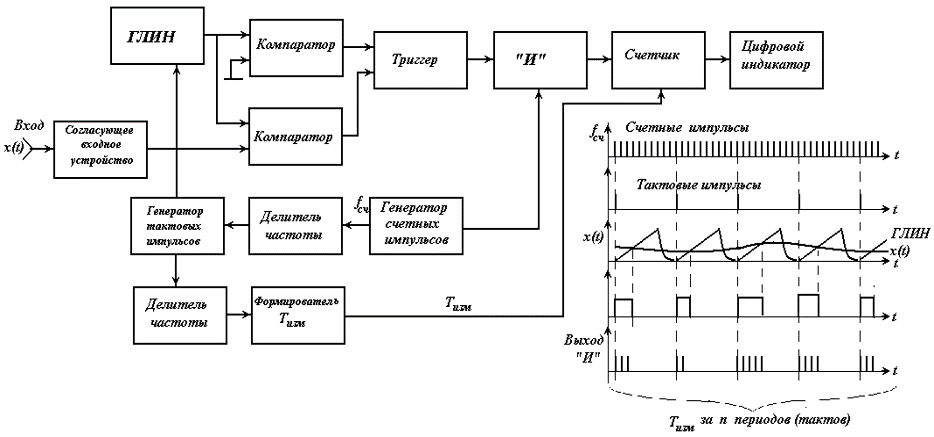
Измеритель мощности случайного процесса
-
Это обычный измеритель уровня (среднеквадратического значения напряжения).

Измеритель дисперсии
-
Для измерения дисперсии необходимо реализовать следующую функцию:
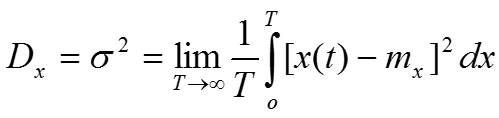
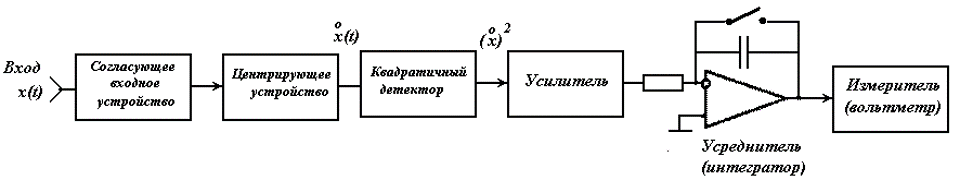
-
Для центрирования случайного процесса можно просто поставить разделительный конденсатор большой емкости.
-
Для возведения в квадрат центрированных процессов требуется устройство с большой протяженностью квадратичной характеристики. Используется аппроксимация характеристики, как в измерителях уровня (квадратичный детектор).
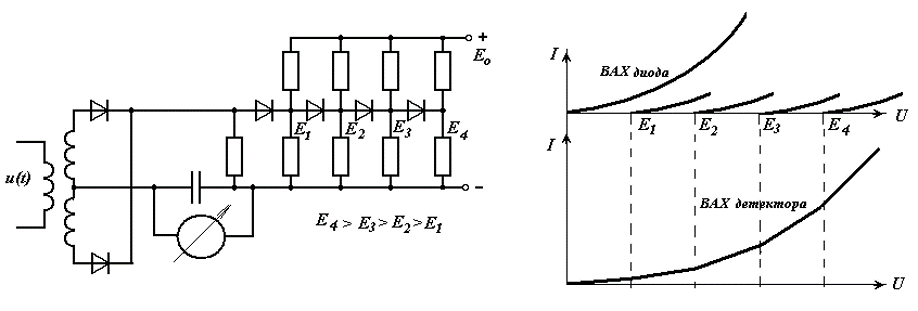
Измеритель закона распределения вероятности случайного процесса
-
Интегральная функция распределения F(x) – неубывающая функция. Входной случайный процесс сравнивается с регулируемым порогом, и измеряется в соответствии с выражением .
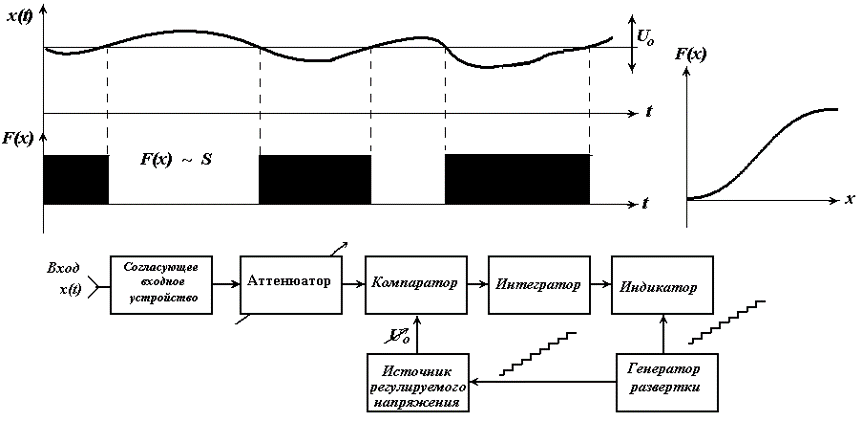
Измеритель плотности вероятности случайного процесса
-
Измеритель одномерной плотности вероятности случайного процесса работает в соответствии с выражениями:
-
Для эргодических и стационарных процессов:
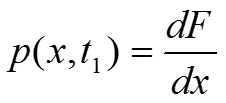
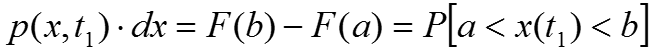
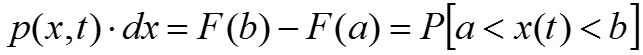
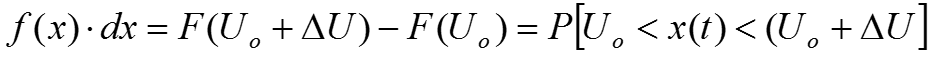
Измеритель плотности вероятности случайного процесса
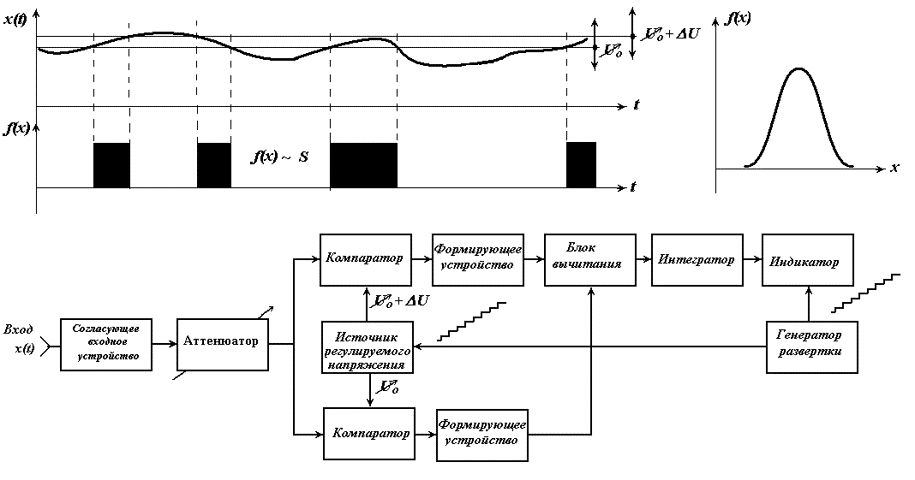
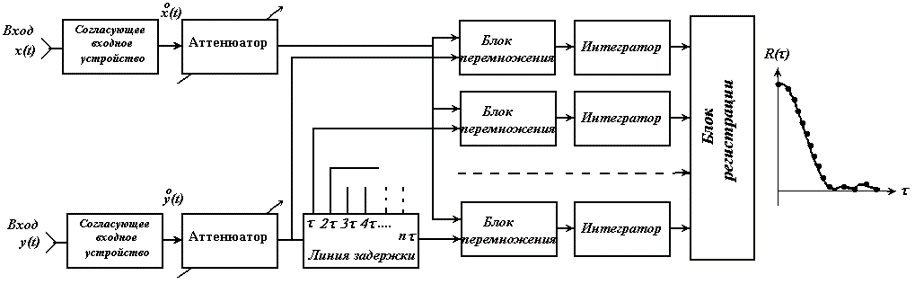
Измеритель корреляционной функции случайных процессов (коррелометр)
-
- Корреляционная функция
-
-Автокорреляционная функция
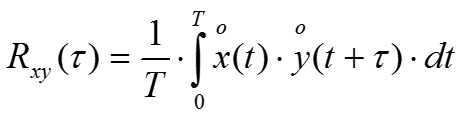
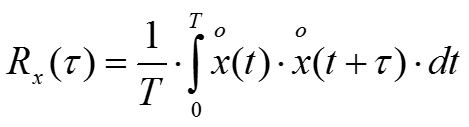
-
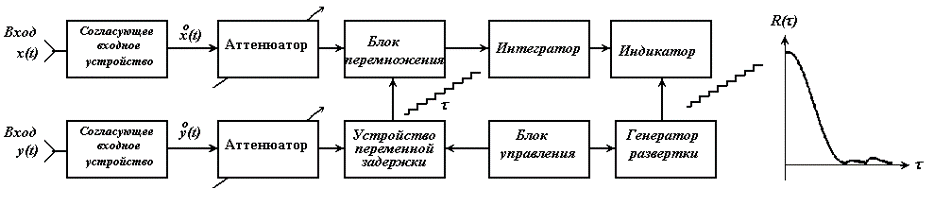
Во входном устройстве происходит центрирование случайного процесса (например, стоит разделительный конденсатор большой емкости), чтобы не измерялись моментные функции.
-
Блок перемножения выполняется:
-
- на аналоговых перемножителях, балансных модуляторах (прямые методы);
-
- на датчике Холла и др. (непрямые методы). Хуже по частотным свойствам и нелинейности.
-
В цифровых коррелометрах во входных устройствах есть еще АЦП, Δ – по Котельникову.
-
При измерении автокорреляционной функции:
-
- каждое значение перемножается само на себя (получают дисперсию);
-
- вводят задержку на τ;
-
- умножают нулевую ординату на первую;
-
- умножают первую ординату на вторую;
-
- умножают вторую ординату на третью - и т. д.;
-
- все суммируют;
-
- затем вводят задержку еще на τ (2τ) - и т.д.
Для быстродействия – параллельный коррелометр