1. ПРОГНОЗИРОВАНИЕ РАЗВИТИЯ ПРОИЗВОДСТВА.
Обоснование параметров проектирования новых лесозаготовительных предприятий на предпроектной стадии или проектирования их реконструкции, а также при проектировании технологических процессов осуществляется на основе прогнозирования развития производства. Прогнозирование чаще всего производится с использованием экстраполяционных методов, которые базируются на предположении о том, что будущее является продолжением настоящего. При этом предполагается, что в будущем, в пределах прогноза, сохраняются существующие тенденции развития.
Прогнозирование производится с использованием математических методов, таких как интерполирование, экспоненциальное сглаживание, скользящей средней, наименьших квадратов, метод Чебышева, экспертных оценок, имитационного моделирования.
1.1. Корреляционный анализ.
В процессе прогнозирования часто необходимо установить вид связи между исследуемым процессом и факторами, влияющими на него. Для этого используется теория корреляции. На основании теории корреляции по фактическому информационному материалу, собранному в процессе предварительных исследований, выявляют наличие зависимости, форму связи и тесноту связи исследуемых факторов.
Чтобы изучить характер влияния величины x на y, наблюдениями определяют значение y при разных значениях x. Если x и y связаны функциональной зависимостью, то каждому значению xсоответствует вполне определенное значение y. Если каждому значению x будет соответствовать статистический ряд возможных значений y, то связь между величинами называется статистической. Изучение связи между x и y предполагает рассмотрение распределения величины y для каждого x и изменения этого распределения от изменения x. Такое распределение можно представить таблицей, в которой указаны частоты пар значений (x,y), называемой корреляционной таблицей. В корреляционной таблице на пересечении каждого столбца и строки приведена частота mxy указывающая, сколько раз при данных значениях x встретились указанные значения y.
Для проектирования цеха первичной обработки древесины и эффективной организации производственного процесса по раскряжевке поступающих из лесосек хлыстов важно знать не только общий объем, но и количество поступающих хлыстов. Для определения количества хлыстов, поступающих на нижний склад из лесосек с известным средним объемом хлыста, выполнены исследования по определению зависимости количества хлыстов, доставляемых автопоездами с различных лесосек.
В табл. 1.1 представлены результаты обследования автопоездов, прибывающих на нижний склад ЛЗП. В этой таблице y – означает средний объем хлыста, а x– количество хлыстов в пачке. Например, число 9 в четвертом столбце второй строки означает, что автопоездов со средним объемом хлыста 0,4¸0,6 м3 встретилось 9 раз.
Таблица 1.1
Корреляционная таблица.
|
Объем хлыста. Y |
Количество наблюдений с числом хлыстов в пачке – x |
ny |
||||
|
20 – 30 |
30 - 40 |
40 – 50 |
50 – 60 |
60 – 70 |
||
|
0,2 – 0,4 |
10 |
6 |
3 |
4 |
23 |
|
|
0,4 – 0,6 |
7 |
9 |
5 |
21 |
||
|
0,6 – 0,8 |
4 |
8 |
2 |
14 |
||
|
mx |
4 |
25 |
17 |
8 |
4 |
58 |
В последней строке корреляционной
таблицы приведены частные суммы mx =
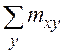 ,
а в последнем столбце – частные суммы
,
а в последнем столбце – частные суммы 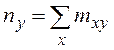
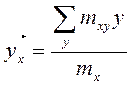 Чтобы оценить характер изменения y от
изменения x, введем условные средние y по
x:
Чтобы оценить характер изменения y от
изменения x, введем условные средние y по
x:
(1.1)
Например, для 40 < x £ 50 вид распределения y:
|
y |
0,2 – 0,4 |
0,4 – 0,6 |
0,6 – 0,8 |
|
mxy |
6 |
9 |
2 |
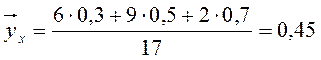 Принимая для y середины интервалов и
взвешивая их частотами, получаем
Принимая для y середины интервалов и
взвешивая их частотами, получаем
Значение условной средней `yx=f(x) следующее:
|
x |
20 - 30 |
30 – 40 |
40 – 50 |
50 – 60 |
60 – 70 |
|
y |
0,7 |
0,48 |
0,45 |
0,42 |
0,3 |
Такая связь `yx c x называется корреляционной. Основной задачей корреляционного анализа является определение функции `yy = f(x), то есть формы связи и оценка степени рассеяния y для разных x, то есть тесноты связи. Анализируя по существу природу зависимости, устанавливают характер той функции, которая выражает изменение yx в зависимости от x. Эта функция может быть линейной
![]() (1.2)
(1.2)
![]() или нелинейного вида
или нелинейного вида
(1.3)
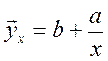 или (1.4)
или (1.4)
Коэффициенты уравнения `y = f(x), называемого уравнением регрессии, обычно находят методом наименьших квадратов.
Если связь между x и y функциональная, то вычисленные по уравнению регрессии значения y совпадут с фактическими. Но в статическом наблюдении функциональная зависимость превращается в корреляционную потому, что коэффициенты a и b , отражающие различные прочие условия, меняются от объекта к объекту. Чем больше вариации прочих условий, тем больше фактические значения y отличаются от вычисленных. Понимая под теснотой корреляционной зависимости относительное значение вариации условия x в общей вариации y, можно измерить ее коэффициентом корреляции r, который при линейной связи равен
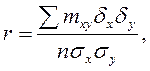 (1.5) где dx, dy – отклонение значений x и y от их общих средних M(x) и M(y),
(1.5) где dx, dy – отклонение значений x и y от их общих средних M(x) и M(y),
dx = x - M(x); dy = y – M(y);
где n – общее число наблюдений; sx, sy – среднеквадратические отклонения x и y.
Коэффициент корреляции может иметь значения от –1 до +1. Если r = ±1, то связь y с x функциональная (однозначная) и все точки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.