Установление плана производства на первые три месяца следующего периода. Прогнозирование методом наименьших квадратов.

1. Установление плана производства на первые три месяца следующего периода.

Прогнозирование методом наименьших квадратов.

Расчёты производим в программе Microsoft Excel.

a = 6; b = 98;

Эмпирическая линия регрессии y = 6t + 98;

y₁₃ = 6 ∙ 13 + 98  = 176;

y₁₄ = 6 ∙ 14 + 98  = 182;

y₁₅ = 6 ∙ 15 + 98  = 188;

Также оцениваем погрешность вычислений по методу наименьших квадратов:

S_y = 6,259;

Результаты расчета приведены в таблице на следующей странице, по данным, приведённым в таблице, построен график «Эмпирическая линия регрессии»:

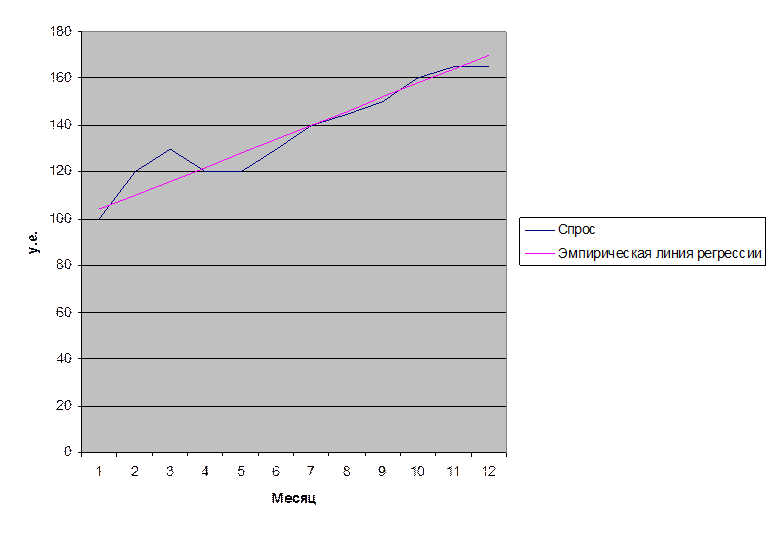
Рис.1. Эмпирическая линия регрессии.

Прогнозирование методом экспоненциального сглаживания.

;

;

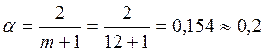y₁₃ = (1-0,2) ∙ 100 + (1-0,2) ∙ 0,2 ∙ 120 + (1-0,2) ∙ 0,2² ∙ 130 + (1-0,2) ∙ 0,2³ ∙ 120 +

+ (1-0,2) ∙ 0,2⁴ ∙ 120 + (1-0,2) ∙ 0,2⁵ ∙ 130 + (1-0,2) ∙ 0,2⁶ ∙ 140 + (1-0,2) ∙ 0,2⁷ ∙ 145 +

+ (1-0,2) ∙ 0,2⁸ ∙ 150 + (1-0,2) ∙ 0,2⁹ ∙ 160 + (1-0,2) ∙ 0,2¹⁰ ∙ 165 + (1-0,2) ∙ 0,2¹¹ ∙ 165 =

= 104,32392175616 ≈ 104;

y₁₄ = (1-0,2) ∙ 104 + (1-0,2) ∙ 0,2 ∙ 100 + (1-0,2) ∙ 0,2² ∙ 120 + (1-0,2) ∙ 0,2³ ∙ 130 +

+ (1-0,2) ∙ 0,2⁴ ∙ 120 + (1-0,2) ∙ 0,2⁵ ∙ 120 + (1-0,2) ∙ 0,2⁶ ∙ 130 + (1-0,2) ∙ 0,2⁷ ∙ 140 +

+ (1-0,2) ∙ 0,2⁸ ∙ 145 + (1-0,2) ∙ 0,2⁹ ∙ 150 + (1-0,2) ∙ 0,2¹⁰ ∙ 160 + (1-0,2) ∙ 0,2¹¹ ∙ 165 =

= 104,06478381056 ≈ 104;

y₁₅ = (1-0,2) ∙ 104 + (1-0,2) ∙ 0,2 ∙ 104 + (1-0,2) ∙ 0,2² ∙ 100 + (1-0,2) ∙ 0,2³ ∙ 120 +

+ (1-0,2) ∙ 0,2⁴ ∙ 130 + (1-0,2) ∙ 0,2⁵ ∙ 120 + (1-0,2) ∙ 0,2⁶ ∙ 120 + (1-0,2) ∙ 0,2⁷ ∙ 130 +

+ (1-0,2) ∙ 0,2⁸ ∙ 140 + (1-0,2) ∙ 0,2⁹ ∙ 145 + (1-0,2) ∙ 0,2¹⁰ ∙ 150 + (1-0,2) ∙ 0,2¹¹ ∙ 160 =

= 104,02063622144 ≈ 104;

Прогнозирование методом скользящего среднего.

Прогнозируемые точки определяются путём расчёта среднего арифметического пяти последних наблюдений:

;

;

;

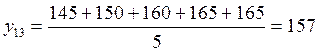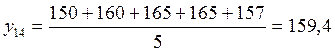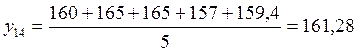Прогнозирование методом Чебышева.

Расчёты производим в программе Microsoft Excel.

Согласно применяемой формуле f₀(t) = 1

Находим многочлен f₁(t) = t – 78/12 = t – 6,5;

a₁ = -78/12 = -6,5;

a₀ = 1645/12 = 137;

Уравнение нулевой степени будет равно: y = a₀ + a₁f₁(t) = 137 + 3,05(t-6,5) = 3,05t + 117,13;

y₁₃ = 3,05 ∙ 13 + 117,13  = 156,78;

y₁₄ = 3,05 ∙ 14 + 117,13  = 159,83;

y₁₅ = 3,05 ∙ 15 + 117,13  = 162,88;

Находим многочлен f₂(t) = t² + kt + p;

b₂ = 6,5;

Y₂ = 11,92;

Многочлен будет равен f₂(t) = t² + 13t + 30,33;

Найдём a₂ = 0,156;

Многочлен второй степени будет равен:

y = a₀ + a₁f₁(t) + a₂f₂(t_i) = 137 + 3,05(t-6,5) + 0,16(t² – 13t + 30,33) = 147,47 – 0,97t + 0,16t²;

Результаты расчета приведены в таблице на следующей странице, по данным, приведённым в таблице, построен график:

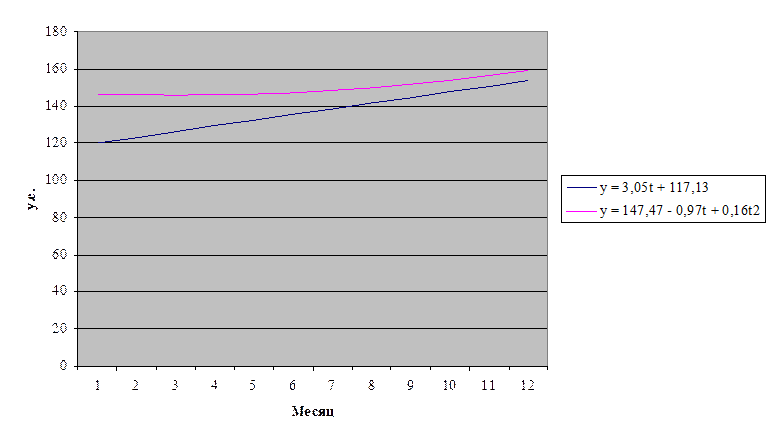
Рис.2. График построенный по результатам расчёта по методу Чебышева.