Формулировка транспортной задачи. Распределение доставки древесины. Математическая постановка задачи

Формулировка транспортной задачи.

В лесозаготовительном холдинге имеются А₁, А₂, А₃, А₄, А₅ с мощностями:

Q₁ = 250 тыс. м³;

Q₂ = 220 тыс. м³;

Q₃ = 90 тыс. м³;

Q₄ = 510 тыс. м³;

Q₅ = 410 тыс.м³;

Древесина должна быть доставлена потребителям - деревообрабатывающим предприятиям В₁, В₂, В₃, В₄, имеющим соответственно объёмы переработки:

Y₁ = 270 тыс. м³;

Y₂ = 530 тыс. м³;

Y₃ = 310 тыс. м³;

Y₄ = 370 тыс. м³;

Стоимость доставки древесины с каждого лесозаготовительного предприятия каждому перерабатывающему предприятию определяется матрицей стоимостей:

Объём заготовки древесины всеми лесозаготовительными предприятиями равен объёму потребления древесины всеми деревообрабатывающими предприятиями.

250 + 220 + 90 + 510 + 410 = 270 + 530 + 310 + 370;

Необходимо определить такое распределение доставки древесины, чтобы общая стоимость транспортных затрат была минимальной.

Математическая постановка задачи.

Целевая функция:

;

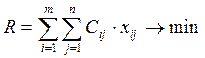При заданных условиях:

;

;

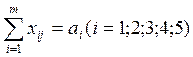Решение задачи.

Способ минимального элемента.

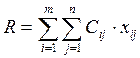 = 250 ∙ 4 + 10 ∙ 3 + 210 ∙ 4 + 70 ∙ 4 + 20 ∙ 3 +  270 ∙ 5 +  240 ∙ 7 + 270 ∙ 5 +

140 ∙ 6 = 7430 тыс. руб.;

Решение будет оптимальным только тогда, когда целевая функция примет минимальное значение.

Проверка решения на оптимальность.

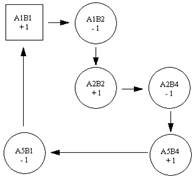       ∑С₁₁ = 9 – 4 + 3 – 4 + 3 – 6 = 1;

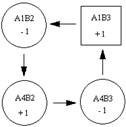                     ∑С₁₃ = 9 – 4 + 5 – 7 = 3;

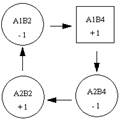                      ∑С₁₄ = 8 – 4 + 3 – 4 = 3;

                       ∑С₂₁ = 7 – 4 + 6 – 5 = 4;

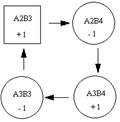                      ∑С₂₃ = 6 – 4 + 3 – 4 = 1;

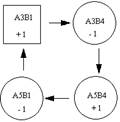                     ∑С₃₁ = 3 – 3 + 6 – 5 = 1;

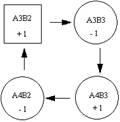                     ∑С₃₂ = 2 – 4 + 7 – 5 = 0;

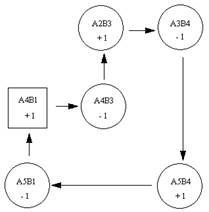   ∑С₄₁ = 6 – 7 + 4 – 3 + 6 – 5 =1;

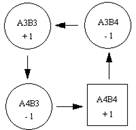                 ∑С₄₄ = 8 – 3 + 4 – 7 = 2;

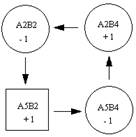                     ∑С₅₂ = 7 – 6 + 4 – 3 = 2;

                     ∑С₅₃ = 8 – 6 + 3 – 4 = 1;

В данном случае мы не имеем ни одной отрицательной характеристики цепи – следовательно, решение оптимальное.