Денежные потоки проекта в виде временной диаграммы. Анализ чувствительности инвестиционного проекта

Задание 2

Компания «АВС» рассматривает возможность производства нового вида продукции. Проект требует I₀ = 50 млн. начальных инвестиций, при этом:

- планируемый годовой выпуск продукции   Q = 16000;

- ожидаемая цена единицы продукции   р = 13000;

- переменные издержки в расчёте на одну единицу   v = 12100;

- постоянные издержки за один год   F = 4 млн.;

- налоговая ставка (налог на прибыль)   t = 30 %;

- уровень инфляции   i = 20 %;

- срок проекта   n = 4 года;

- эффективная банковская процентная ставка (норма дисконтирования) l = 12 %.

Налог на прибыль взимается в конце года с разности между прибылью за год и амортизационными отчислениями (причём только в том случае, когда разность положительна). Годовая амортизация в данной модели находится как отношение начальных инвестиций к сроку проекта. В конце k периодов капитализации ожидаемые денежные потоки составят С_k, где k = 1…n.

1. Рассчитать и представить денежные потоки проекта в виде временной диаграммы.

2. Провести анализ чувствительности инвестиционного проекта.

3. Найти чистую приведенную стоимость (npv) и внутреннюю норму доходности (irr) проекта.

1. Анализ чувствительности денежных потоков инвестиционных проектов − это анализ того, как изменяются денежные потоки проекта при изменении одного или нескольких влияющих на них факторов.

Годовой денежный поток в условиях рассматриваемой модели равен бухгалтерской прибыли:

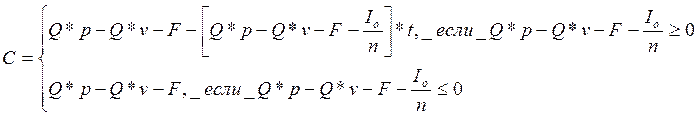          (1)

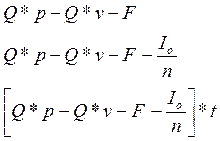где                                          − прибыль проекта до уплаты налога;

− бухгалтерская налогооблагаемая прибыль;

− налог.

Бухгалтерская налогооблагаемая прибыль:

П_но = 16000 * (13000 − 12100) − 4 млн. − 50 млн. / 4 = − 2,1 млн. < 0

Годовой денежный поток:

С =16000 * (13000 − 12100) − 4 млн.= 10,4 млн.

Если i− уровень инфляции, тогда цена единицы продукции в конце к-го года составит:

                                                    (2)

где  p_o− цена единицы продукции в начальный момент времени.

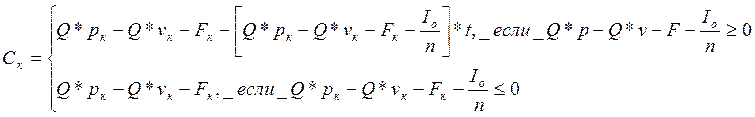(3)

Таблица 1

n	pk	vk	Fk	Р	Ck	С
0	−	−	−		−	-50000000
1	15600,00	14520,00	4800000	-20000	12480000	-37520000
2	18720,00	17424,00	5760000	2476000	14233200	-23286800
3	22464,00	20908,80	6912000	5471200	16329840	-6956960
4	26956,80	25090,56	8294400	9065440	18845808	11888848

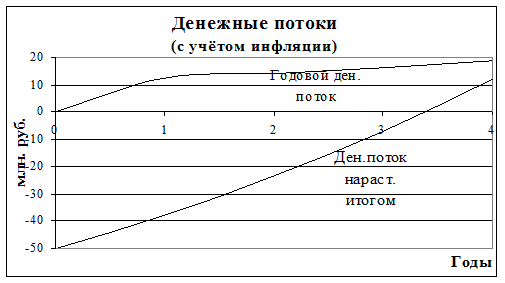
2. На практике невозможно абсолютно точно оценить будущие значения параметров, поэтому важно знать, как изменятся денежные потоки при отклонении параметров от своих ожидаемых значений. В случае, когда переменным параметром модели является количество выпускаемых в год единиц продукции, а остальные параметры являются постоянными величинами, формула примет вид арифметического выражения с одной переменной Q.

Значение ΔС можно получить с помощью частных производных:

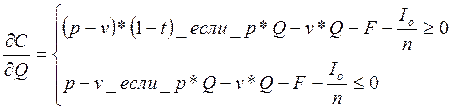                       (4)

jС/jQ = (13000 − 12100) = 900

Частная производная jС/jQ показывает, насколько денежных единиц изменится денежный поток при увеличении годового выпуска продукции на одну единицу. Поскольку денежный поток можно рассматривать как линейную функцию от объёма производства, из вышесказанного следует, что:

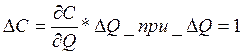                                      (4)

При изменении объёма производства на 60 шт. денежный поток изменится на сумму:

ΔС = 900 * 60 = 54000 руб.

          Таблица 2

Расчёт денежного потока

с учётом изменения объёма выпускаемой продукции, млн.руб.

Используя базовую формулу определения денежного потока, в случае необходимости можно найти производные от денежного потока по другим параметрам: jС/jp, jС/jv, jС/jF, jС/jI_o, jС/jt. Экономический смысл этих частных производных совпадает с экономическим смыслом производной jС/jQ, то есть частная производная от денежного потока по соответствующему фактору показывает, на сколько изменится денежный поток при изменении данного фактора на одну единицу.

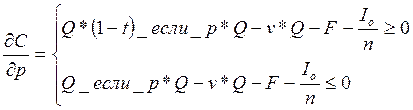                    (5)

jС/jр = 16000

При изменении цены выпускаемой продукции на 130 руб. денежный поток изменится на сумму:

ΔС = 16000 * 130 = 2080000 руб.

Таблица 3

Расчёт денежного потока

с учётом изменения цены выпускаемой продукции, млн.руб.

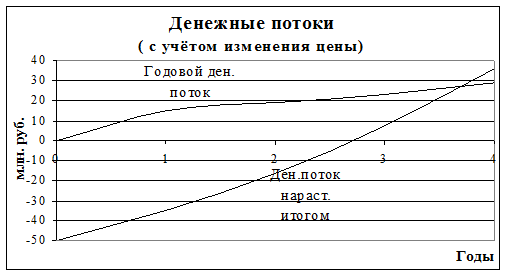
При реинвестировании проекта с коэффициентом реинвестирования (K_r ) в 32 %.

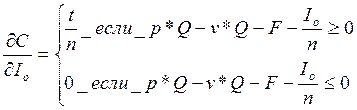                             (6)

jС/jI_o = 0

Таблица 4

Расчёт денежного потока

с учётом реинвестирования, млн.руб.

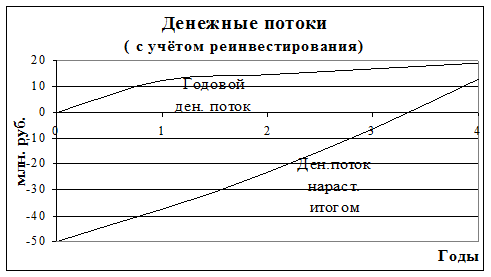
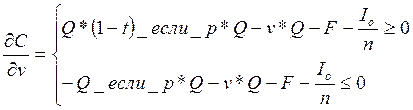                    (7)

jС/jv = −16000

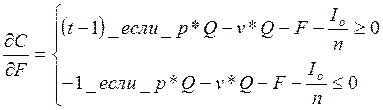                         (8)

jС/jF =  − 1

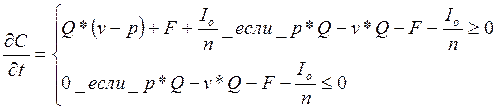      (9)

jС/jt = 0

При одновременном изменении нескольких параметров соответствующее изменение денежного потока определяется как:

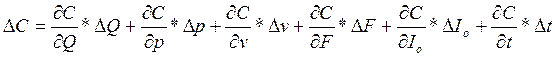      (10)

3. Корректировка реальной банковской процентной ставки с учётом инфляции производится по формуле:

                                                  (11)

l^’ = 0,12 + 0,2 + 0,12 * 0,2 = 0,344

4. Приведенная стоимость проекта pv(«present value»), показывающая, какую сумму необходимо вложить в альтернативный проект (в банк), чтобы через n лет капитализации получить сумму прибыли, равную прибыли данного проекта, определяется как:

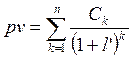                                               (12)

где  C_k − денежные потоки проекта по периодам;

n − срок проекта в периодах;

l’ − норма дисконтирования денежных потоков проекта с учётом инфляции.

Таблица 5

Расчёт приведенной стоимости проекта, млн.руб.

k	(1 + l’)k	Ck	Ck / (1 + l’)k
1	1,344	12,48	9,285714286
2	1,806	14,2332	7,879597151
3	2,428	16,32984	6,7264222
4	3,263	18,845808	5,775873691
∑			29,667607329

pv = 29667607,329 руб.

Таким образом мы видим, что для того чтобы получить через 6 лет капитализации сумму прибыли, равную прибыли нашего проекта, необходимо вложить в банк сумму в размере 29667607,329 руб.

Чистая приведенная стоимость проекта npv(«net present value») определяется как:

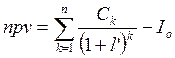                                        (13)

npv = pv − I₀ = 48739919,442 − 70000000 = − 21260081 руб.

Показатель npv показывает, что реализуемый нами инвестиционный проект требует инвестиционных вложений больше на сумму 20332392,67 руб., чем альтернативный проект, генерирующий аналогичные денежные потоки в будущем.

5. Внутренняя норма доходности проекта irr («internal rate of return») определяется нормой дисконтирования денежных потоков проекта, при которой чистая приведенная стоимость равна нулю:

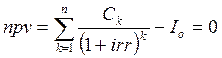                                          (14)

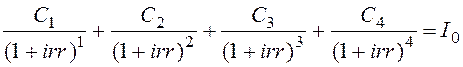
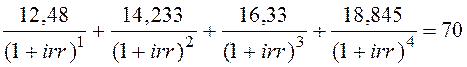
Использовав функцию ВСД (внутренняя ставка доходности для ряда потоков