конце контрольной работы указать, каким учебником или учебным пособием студент пользовался при изучении физики (название учебника, автор, год издания). Это делается для того, чтобы рецензент в случае необходимости мог указать, что следует студенту изучить для завершения контрольной работы.
Контрольная работа, признанная рецензентом удовлетворительной, хорошей или отличной оценивается словом «зачтено». Работа, признанная рецензентом неудовлетворительной оценивается словом «не зачтено». Если контрольная работа при рецензировании не зачтена, студент обязан представить её на повторную рецензию, включив в неё те задачи, решения которых оказались неверными. Повторную работу необходимо представить вместе с незачтённой. Если выполнен не свой вариант или не по действующим методическим указаниям, то она возвращается студенту без рецензирования. Студент должен быть готов дать пояснения по существу решения задач, входящих в контрольные работы. Если при собеседовании по контрольной работе установлено, что работа выполнена не самостоятельно, то работа не зачитывается.
Раздел 1.МЕХАНИКА
К И Н Е М А Т И К А
|
Поступательное движение |
Вращательное движение |
|
Средняя скорость
|
Средняя угловая скорость
|
|
Мгновенная скорость
В
проекции на ось C: |
Мгновенная угловая скорость
|
|
Пройденный путь
|
Угол поворота
|
|
Равномерное движение |
|
|
u = const S = ut |
w = const j = wt |
|
Неравномерное движение |
|
|
Ускорение
В проекции на ось C
|
Угловое ускорение
|
|
Равнопеременное движение |
|
|
a = const u =u0 ± at S = u0t ± at2/2 u2 - u02 = ± 2aS |
e = const w = w0 ± et j = w0t ± et2/2 w2 - w02 = ± 2ej |



![]()

![]() Криволинейное движение
Криволинейное движение
 |
|

|
|
|
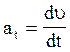 ,направлено по касательной.
Нормальное аn ускорение (характеризует изменение
скорости по направлению)
,направлено по касательной.
Нормальное аn ускорение (характеризует изменение
скорости по направлению)
|
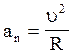 , -
, -
-направлено перпендикулярно вектору скорости
Полное ускорение:
![]() ;
;
![]()
Связь между линейными и угловыми величинами:
u = wR;
at = eR;
an = w2R;
w = 2pn = 2p/ T;
u = 2pnR = 2pR/ T.
|
Поступательное движение |
Вращательное движение |
|
Масса m |
Момент инерции I |
|
F |
Момент силы
где d - плечо силы |
|
Импульс (количество движения)
|
Момент импульса
|
|
Второй закон Ньютона
|
Основной закон динамики вращательного движения
|
|
Работа |
|
|
то A = Fs S = F S cos a |
то A = MDj |
|
Кинетическая энергия |
|
|
|
|
|
Законы сохранения (в замкнутой системе) |
|
|
Импульса
|
Момента импульса
|
Закон сохранения энергии:
Полная механическая энергия замкнутой системы остается постоянной, если между телами системы действуют только консервативные силы
Wк + Wп = const
Консервативные силы – силы, работа которых не зависит от формы траектории. К ним относятся силы тяжести, тяготения, упругости. Примером неконсервативных (диссипативных) сил являются силы сопротивления. Если в системе действуют не консервативные силы или система является не замкнутой, то есть действуют внешние силы, то энергия системы меняется на величину работы этих сил.
DW = A
Потенциальная энергия:
а) упруго деформированного тела
Wп = ![]()
где К- жесткость образца(пружины), X – абсолютная деформация б) тела, поднятого над землей
Wп= -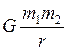
где G – гравитационная постоянная, m и m – массы тела(тела рассматриваются как материальные точки), r – расстояние между ними.
в) гравитационного взаимодействия
Wп = mgh
Силы, рассматриваемые в механике:
а) сила гравитационного взаимодействия
F =
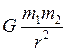
б) сила тяжести
P=mg
в) сила трения
Fтр= m× Fнд = mN
m- коэффициент трения, Fн.д- сила нормального давления, N - сила реакции опоры.
г) сила упругости (закон Гука): Fупр = -kx
Закон Гука можно записать в иной форме : s = Е×e
где s - напряжение, возникающее в образце.
s = ![]() ,
где S – площадь поперечного сечения образца.
Е – модуль Юнга.
,
где S – площадь поперечного сечения образца.
Е – модуль Юнга.
e = ![]() -
относительная деформация (относительное изменение)
-
относительная деформация (относительное изменение)
Уравнение
Бернулли 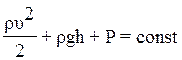
Примеры решения задач:
К И Н Е М А Т И К А
При решении задач по кинематике следует: определить характер движения тела; проанализировать, как меняются величины, характеризующие движение; записать уравнения, связывающие данные величины и те величины, которые надо найти при решении задачи.
Пример 1. Тело брошено вертикально вверх со скоростью 20 м/с. Найти максимальную высоту, на которую поднимается тело, и время движения. Сопротивление не учитывать.
|
uо = 20 м/с |
Движение тела - равнозамедленное -с ускорением свободного падения. |
|
|
hmax - ? t - ? |
g = 9,8 м/с2 » 10 м/с2 |
На максимальной высоте u = 0. Так как сопротивление отсутствует, то время движения вверх и вниз одинаково
t= t¯ = t/2.
Для движения имеют место уравнения: u = uо - gt (1)
u2 - uо 2 = -2gh (2
Если t = 2t, то u = 0, тогда 0 = u0 - gt.
Откуда t = uо/g, всё время движения: t = 2t = 2 uо/g (3)
Если h = hmax, то u = 0, и из уравнения (2) имеем u02=2ghmax,
откуда hmax = uо2/2g (4)
Размерность (3) и (4): [t] = м×c2/c×м = c; [h] = м2с2/c2м = м;
Вычисления: t = 2×20/10 = 4 c, hmax = 400/2×10 = 20 м.
Ответ: t = 4c, hmax = 20 м.
Пример 2. Тело брошено под углом 60о к горизонту со скоростью 20 м/с. Найти дальность полета по горизонтали, максимальную высоту подъёма и радиус кривизны траектории через 1с после начала движения. Сопротивление не учитывать.
|
uо = 20 м/с a = 600 t1 = 1 c |
||
|
Hmax - ? S - ? R - ? |
Разложим вектор начальной скорости на две составляющие - горизонтальную ux= u0cosa и вертикальную uoy = u0sina. Движение по криволинейной траектории можно рассматривать как сложное, состоящее из двух движений: по горизонтали - с постоянной скоростью (т.к. в этом направлении силы не действуют) ux = const, тогда
S = uxt, (1)
а по вертикали - равнопеременное движение с ускорением свободного падения g. Уравнения для этого движения:
uy = uoy - gt (2)
h = uoy t - gt2/2 (3)
uy2 - uoy2 = -2gh (4)
Так как в верхней точке траектории uy = 0, тогда из уравнения (4) имеем
uoy2 = 2gHmax .
Откуда Hmax = uoy2 / 2g = uo2sin2a/2g (5)
Из уравнения (2) найдём время подъёма тела на максимальную высоту, учитывая, что в верхней точкеuy = 0
u = u0y - gt.
Откуда t = uoy/g = uosina/g.
Всё время движения t = t + t¯ = 2t, t = 2uosina / g. (6)
Подставляя в уравнение (1), найдём дальность полёта тела по горизонтали
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.