Основные понятия и определения электроники. Компонентная база электроники, страница 15

                                         U_вых(t) = -R C  ^d (U_вх(t)).                      (4.8)

dt

Таким образом, данная схема дифференцирует в реальном времени входной сигнал. Например, при подаче на вход линейно нарастающего напряжения на выходе появится постоянное напряжение, поскольку производная от линейной функции – это константа.

Интегратор и дифференциатор могут использоваться в АВМ для решения, соответственно, интегральных и дифференциальных уравнений. Кроме того, интегратор применяется в устройствах формирования выдержки времени и в аналого-цифровых преобразователях.

4.5. Частотные фильтры

Частотные фильтры на ОУ – это усилители с коэффициентом усиления, зависящим от частоты. Бывают фильтры низких частот (ФНЧ), фильтры высоких частот (ФВЧ) и полосовые фильтры (ПЧФ).

Схема инвертирующего фильтра низких частот на основе интегратора и его амплитудо-частотная характеристика (АЧХ) приведены на рис. 4.8.

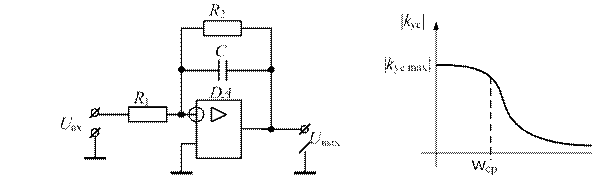
Рис. 4.8. Схема инвертирующего фильтра низких частот и его амплитудо-частотная характеристика

Фильтр низких частот имеет значение коэффициента усиления, близкое к его максимальному значению k_{ус max} при низких частотах входного напряжения. При постоянном входном напряжении, когда w= 0, сопротивление конденсатора C стремится к бесконечности и фильтр превращается в инвертирующий усилитель с коэффициентом усиления, равным

                                                                   kус = kус max = - R2 .                            (4.9)

R₁

При высоких частотах сопротивление конденсатора C стремится к нулю, и коэффициент усиления также стремится к нулю. Таким образом, фильтр подавляет высокие частоты и усиливает низкие частоты.

Частоту, при которой АЧХ фильтра начинает резко изменяться, называют частотой среза w_ср. Для рассматриваемой схемы она равна

                                                     w_ср = ¹ .                                 (4.10)

R₂ C

При расчете параметров фильтра задаются требуемыми значениями kус max и wср.

Фильтр высоких частот можно реализовать на основе дифференциатора (рис. 4.7) или других схем. 

Вариант схемы фильтра высоких частот и его АЧХ приведен на рис. 4.9.

                                           R3

|kус|

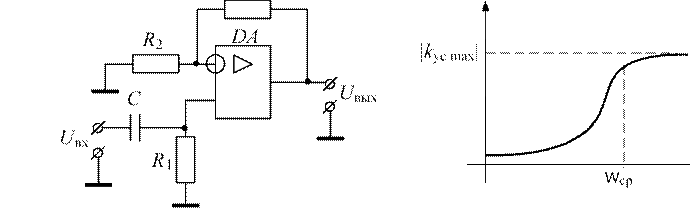
Рис. 4.9. Схема фильтра высоких частот и его амплитудо-частотная характеристика

Фильтр высоких частот имеет значение коэффициента усиления, близкое к его максимальному значению k_{ус max} при высоких частотах входного напряжения. При wfi¥ сопротивление конденсатора C стремится к нулю, и фильтр превращается в неинвертирующий усилитель с коэффициентом усиления, равным R

R₁ C

Более высокой крутизной АХЧ на переходной полосе частот обладают частотные фильтры второго порядка, содержащие два последовательно соединенных фильтра первого порядка.

Фильтры высоких и низких частот применяются в измерительных устройствах для исключения влияния части гармонических составляющих измеряемого сигнала на результат измерения.

Схема инвертирующего полосового фильтра (избирательного усилителя) на основе двойного Т-образного моста и его АЧХ приведены на рис. 4.10.

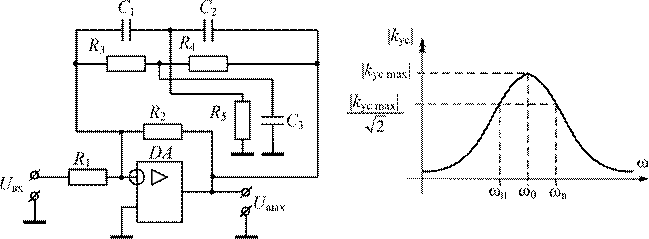
Рис. 4.10. Схема инвертирующего полосового фильтра на основе двойного Т-образного моста и его АЧХ

Двойной Т-мост собран на резисторах R₃, R₄ , R₅, конденсаторах C₁, C₂, C₃ и включен в обратную связь инвертирующего усилителя, собранного на ОУ DA и резисторах R₁ , R₂ . На частоте квазирезонанса w₀ фильтр имеет максимальный коэффициент усиления, а на остальных частотах коэффициент усиления снижается. При условии, что

R₃ = R₄ = 2 R₅ = R и C₁ = C₂ = ^C3 = C , частота квазирезонанса равна 2

                                                      w₀ ^{= 1}                                                            .    (4.13)