Критерии и методы проверки датчиков случайных чисел

Критерии и методы проверки датчиков случайных чисел

Хотя это и важно, но большой период еще вовсе не означает, что последовательность хороша для работы. Далее будем рассматривать статистические тесты для проверки генераторов случайных чисел, когда ЭВМ манипулирует с группами чисел последовательности и производит оценку с помощью определенных статистических критериев.

Универсальные тесты для анализа случайных последовательностей

Критерий χ2. Предположим, что все возможные результаты испытаний разделены на k категорий. Проводится n независимых испытаний (исход каждого испытания не влияет на исход остальных). Пусть p_s - вероятность того, что результат испытания попадет в категорию s, и пусть Y_s  – число испытаний, которые действительно попали в категорию s. Сформируем статистику:

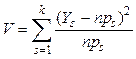                                  (3)

Формулу (3) можно преобразовать к виду, более удобному для  вычислений:

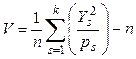                                  (4)

Затем V сравнивается с числом из таблицы для распределения c² при количестве степеней свободы n=k–1. Если V меньше значения, соответствующего p=0.99, или больше значения, соответствующего p=0.01, то результаты бракуются как недостаточно случайные. Если p лежит между 0.99 и 0.95 или между 0.05 и 0.01, то результаты считаются "подозрительными". При значениях p, заключенных между 0.95 и 0.90 или 0.10 и 0.05, результаты "слегка  подозрительны". Часто с помощью критерия c² проверяют по крайней мере три разные части исследуемого ряда чисел. Если не менее двух раз из трех результаты оказываются подозрительными, числа  отбрасываются как недостаточно случайные.

Возникает вопрос о длине n последовательности случайных чисел, которую необходимо выбрать для данного теста. Теоретические расчеты показывают, что достоверные оценки получаются в том случае, когда в каждую из категорий попали не менее 5 испытаний, т.е. выполняется условие Y_s > 4, s=1..k.

Критерий Колмогорова–Смирнова (КС–критерий). Критерий c² применяется в тех случаях, когда результаты испытаний разделяются на конечное число k категорий. Однако часто случайные величины могут принимать бесконечно много значений. В теории вероятностей и математической статистике непрерывные случайные величины описываются с помощью функции распределения:

F(x)=p{X£x}                                     (5)

Используя значения x₁, x₂, ..., x_n случайной величины X, можно построить эмпирическую функцию распределения

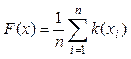,                                  (6)

где .

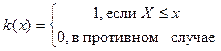При увеличении n функции F_n(x) должны все более точно аппроксимировать F(x). КС-критерий можно использовать в тех случаях, когда F(x) не имеет скачков, и он должен указать, насколько маловероятны большие расхождения между F_n(x) и F(x). Для этого используются следующие статистики:

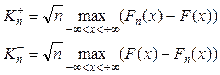                           (7)

K_n⁺ показывает, каково максимальное отклонение для случая F_n>F, а K_n^-  для F_n<F. Множитель  нормирует статистики (7) таким образом, чтобы стандартное отклонение не зависело от n. Далее, как и в случае критерия c², сравнивают значения (7) с табличными и определяют, имеют ли они высокую или низкую значимость.

Формулы (7) не годятся для машинных расчетов, так как требуется отыскать максимальное среди бесконечного множества чисел. Однако, учитывая, что F(x) неубывающая функция, а F_n(x) имеет конечное число скачков, можно определить статистики (7) с помощью следующего алгоритма.

1.  Определяются выборочные значения x₁, x₂, ... , x_n.

2.  Значения x_i  располагаются в порядке возрастания так, чтобы x₁£x₂£...£x_n.

3.  Статистики (7) вычисляются по следующим формулам:

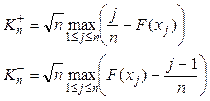                            (8)

KС-критерием можно пользоваться в сочетании с критерием c², чтобы получить лучшую процедуру отбраковки датчиков, чем правило «два подозрительных из трех проверок». Пусть с помощью критерия c² были независимо обработаны 20 разных участков случайной последовательности, в результате чего были получены значения V₁, V₂, ..., V₂₀. По этим значениям строится эмпирическая функция F₂₀(x) и сравнивается с теоретической функцией распределения, которую можно получить из таблиц распределения c². После определения статистик K₂₀⁺ и K₂₀^- формируется окончательное суждение об исходе проверки последовательности с помощью КС-критерия. В результате часто удается выявить как локальные, так и глобальные отклонения от заданного закона распределения.

Специализированные тесты

В этом пункте будут описаны специализированные тесты, которые могут быть использованы исключительно для проверки качества датчиков базовых случайных чисел. Каждый тест применяется к последовательности случайных чисел