Классификая математических моделей. Моделирование случайных воздействий, страница 2

Такие программные методы называются датчиками (генераторами) псевдослучайных чисел.

	-	+
1	Большой объем Изменяемость	просто
2	Уникальность чисел Размеры Потребление энергии	Уникальность чисел
3	Качество чисел	Стоимость Скорость

Будем рассматривать следующие последовательности псевдослучайных чисел:

х₁, х₂…           0 ≤ х_i  < m

u₁, u₂…           0 ≤ u_i  < 1        u_i = x_i / m       

y₁, y₂ …          0 ≤ y_i  < d        y_i = (х_i * d) div m

Достаточные для многих практических задач генераторы случайных чисел представляют собой частные случаи следующей схемы:

x_n+1 = (a*x_n + с) mod m         , n³0    - линейная конгруэнтная последовательность

x₀ – начальное значение

m – модуль

a – множитель 0 < a < m

с – приращение 0 ≤ c < m    с=0 мультипликативный метод, с ≠0 смешанный метод

Любая линейная конгруэнтная последовательность всегда зацикливается, т.е. числа образуют цикл, который повторяется бесконечное число раз. Повторяющийся цикл называется периодом.

x_n+1=(3x_n+1) mod 13

2,7,9,2,7,9,2… период

1,4,0,1,4,0…

5,3,10,5,3,10…

6,6,6,6,6,6…

Алгоритм получается эффективным при выборе m, равным размеру машинного слова (разрядности используемого типа).

Такой выбор имеет недостаток: младшие цифры числа х намного менее случайны, чем старшие. Подобной ситуации не возникает, когда m является простым числом. Для увеличения длины периода логично выбрать m наибольшим простым числом для используемого типа данных. Как компромисс можно рассматривать вариант m= 2^k -1 (k – разрядность), в этом случае mod m можно вычислить упрощенным способом.

Для получения периода максимальной длины m, множитель а и приращение с должны удовлетворять определенным условиям.

При с=0 и m=2^k максимальный период = 2^k-2 и он достигается при:

1) a mod 8 =3

2) a mod 8 =5

Рассмотренные последовательности не единственные. Хорошие результаты могут быть получены с помощью квадратичного конгруэнтного метода.

x_n+1=(аx_n²+bx_n+c)mod m

Для получения датчика с периодом, большим m, для генерации очередного числа можно использовать несколько предыдущих, а не одно. Простейшим и чрезвычайно эффективным по скорости способом является аддитивный датчик, основанный на преобразовании вида:

x_n=(x_n-1+x_n-2+…+x_n-k)mod m

x_n=(x_n-1+x_n-2+…+x_n-k)mod 10

1,2,3,6,1,0,7,8,5,0,3,8,1,2,1,

4,7,2,3,2,7,2,1,3,4,7,4,5,6,

5,6,7,8,1,6,5,2,3,0,5,8,3,6,7

Существует класс методов, комбинирующих несколько датчиков для получения «еще более случайных» последовательностей.

Две псевдослучайные последовательности X_n и Y_n (0≤ y_n < k)

0    1    2                     k-1

…

V  

1. y_i

2. V[y_i] – случайное число

3. V[y_k] =X_n

 

Если периоды последовательностей <X_n> и <Y_n> взаимно простые, то период датчика невероятно большой.

КРИТЕРИИ И МЕТОДЫ ПРОВЕРКИ ДАТЧИКОВ СЛУЧАЙНЫХ ЧИСЕЛ

Хотя большой период и важен, но он не гарантирует, что последовательность хороша для работы. Существуют различные тесты, позволяющие оценить качество последовательности.

1. Универсальные тесты.

Критерийχ²

С помощью этого критерия проверяется равномерность распределения случайных чисел по всему диапазону их возможных значений.

Критерий:

- результаты испытаний разделены на k категорий

- проводится n независимых испытаний

- пусть p_s – теоретическая вероятность того, что результат испытания попадет в категорию s ( s=[1, k] )

- пусть Y_s  – число испытаний, которые действительно попали в категорию s

Вычисляется: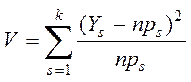

Значение V сравнивается с табличным значением.

ХИ2ОБР (уровень значимости = α; степени свободы = k-1) – хитрая формула из экселя

При проверке на равномерность табличное значение для соответствующих уровней значимости располагают на отрезке (координатной прямой).

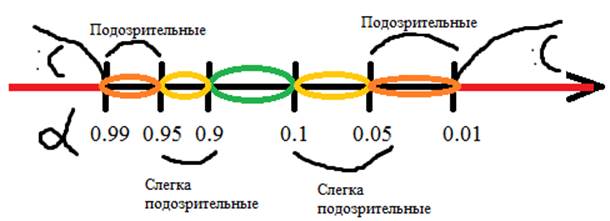
Анализируется, в какой отрезок попало значение V. Если попало в самые крайние значения, то результаты бракуются как недостаточно случайные.

Проводится не менее 3 проверок. Если не менее 2 раз из 3 результаты оказываются подозрительными, то числа отбрасываются как недостаточно случайные.

Для применения критерия χ² требуется, чтобы в каждую категорию попало не менее 5 испытаний.