Классификая математических моделей. Моделирование случайных воздействий

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

ТЕОРИТИЧЕСКИЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Моделью объекта называется всякий предмет (или символы), отражающие определенные характеристики моделируемого объекта.

Под моделированием понимаем исследование различных объектов с помощью модели. Мат. Моделью наз. Определенную совокупность мат. символов (алгоритмов), действие над которыми моделируют (воспроизводят) определенные характеристики моделируемого объекта или явления

Информация – свойства объекта, отражающиеся во внешний мир и которые могут быть восприняты другим объектом.

Под системой понимаем совокупность людей и объектов (машин, механизмов, процессов), объединенных для достижения определенных целей.

Характерные особенности систем:

1. Наличие цели и функционирования. Эти цели достигаются выполнением ряда задач, стоящие перед элементами и подсистемами.

2. Возможность управления, сущность которого состоит в том, чтобы в процессе функционирования были достигнуты цели.

3. Иерархическое построение (система-подсистема-элементы)

Простейшая схема любой системы может быть представлена в виде 2 подсистем:

- подсистема управления;

- подсистема, реализующая основное целевое назначение.

Процесс управления системой начинается со сбора первичной информации. В результате анализа и оценки обстановки вырабатываются различные альтернативные варианты решения.

Если решения могут быть физически осуществлены при функционировании системы, то они называются допустимыми.

Решения называются рациональными, если они соответствуют целям функционирования системы.

Решения называются оптимальными, если они соответствуют целям функционирования системы, но при этом показатель эффективности системы (некоторая количественная мера) достигает своего экстремального значения.

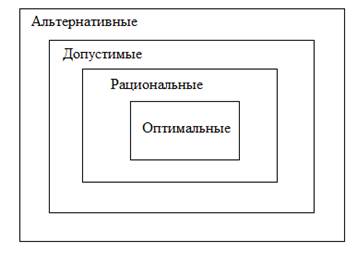
Из множества вариантов решений принимается только одно, которое передается в управляемый орган.

Процедура принятия решения разделяет системы управления на:

- автоматические

- автоматизированные

В автоматической системе алгоритм принятия решения заранее сформулирован человеком для всех возможных ситуаций и заложен в какое-то техническое устройство.

В автоматизированной системе решение принимается с участием человека и технические средств.

Помимо математического также используется и физическое (аналоговое) моделирование – состоит в изучении системы по средствам анализа некоторого макета, сохраняющего физическую природу системы.

КЛАССИФИКАЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

В зависимости от соотношений связывающих состояния и параметры выделяют следующие модели:

1. Детерминированные. Состояние системы однозначно определяется через ее параметры, входную информацию и начальные условия.

2. Стохастические. По распределениям вероятности для начальных условий параметров и входной информации определяется распределения вероятностей для состояний систем.

По характеру изменения внутренних процессов выделяют:

1. Непрерывные. Состояние системы меняется в каждый момент времени моделирования.

2. Дискретные – система переходит из одного состояния в другое в фиксированный момент времени. А на непустых интервалах  между ними состояние не меняется.

По возможности изменения свойств во времени:

1. Динамические – свойства меняются

2. Статические – не меняются

МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЙ

На функционирование реальных сложных систем оказывают влияние случайные факторы. Примерами таких случайных факторов являются случайные промежутки времени между поступлениями запросов на сетевой сервер, деталей на производственный участок, вызовов в АТС, временные интервалы обработки запросов и деталей, установления связи и длительности разговоров и т.д.

Поэтому при построении моделей сложных систем возникает необходимость в имитации случайных факторов по заданным законам распределения вероятностей.

Случайные воздействия, заменяющие отброшенные при построении модели элементы описания системы, могут быть получены следующим образом:

1  - вводиться в модель в виде таблиц экспериментальных результатов, полученных в процессе натурных испытаний замененных элементов;

- искусственно воспроизводиться программными датчиками:

2. аппаратные датчики случайных чисел

3. программные датчики случайных чисел

Возникает вопрос как может быть случайной последовательность, выработанная по детерминированному алгоритму. Ответ заключается в том, что достаточно, чтобы эта последовательность выглядела как случайная, т.е. обладала свойствами случайной последовательности.