Раскраска графов. Свойства хроматического числа. Примеры задач, которые сводятся к нахождению хроматического числа

Контрольная работа № 1

по мат. моделям

Номер варианта смотри в «список_2курс.xls»

Задание №1 Раскраска графов

Теоретические сведения.

Определение. Пусть G=(V,E) – обыкновенный граф и k – натуральное число. Функция f: V→{1,…,k} называется раскраской графа. Раскраска называется правильной, если для любых смежных вершин x,y Є V справедливо неравенство f(x) ≠ f(y). Число k – число красок раскраски f.

Как правило, будем представлять себе, что мы раскрашиваем вершины некоторым набором красок (в количестве k штук). Правильность раскраски означает, что смежные вершины раскрашиваются в разные цвета.

Определение. Наименьшее число красок, необходимое для правильной раскраски графа G называется хроматическим числом графа G. Правильную раскраску таким числом красок будем называть оптимальной.

Рассмотрим примеры графов, изображенных на рисунке.

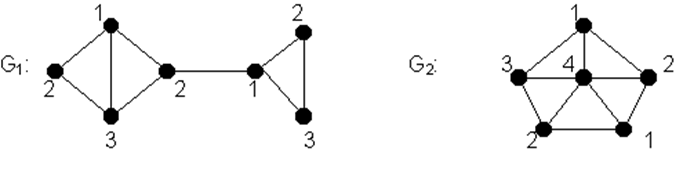
Рисунок 1 – Примеры графов с раскраской

Оба графа содержат трехэлементный полный подграф К3, поэтому для правильной раскраски необходимо, по крайней мере, три краски. Для графа G1 этого достаточно (см. рисунок). Граф G2 имеет цикл длины 5. Нетрудно понять, что для правильной раскраски вершин цикла необходимо три краски. Но центральная вершина графа G2 смежна со всеми вершинами цикла, поэтому для правильной раскраски графа понадобится четвертая краска (см. рисунок). Итак, c (G1)=3 и c (G2)=4.

Свойства хроматического числа:

1.  Граф G является 2-хроматическим тогда и только тогда, когда он не содержит циклов нечетной длины.

2.  Аналогичными свойствами обладает двудольные графы. Отсюда следует, что 2-хроматический граф – 2-дольный граф. Также любое дерево является двудольным графом.

3.  Если максимальная степень вершин простой граф G есть S(G), то .

4.  Граф G с максимальной степенью в S(G) является S-раскрашенным, за исключением двух случаев:

Ø при S(G)>2 граф не является циклом некоторой длины;

Ø при S(G)>2 граф G не является полным графом.

5.  Данная оценка является хорошей, если степени всех вершин имеют