



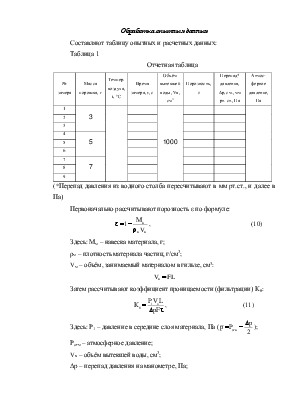

Цель работы – определение удельной поверхности сыпучих материалов и катализаторов по сопротивлению фильтрации воздуха через слой (Метод Б.В. Дерягина).
Для многих технологических процессов удельная поверхность как характеристика дисперсности удобна тем, что выражается только одной величиной. Зная удельную поверхность Sуд, можно определить средний диаметр частиц dср из зависимости:
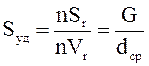 , (1)
, (1)
где: n – число частиц в пробе;
Sr и Vr – внешняя поверхность и объем частицы диаметром dср, причем
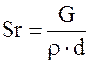 ,
(2)
,
(2)
здесь: G – масса пробы или навески; ρ – плотность материала частиц.
Удельную поверхность частиц измеряют различными методами. Наибольшей простотой отличается фильтрационный метод или метод определения Sуд воздухопроницанием при давлении близком к атмосферному (применим для частиц с d ≤ м мм). Метод основан на закономерностях ламинарного движения воздуха через слой сыпучего материала.
Гидравлическое сопротивление Δp (Па) слоя сыпучего материала высотой L (м) при ламинарном движении потока газа или жидкости можно рассчитать по формуле:
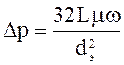 ,
(3)
,
(3)
где: μ и ω – динамический коэффициент вязкости (Па·с) и скорость потока (м/с) соответственно;
dэ – эквивалент диаметр межзерновых каналов, причем:
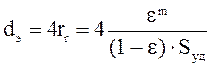 ,
(4)
,
(4)
Здесь:
rr – гидравлический радиус,
ε – порозность,
m=1,25 – коэффициент, учитывающий застойные зоны.
Слой сыпучего материала может уплотняться в различной степени, причем значение Sуд будет оставаться неизменным. При этом предполагается, что движение воздуха через слой материала аналогично его движению через капилляры переменного сечения и различной извилистости.
Внутренняя поверхность капилляров в единице объема слоя равна удельной поверхности измельченного материала.
Суммарное поперечное сечение капилляров соответствует порозности ε, то есть доле объема, не занятого дисперсным материалом. Длину капилляров принимают близкой к высоте слоя порошка. Скорость течения воздуха определяют с учетом застойных зон.
Закон Пуазейля для процессов фильтрации газа или жидкости через слой сыпучего материала принимает вид:
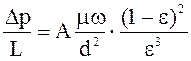 ,
(5)
,
(5)
где: А – коэффициент пропорциональности.
С учетом этого закона выражение для удельной поверхности Sуд (м2/м3) можно записать
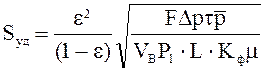 ,
(6)
,
(6)
где: F – площадь поперечного сечения слоя, м2;
τ – продолжительность фильтрации воздуха, с;
![]() -
среднее давление в слое дисперсного материала, равное
-
среднее давление в слое дисперсного материала, равное
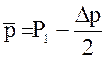 ,
(7)
,
(7)
Р1 – давление воздуха перед слоем дисперсного материала, Па;
Vв – объём профильтрованного воздуха в условиях вязкого потока, м3;
Кф – коэффициент формы капилляра, по опытным данным равный 2,5.
При движении воздуха через слой высокодисперсного материала с размером частиц < 100 мкм наблюдается отклонение от закона Пуазейля, вызванные появлением эффекта "скольжения" воздуха относительно зерен слоя. С уменьшением размера зерен доля потока скольжения обычно возрастает и может составлять до 80: всего потока воздуха. С учетом потока "скольжения" уравнение (7) примет следующий вид:
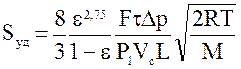 ,
(8)
,
(8)
где: Vc – объём потока, обусловленный скольжением газа, см3;
R – газовая постоянная (8,315 эрг/К.моль);
Т – абсолютная температура, К;
М – мольная масса воздуха, кг/моль.
О появлении в фильтрационном потоке "скольжения" можно судить по значению коэффициента П1, учитывающего структуру слоя, а также физические свойства потока
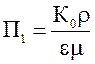 ,
(9)
,
(9)
где: К0 – общий коэффициент
фильтрации газа (или проницаемости слоя), равный 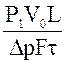 ,
,
V0 – общий объём профильтрованного газа, м3;
ρ – плотность воздуха, кг/м3;
μ – динамический коэффициент вязкости газа, Па·с.
В переделах изменения безразмерного коэффициента П1 от 100 до 0,1 в потоке газа наблюдают как вязкое течение, так и скольжение, в области П1 > 100 только вязкое течение газа.
Описание установки.
На дно гильзы помещают кружок фильтровальной бумаги и заполняют её 3 г исследуемого порошка. Затем подготавливают измерительную часть установки. Для этого открывают кран между термостатом и сосудом Мариотта
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.