Параболическая зеркальная антенна. Принцип действия зеркальной антенны. Облучатели зеркальных антенн. Расчет параметров антенны

Оглавление

1.             Теоретические сведения. 3

1.1.          Параболическая зеркальная антенна. 3

1.2.          Принцип действия зеркальной антенны. 4

1.3.          Облучатели зеркальных антенн. 6

2.             Практическая часть. 7

2.1.          Исходные данные. 7

2.2.          Расчет параметров антенны.. 7

2.3.          Расчет профиля зеркала. 9

2.4.          Расчет облучателя. 10

2.5.          Расчет амплитудного распределения по раскрыву зеркала. 13

2.6.          Расчет ДН зеркальной антенны.. 15

2.7.          Расчет допуска на точность изготовления. 19

Заключение. 20

Список используемой литературы.. 21

Теоретические сведения.

1.1. Параболическая зеркальная антенна.

Параболическая антенна (рис. 1,а) или антенна с параболическим зеркалом — одна из наиболее часто применяемых в радиолокации антенн. При равномерном облучении зеркала ДН параболической антенны является иглообразной. При облучении только части зеркала можно получить плоскую ДН. Параболические зеркальные антенны используются в РЛС для поиска и сопровождения целей, для решения большинства задач радиолокации.

Геометрические соотношения. Предполагается, что поверхность зеркала является идеально проводящей. В фокусе F зеркала расположен точечный облучатель. Из геометрических соотношений следует, что сферическая волна исходящая из фокуса F и попадающая на зеркало, преобразуется после отражения в плоскую волну, распространяющуюся в направлении положительной оси параболоида (рис. 1, б).

Уравнение поверхности параболоида имеет вид

         (1)

где f= OF- фокусное расстояние параболоида (начало координат системы в точке О).

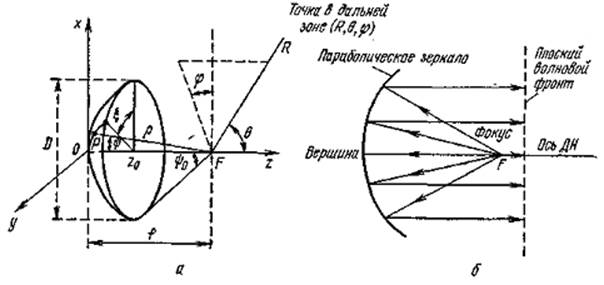
Рис. 1 Геометрические соотношения в антенне с параболическим зеркалом (а), принцип работы параболической антенны(б).

Угловой размер апертуры и диаметр зеркала D связаны следующей формулой:

       (3)

Угловой размер апертуры  показан на рис. 2 как функция f/D. Проектирование зеркала состоит в выборе параметров f/D  и 2:

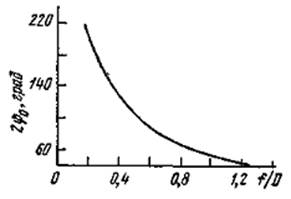
Рис.2. Зависимость полного углового размера апертуры 2от f/D  для параболического зеркала.

распределения тока может объяснить зависимость уровня боковых лепестков от параметра KНД.

Требуемый КНД антенны определяет выбор диаметра апертуры D. Если задан КНД G_D, то

         (4)

1.2.  Принцип действия зеркальной антенны.

Зеркальная антенна представляет собой систему, состоящую из облучателя (слабонаправленной антенны) и металлического отражателя (зеркала). Форма зеркала определяется требованиями к диаграмме направленности антенны и может быть различной. В простейшем случае, когда диаграмма направленности не должна быть слишком узкой и не требуется какой-либо специальной формы ее, отражатель может быть плоским. Для получения диаграммы направленности с осевой симметрией применяют отражатель в форме параболоида вращения. Диаграммы направленности с различной шириной в вертикальной и горизонтальной плоскостях получают с помощью отражателей в виде усеченного параболоида или параболического цилиндра.

Рассмотрим принцип действия антенны с отражателем в виде параболоида вращения. Параболоид вращения представляет собой поверхность, описываемую параболой при вращении ее вокруг оси. Сама же парабола является геометрическим местом точек, равноудаленных от точки F, называемой фокусом, и прямой, называемой директрисой (рис. 3). Расстояние от фокуса до параболы вдоль фокальной оси называется фокусным расстоянием f, а расстояние от фокуса до директрисы — параметром параболы p = 2f. В декартовой системе координат с началом в вершине параболы уравнение параболоида вращения имеет вид

                                    (1)

Парабола обладает тем важным свойством, что нормаль к ней в каждой точке (например, в точке A₁) делит

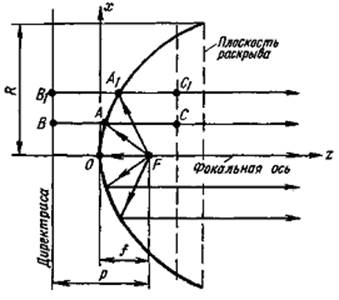
Рис.3. Параболическая антенна

пополам угол между направлением на фокус и направлением, параллельным фокальной оси. Если точечный облучатель, излучающий сферическую электромагнитную волну, т. е. волну, у которой фазовый фронт — сфера, поместить в фокус, то в соответствии с этим свойством облучающая волна будет отражаться от всех точек параболоида в параллельных его оси направлениях. При этом расстояния, проходимые волной от фокуса до любой точки на параболоиде и от нее до любой плоскости, перпендикулярной его оси, одинаковы. Действительно, поскольку по определению параболы AF=AB, A₁F=A₁B₁, ... , то FA+AC=BA+AC=B₁A_l+A₁C₁=FA₁+ A₁C₁= . . ., вследствие этого во всех точках плоскости, перпендикулярной оси параболоида, фаза поля отраженной волны одинакова.

Волна, фазовый фронт которой плоскость, называется плоской, Таким образом, параболический отражатель преобразует сферическую волну облучателя в плоскую волну, распространяющуюся только в одном направлении.

Однако волна остается плоской только в пределах отражателя. Пройдя плоскость раскрыва отражателя, она вновь начинает расходиться в стороны, и на расстояниях, значительно превосходящих диаметр раскрыва, фронт ее снова становится сферическим. Направленность излучения при этом существенно зависит от отношения радиуса раскрыва R к длине волны λ. Чем больше это отношение, тем больше направленность, т.е. тем меньше расходится волна в стороны от фокальной оси.

Заметим, что облучатели радиолокационных антенн имеют размеры, сравнимые с длиной волны или даже превосходящие ее. Поэтому с фокусом параболоида должен совмещаться так называемый фазовый центр облучателя, под которым понимают центр излучаемой им сферической волны. Фазовый центр обычно определяют экспериментально.

1.3. Облучатели зеркальных антенн.