Особенности расчета поля в дальней зоне антенны. Максимальный линейный размер излучающей системы. Смысл множителя системы

Поскольку при всех значениях р „ имеем ри < г, то можно разложить кп, описываемое (1.1 б) в ряд по степеням отношения p„/r:

           rn=r 1—      COS                   (1.17)

В дальней зоне излучающей системы можно ограничиться первыми двумя членами ряда, т.е. положить cosan.           (1.18)

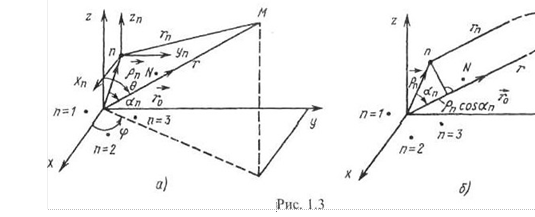
Указанное равенство равносильно тому, что лучи, проведенные в точку наблюдения М из начала общей системы координат и из точки расположения излучаемого элемента, считаются параллельными (см. рис. 1.3, б). Величина p„cosa = дг носит название разности хода лучей. Из параллельности лучей сразу следует равенство угловых координат: О = 0, = (Р. Следовательно, векторы Е , создаваемые отдельными излучателями в точке наблюдения, параллельны между собой; компоненты результирующего вектора можно находить как сумму ком-

понент каждого из элементарных полей; для каждой из компонент поля можно вынести из-под знака суммы функцию, соответствующую комплексной ДН.

Что касается величины l/r , влияющей на амплитуду поля (1.15), то ее можно заменить на 1/r. Возникающая при этом погрешность (оценим ее по модулю, поскольку rn может быть как больше, так и меньше к)

1

(1.19)

где D — максимальный линейный размер излучающей системы. При больших значениях r погрешность б «

Естественно, что принятые выше допущения тем строже, чем больше расстояние r. Определим более точно, при каком расстоянии можно ими пользоваться. Основная погрешность при замене (1 .17) соотношением (1.18) определяется третьим слагаемым в квадратных скобках (1, 17). Отбрасывание этого слагаемого дает ошибку при вы-

 2

числении фазового множителя, равную k —Lsin² . При максимальном значении sina = 1 (а = п/2) и рп =D/2 (при расположении начала общей системы координат в середине излучающей системы) эта ошибка равна 0²/4ir. Если потребовать, чтобы фазовая ошибка не превышала п/8, т.е. 22,5 ⁰ , то необходимо, чтобы

          2D2/i.                                                                           (1.20)

Из (1.20) следует, что с увеличением размеров излучающей системы граница дальней зоны резко отодвигается от антенны. Так, если D = ОХ, то дальняя зона начинается с = 2001. При частоте 10 ГГц (Х = З см) это расстояние составит 6 м. При D = 1001. граница дальней зоны начинается с расстояния к = 20000i, что соответствует 600 м.

Отметим еще раз, что условие (1.20) дает верхнюю границу дальней зоны во всем секторе углового положения точек наблюдения относительно антенны, поскольку оно справедливо для углов ан, близких к п/2. При значениях (Мп, близких к нулю, требования к расстоянию г, при которых справедлива замена (1.17) на (1.18), значительно ослабляются, т.е. граница дальней зоны в этих направлениях приближается

к антенне и определяется, по существу, уже не фазовыми ошибками при суммировании (l.l4), а амплитудными погрешностями, обусловленными отличием r r. Таким образом, при заданной геомари_и антенны граница дальней зоны зависит углового положения точек наблюдения.

Обычно расстояние между передающей антенной и точкой приема существенно большс, чем это требуется формулой (1 .20), однако знание границы дальней зоны важно при экспериментальном Исмедовании характеристик антенн, в частности при измерении ДН.

Вернемся к процсдурс нахождения результирующего поля, излучаемот системой из дискретных излучателей с ИЗВ"СТНЫМ законом распределения тока в элементах. В дальней зоне выражение для поля п-го излучателя ( 1 . 1 5) в единой системе координат r, е, ф примет вид

          lnfo (Э, ф)          kr)exp(i Кря cos ал).

В общем виде разность хода дл = р, cosu, может быть вычислена как проекция вектора рп = .ioxn + упуп + zoz„ , где х , у — координаты точки расположения п-т излучателя, на орт r о, который, используя формулы псрехоца от декартовых координат к сферическим [14], можно представить в виде

         = .io sin ecosp-€ уо sin esinq)+ cos9.                            (122)

Соответственно получим

           = cosa„ = х., sin               уп sinesinqj+ cose.          

При этом каждую компоненту результирующего поля можно вычислить как

           Ё = Ел (6, ф)             КОЕ exp[i К(хп sin ecosp +

(1.24) + уп sinesinp+ z„ cosB)] .

Описанные выше излучающие системы из идентичных элементов носят название антенных решеток (АР) и широко применяются в антенной технике для увеличения направленности излучения. Из выражения (1.24) видно, что для АР диаграмма направленности всей излучающей системы, т.е. зависимость напряженности поля от угловых координат, определяется для каждой из компонент выражением