Исследование неоднородностей в прямоугольном волноводе. Реактивные диафрагмы и резонансное окно в прямоугольном волноводе. Критическая длина волны

ЛАБОРАТОРНАЯ РАБОТА  №2

Исследование неоднородностей в прямоугольном волноводе

1. Цель работы: экспериментальная проверка основных положений теории волновода, измерение полных проводимостей различного типа неоднородностей, сравнение данных эксперимента с расчетными.

2. Основные теоретические положения

2.2. Реактивные диафрагмы и резонансное окно в прямоугольном волноводе

Как известно, распространение волн по волноводу постоянного сечения характеризуется фазовой постоянной  и длиной волны в волноводе , определяемыми для каждого типа волн из соотношений:

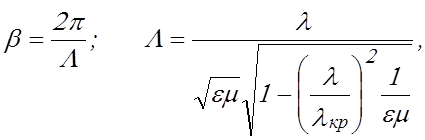                  (2.1)

где - длина волны в свободном пространстве (-генератора), - критическая длина волны для данного волновода.

В случае волновода прямоугольного сечения  для всех типов волн:

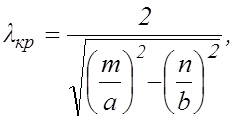                               (2.2)

где  и  поперечные размеры волновода, числа  и , указывающие число вариаций поля по размерам поперечного сечения, определяют тип волны. Для волн ТМ(Е)  = 1, 2, 3,...,  = 1, 2, 3,..., для волн ТЕ(Н)  = 0, 1, 2,...,  = 0, 1, 2,... .

Основным (низшим) типом волны в прямоугольном волноводе является волна Н₁₀ с λ_кр=2а . Характеристическое сопротивление волновода на волне Н₁₀ при воздушном заполнении определяется:

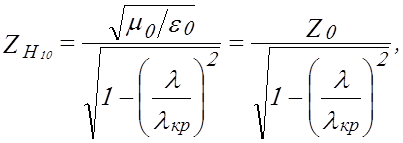                       (2.3)

где  - сопротивление свободного пространства, равное 376,7 Ом.

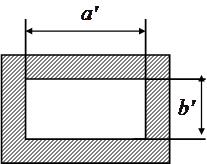
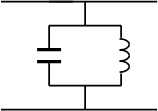
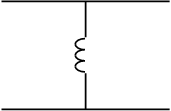
В технике СВЧ часто возникает необходимость введения в волновод тех или иных неоднородностей. Простейшими из них являются реактивные диафрагмы: ёмкостная (рис. 2.1а) и индуктивная (рис. 2.1б) - тонкие идеально проводящие перегородки, частично перекрывающие сечение волновода.

в)

а)

б)

Рис. 2.1. Ёмкостная(а), индуктивная (б) диафрагмы и резонансное окно (в) в прямоугольном волноводе

На рис 2.1. также указаны схемы замещения этих неоднородностей, на которых волновод представлен в виде бесконечной линии. Теория, учитывающая высшие типы волн, существующие вблизи любой неоднородности, дает следующие выражения для расчета реактивных проводимостей тонких симметричных диафрагм в относительных единицах: а) ёмкостной 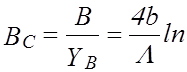        cosec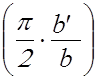отн. ед.,                     (2.4)

б) индуктивной 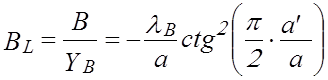   отн. ед.,                      (2.5)

где  - проводимость основного волновода.

Для удобства практического применения эти выражения приводятся в литературе в виде графиков [1].

Сочетание индуктивной и ёмкостной диафрагм при определенном соотношении  и  образует резонансное окно (рис. 1в), через которое волна проходит без отражения. Возможное соотношение между  и  можно определить следующим образом. Представим резонансное окно в виде бесконечно короткого волновода длиной, равной толщине диафрагмы, с размерами поперечного сечения   и , включенного в основной волновод. Для передачи энергии без отражения необходимо равенство эквивалентных сопротивлений основного волновода и волновода, замещающего резонансное окно:

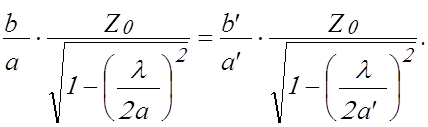         (2.6)

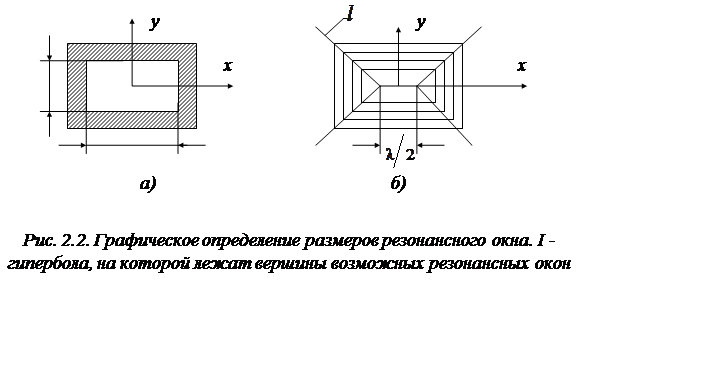
Выбрав прямоугольную систему координат и введя обозначения ,  (рис. 2.2а), преобразуем уравнение (2.6):

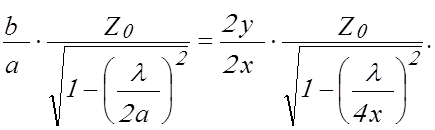        (2.7)

После несложных преобразований уравнения (2.7) получим уравнение гиперболы

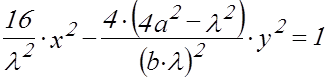.                        (2.8)

Продольная ось гиперболы равна . Таким образом, минимальные размеры резонансного окна равны:  , а максимальные:  . Остальные возможные значения   и  для данного значения  определяются графически (рис. 2.2б).

И обратно, из выражения (2.6) можно получить значение , если размеры окна известны:

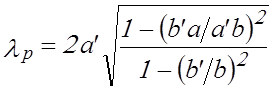.                       (2.9)

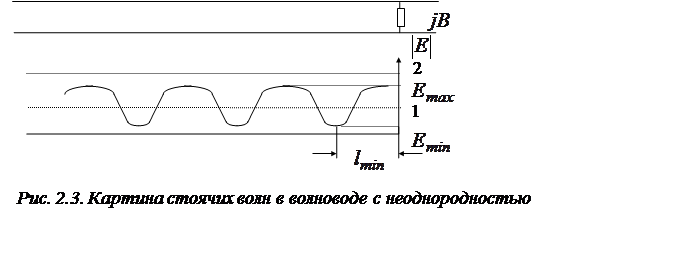
Из рис. 2.1 видно, что рассмотренные выше неоднородности включаются в основной волновод как шунтирующие реактивности, проводимость которых зависит от размеров неоднородностей.

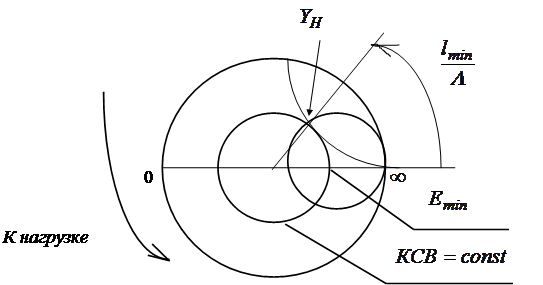
Определить полную проводимость любой неоднородности экспериментально проще всего с помощью измерительной линии и круговой диаграммы полных проводимостей. Достаточно определить  и расстояние от этой неоднородности до точки ближайшего минимума стоячей волны напряженности электрического поля E (рис. 2.3).

Располагая этими двумя величинами ( и ), с помощью круговой диаграммы полных проводимостей легко определить проводимость неоднородности (рис. 2.4). Описание круговой диаграммы дано в [1]. Рассмотрим подробнее методику определения  и .

		Рис. 2.4. Определение проводимости нагрузки YH по известным  и

2. Определение

Непосредственное определение (измерение) расстояния от неоднородности до ближайшего минимума напряженности поля не всегда практически осуществимо, например, при очень короткой длине волны и при наличии переходов между измерительной линией и неоднородностью. Указанное затруднение обычно обходят с помощью опыта короткого замыкания неоднородности, поясняемого на рис. 2.5. При коротком замыкании неоднородности фиксируется положение одного из минимумов напряженности Е, находящегося в пределах рабочего участка измерительной линии z* (условный конец линии). Затем к линии подключается неоднородность и находится положение минимума напряженности Е, ближайшего к ранее найденному со стороны генератора . Расстояние между найденными положениями минимумов в точности равно расстоянию от неоднородности до ближайшего минимума =. Поскольку на диаграмме полных проводимостей необходимо откладывать  , то  можно непосредственно определить из описанного выше опыта короткого замыкания как удвоенное расстояние между двумя соседними минимумами стоячей волны.