Основы строгого решения задачи о симметричном электрическом вибраторе. Разность потенциалов. Интегральное уравнение Галлена

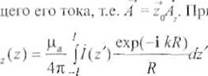интегрального .',ракнепия  выводе уравнения •аллена из следующей элек [годинамической модели задачи, 1] рсдлолагае•гея, вибратора много меньше как длины волны А., так плеча В силу расчете поля можно пренебречь лорис•выми токами л считагь, что боковой поверхности вибратора имеет только сосглвл•моповерхностной плотностыо которая обрагттается в пуль пл концах Излучение тока заменяется излучением тактмо же тока, но по бесконечно тонкой нити, совпадающей с осью : (см. рис. 2.1). осевой ток 1 причем /(::) = 2ttLJ(z). Электрическое поле, соданным током, можно вычислить через векторный потенциал А , кокак известно [18], имеет •ыкие же компоненты, как плотносп, иотока, т.е. Л При линейном распределении лока

(2.22)

координата точки набуноленпн (точка, н которой определяется лекторныЙ потенциал); — координата иптсјгирования; Л =

— расстояние между точкой наблюдения ЗАјчкол ин тс] гировагтия. Напряженность электрического поля связана с вектором А известным соотношением

                                            grad div Й.                                                              (2.23)

Поскольку А то ташенциальная к плечам вибратора компонента элек-тическон» поля

                                                                            (2.24)

Полагая, что вибратор выполнен идеально:х» проводника, на поверхности кторон» выподняегся танинное условие Е = О (где Е — касательная вектора Е), из (2.24) получаем, что во всех точках на боковой поверхности плеч вибратора

                                                                                              (2.25)

При выводе (2.25) подразумевается, чло величина Е, определяемся только излучением тока те. нс учитывается пренебрежимо малое собственное излучение устройслва, возбуждаюи1С[0 вибратр.

Связь векторного 11(угенциала А с прило.женным к вибратору в зазоре напряжением может быть установлена через скалярный потенциал (В связанный с А условием калибровки [18], которое в точках на поверхности вибратора имссг вид

                        (45 = i                                                                           (2.26)

Ввиду малости зазора, к которому подводится питающее напряжение, МОЖНО считать, что разность потенциалов

(2,27)

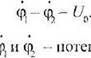            где           — потенциалы в точках 1 л 2 (см. рис. 2.1).

Решение уравнения (2.25) можно представить в виде

(2.28)

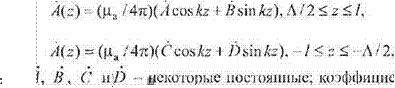коэффилиепт »„/47( введен для удобства дальнейших преобразований, В силу симметрии задачи С А, D —

Й(д) — (уга ; cosk:-F —l /, (2.29) Постоянную В найдем из условия (2,27), 110!1агая —) О:

                                          00.                                                                         (2,30)

С учетом (2.29) и (2.30) получим интегральное уравнение Галлена

                         R]dz' Й cosk; — i(27i/             sink •z             (2.31)

Постоянная Л определяется из условия обращения в нуль тока на копцах тггснлы е

Решения уравнения (2.31) в аналитическом виде нс существует. Паиболее распространены численные методы решения уравнения аллсиа, например ,ме'јод моментов. Суп, метода сводится к следующему. Искомую функшпо распределения тока I(z) представляют в виде разложения в ряд по некоторой системе функций (с неизвестными тэффлциензами), носящих название базисных, причем каждая из базисных функций может представлять распределение тока как по всей длине вибралјра, так и (Ујрезкам, на кото-