ПОСТРОЕНИЕ ГРАФИКОВ В EXCEL (1 часть курсовой работы)
1. в правой прямоугольной декартовой системе координат
В декартовых координатах каждому значению аргумента x, определенному в интервале задания функции, ставится в соответствие значение функции y, вычисляемое по заданной зависимости: y y(x), x[x1, x2], аргумент x меняется в интервале от х1 до х2, шаг изменения аргумента равен х. Результаты расчетов отобразить на точечной диаграмме. Приведенная в каждом варианте диаграмма графика функции в плоскости X-Y позволяет оценить корректность проведенной работы.
|
|
|
|
|
|
|
|
|
|
Вариант 7
|
|
|
Вариант 9
|
Вариант 10
|
2. функции, зависящие от параметра
В Ошибка! Источник ссылки не найден. заданы параметрические уравнения функций х= х(t), у= у(t), интервал изменения параметра t и шаг изменения параметра t, он равен t. Табулировать функции х= х(t) и у= у(t), результаты расчетов отобразить на точечной диаграмме в плоскости X-Y. Приведенная в каждом варианте точечная диаграмма графика функции в плоскости X-Y позволяет оценить корректность проведенной работы.
|
Вариант 1 t(3 t2) x
3 y t2 |
, 10t 6, t 0,3 |
|
|
Вариант 2 x t sint y
t cost 0t
2, t
, |
|
||
|
Вариант 3 t (3t2) x 3
y t2 , 0t , t 50 |
|
||
|
Вариант 4. x tg t
, y sin 2t 2cos 2t |
t
50 |
|
|
|
Вариант 5 x sin 2 t 0t 2, 2 , y t |
t 30 |
|
|
|
Вариант 6 x et cos t t y e sin t , 0t , |
t
50 |
|
|
3. функции, заданные уравнениями в полярных координатах
В таблице задано уравнение функции в полярных координатах = (), интервал изменения параметра и шаг изменения параметра , он равен . Табулировать функции х=x(,) и y=y(,), результаты расчетов отобразить на точечной диаграмме в плоскости X-Y. Для проверки корректности проведенных расчетов приведена точечная диаграмма графика функции в плоскости X-Y.
|
Вариант 1 2 b2 1 cos : 0
2,
30 |
|
|
|
Вариант 2 2 b2 1 cos : 5,25
6,8 ,
30 |
|
|
|
Вариант 3 2b cos 1cos : 7,3 8,56 |
b 7 ,
60 |
|
|
Вариант 4 1
a
: 0,1
3,14 ,
60 |
|
|
|
Вариант 5 2 a2cos2, a7 : 0
2
,
60 |
|
|
|
3 :[0, 2], , , 2 2 30 |
|
|
|
Вариант 7
:[0, 2], , , 2 2 30 |
|
|
|
Вариант 8 a(1 cos), a 0,3 , : 0
2,
30 |
|
|
|
Вариант 9 l a sin, l 3, a 6 , : 0
2,
|
|
|
|
Вариант 10 b acos, a 12, b 6, : 0
2,
30 |
|
|
4. построение нескольких кривых на одной диаграмме
В уравнение функции, заданное в условии задания, входят несколько коэффициентов. Определены значения коэффициентов. Для каждого варианта значения коэффициентов построить таблицу значений функции – ряд данных. Результаты расчетов отобразить на одной точечной диаграмме в
плоскости X-Y. Шаг
табулирования ![]() .
30
.
30
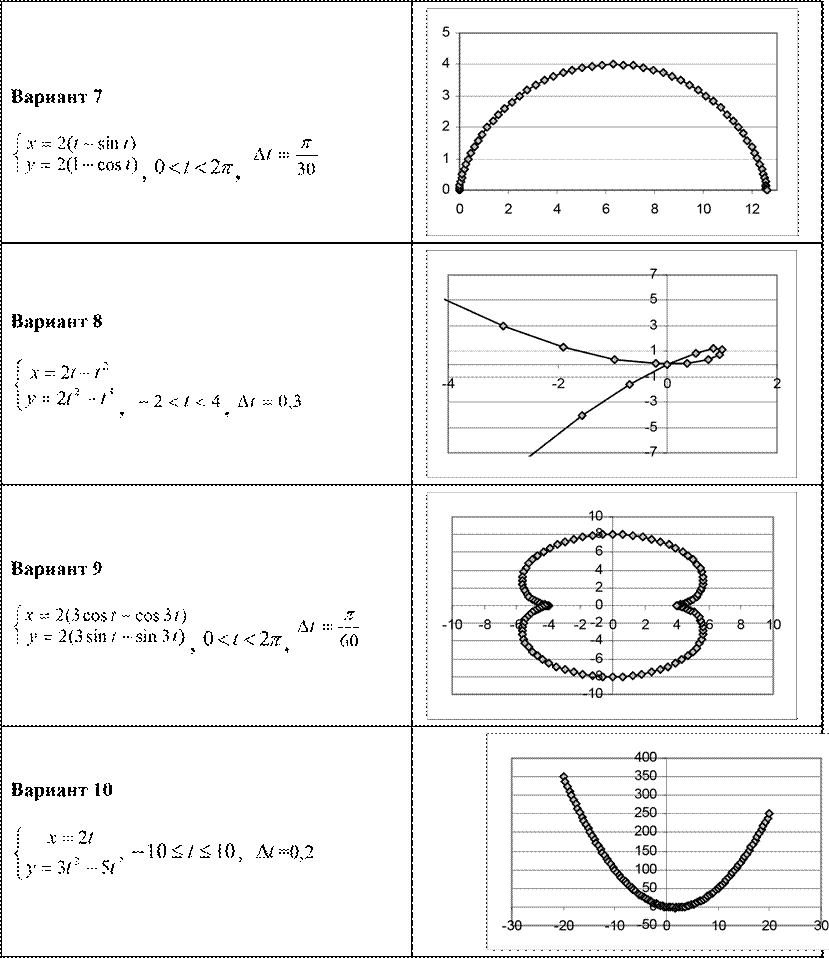
Вариант 1. Кривая задается параметрическими уравнениями:
x acos3t
y (acost b)sin t , где 0 t 2.
Рассчитать ряды значений х и y для каждого варианта значений параметров a и b:
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
|
a |
0,1 |
0,5 |
0,8 |
1,5 |
2 |
4 |
|
b |
0,5 |
1,5 |
1 |
2 |
1 |
2,5 |
Результаты расчетов отобразить на точечной диаграмме в осях X-Y.
Ответ:
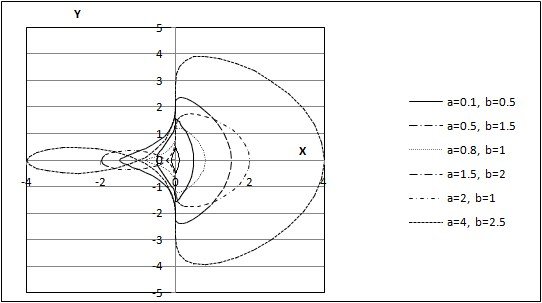
Вариант 2. Пусть на круг, описанный из центра ()О, радиусом а, навернута по часовой стрелке нить. Нить разматывается против часовой стрелки, конец ее все время натягивается. Кривая, описываемая этим концом нити, называется эвольвентой круга. Она представляется следующими параметрическими уравнениями:
x a ( t s i n t c o s t )
, где 0 t 2.
y a ( s i n t c o s t )
Параметр a принимает следующие значения:
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
|
a |
0,3 |
0,8 |
1,3 |
1,5 |
2 |
2,5 |
Рассчитать ряды значений х и y для каждого варианта значения параметра a. Результаты расчетов отобразить на точечной диаграмме в осях X-Y.
Ответ:
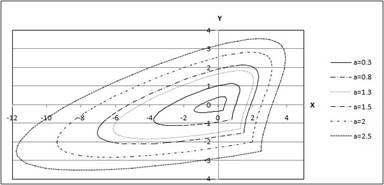
3. Кривая задается уравнением в полярных координатах:
a sin( b ) ( a b ), : 0 2.
Параметров a и b принимают значения:
|
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
a |
0,9 |
0,8 |
2 |
1 |
1,3 |
1,5 |
|
b |
0,3 |
0,1 |
0,8 |
0,5 |
0,5 |
0,5 |
Табулировать функцию ρ, рассчитать ряды значений х и y для каждого варианта значений параметров a и b. Результаты расчетов отобразить на точечной диаграмме в осях X-Y. Ответ:
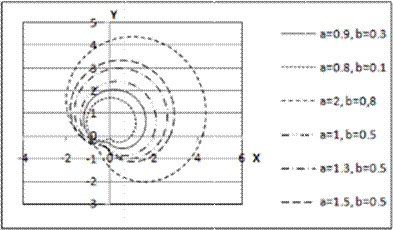
Вариант 4. Кривая “Овалы Кассини” задается параметрическими уравнениями:

x
cos t
cos t
, где
x
cos t
cos t
, где
![]() t
t ![]() .
.
y cos t sin t 2 2
Параметр a принимает следующие значения:
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
|
a |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
1 |
Рассчитать ряды значений х и y для каждого варианта значения параметра a. Результаты расчетов отобразить на точечной диаграмме в осях X-Y.
Ответ:
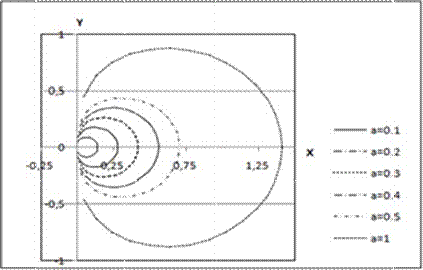
5. Кривая задается параметрическими уравнениями:
x a cos3 t
3 , где 0 t 2.
y a sin t
Параметр a принимает значения:
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
|
a |
1 |
2 |
3 |
4 |
5 |
6 |
Рассчитать ряды значений х и y для каждого варианта значения параметра a. Результаты расчетов отобразить на точечной диаграмме в осях X-Y.
Ответ:
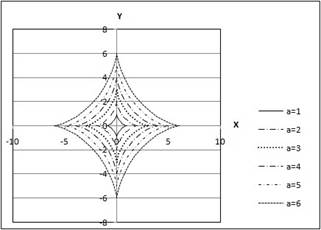
Вариант 6. Кривая задается параметрическими уравнениями:
x acos3 t
3 , где 0 t 2.
y asin t a
Параметр a принимает значения:
|
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
a |
1 |
2 |
3 |
4 |
5 |
6 |
Рассчитать ряды значений х и y для каждого варианта значения параметра a. Результаты расчетов отобразить на точечной диаграмме в осях X-Y.
Ответ:
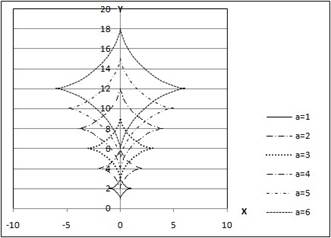
7. Значения функции y определяются по формулам:
![]()
y ax1, при 0x 2 ,
sinxb, при ![]() x 6
x 6
2
значение параметра b определяется по формуле: b
![]() а . 2 Параметр a принимает
значения:
а . 2 Параметр a принимает
значения:
|
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
a |
3 |
4 |
5 |
6 |
7 |
8 |
Рассчитать ряды значений х и y для каждого варианта значения параметра a. Результаты расчетов отобразить на точечной диаграмме в осях
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.