Электротехника \ Электротехника

Расчет разветвленной цепи постоянного тока. Метод последовательного применения законов Кирхгоффа, метод контурных токов и метод узловых потенциалов, страница 2

u2=u1+E1=0+12=12В; u3=u2-I1*R1=12+2,883*2=17,766В; u4=u3-E3=17,766-30=-12,234В; u5=u4+I3*R3=-12,234+2,803*6=4,584В;

u1=u5+I6*R6=4,584-0,574*8=0


 2

разветвленной цепи переменного тока с одним источником методом

эквивалентных преобразований. По результатам расчета составляется баланс мощностей, строится потенциальная диаграмма.

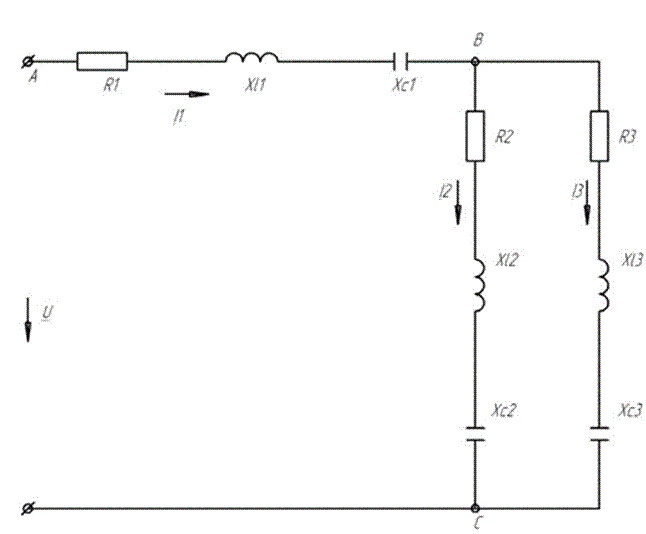
Дано:

U =В;

Uab =В;

Ubc = 810В;

I1= А;

I2 = А;

I3 = А;

R1= 5Ом;

R2 = 7Ом;

R3 = 6Ом;

Xl1= 0Ом;

Xl2 = 3Ом;

Xl3 = 0Ом;

Xc1= 6Ом;

Xc2 =Ом;

Xc3 =Ом

Решение:

7.  Определение комплексных сопротивлений ветвей

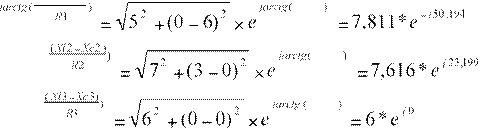
(Xl1−Xc1)

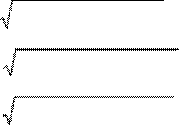Z1= R12 + (Xl1− Xc1)2 ×e

jarctg( 2   2

Z2 = R2 + (Xl2 − Xc2) ×e

jarctg( 2   2

Z3 = R3 + (Xl3− Xc3) ×e

8.  Полное сопротивление цепи

Z2 + Z3   7 + 6 + j(3− 0 + 0 − 0)                 j10,204

Z23 =             =             j23,199                    j0 = 3,425*e         

Z2*Z3       7,616*e          *6*e

Z = Z23+ Z1= 3,371+ j0,607 + 5− j6 = 9,958*e− j32,794

9.  Определение токов и напряжений в ветвях

Принимаем фазовый угол ϕUbc = 0

Ubc         810*e j0                                             − j23,199

I2 =        =              j23,199 =106,355*e           ;

Z2      7,616*e

Ubc     810*e j0                            j0

I3 =        =           j0 =135*e

Z3        6*e

I1= I2 + I3 = 97,755− j41,896 +135 = 232,755− j41,896 = 236,5*e− j10,204 U = I1*Z = 236,5*e− j10,204 *9,958*e− j32,794 = 2355,067*e− j42,998 ;

Uab =U −Ubc =1722,443− j1606,1−810 = 912,443− j1606,1=1847,2*e− j60,399

10.  Баланс мощностей

Активная мощность

Pист=U * I1*cos(ϕU −ϕI1) = 2355,067*236,5*cos(−42,998 +10,204) = 468,204кВт

Pпотр=∑I 2 * R = I12 *R1+ I22 * R2 + I32 *R3 = 236,52 *5 +106,3552 *7 +1352 *6 =

= 468,19кВт Реактивная мощность

Qист=U *I1*sin(ϕU −ϕI1) = 2355,067*236,5*sin(−42,998+10,204) =−301,668кВар

Qпотр=∑I 2 *(Xl − Xc) = I12 *(Xl1− Xc1) + I22 *(Xl2 − Xc2) + I32 *(Xl3− Xc3) =

236,52 *(0 − 6) +106,3552 *(3− 0) +1352 *(0 − 0) =−301,659кВар

 3

цепи переменного тока с двумя узлами методом двух узлов. По результатам

расчета составляется баланс мощностей. Дано:

E1= 40e− j60 В;

E2 = 81e j0 В;

E3 = 20e j0 В;

R1= 5Ом;

R2 = 7Ом;

R3 = 6Ом;      

Xl1= 0Ом;

Xl2 = 3Ом;

Xl3 = 0Ом;

Xc1= 6Ом; Xc2 =Ом;

Xc3 =Ом

Решение:

11. 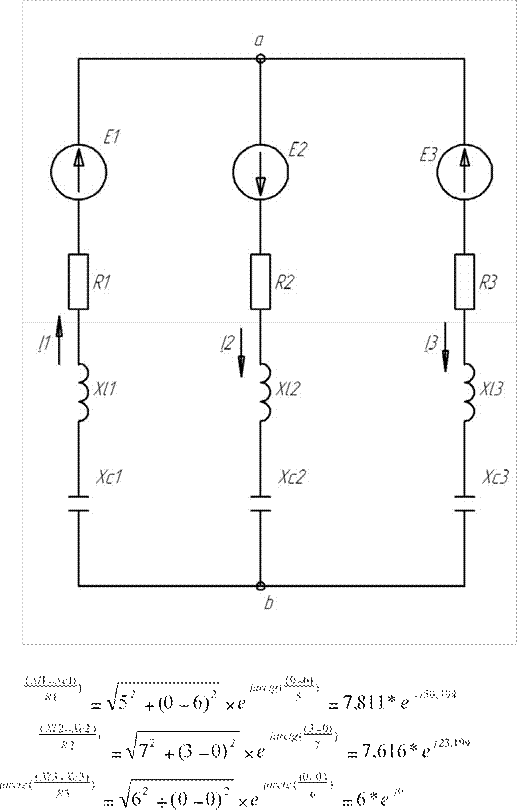 Определение комплексных сопротивлений ветвей

jarctg(

Z1= R12 + (Xl1− Xc1)2 ×e

jarctg(

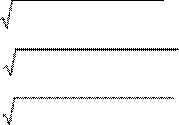Z2 = R22 + (Xl2 − Xc2)2 ×e

Z3 = R32 + (Xl3− Xc3)2 ×e

12.  Проводимости ветвей

G1=1/ Z1=1/7,811*e− j50,194 = 0,128*e j50,194 ;

G2 =1/ Z2 =1/7,616*e j23,199 = 0,131*e− j23,199 ;

G3 =1/ Z3 =1/6*e j0 = 0,167*e j0

13.  Узловое напряжение

E1*G1− E2*G2 + E3*G3

Uab = =

G1+G2 +G3

40*e− j60 *0,128*e j50,194 −81*0,131*e− j23,199 + 20*0,167*e j0

=                        j18,435                               − j37,875                               j39,806                        =

0,063*e          + 0,088*e           + 0,128*e

== 9,668*e j105,623

14.  Токи в ветвях

I1 = (E1−Uab)*G1 = (20 − j34,641+ 2,604 − j9,311)*0,128*e j50,194 = 6,328*e− j12,590 ;

I2 = (E2 +Uab)*G2 = (81+ 2,604 − j9,311)*0,131*e− j23,199 =10,366*e− j16,425 ;               

I3 = (−E3+Uab)*G3 = (−20 + 2,604 − j9,311)*0,167*e j0 = 4,074*e j157,612 ;

15.  Баланс мощностей

Активная мощность

Pист= E1*I1*cos(ϕE1 −ϕI1) + E2*I2*cos(ϕE2 −ϕI 2 ) − E3*I3*cos(ϕE3 −ϕI3 ) =

= 40*6,328*cos(−60 +12,59) +81*10,366*cos(0 +16,425) + 20*4,074*cos(0 −157,612) =

=1052,048Вт                                                                                                                  

Pпотр=∑I 2 *R = I12 *R1+ I22 *R2 + I32 *R3 = 6,3282 *5+10,3662 *7 + 4,0742 *6 =

=1052,048Вт

Реактивная мощность

Qист= E1*I1*sin(ϕE1 −ϕI1) + E2* I2*sin(ϕE2 −ϕI 2 ) − E3* I3*sin(ϕE3 −ϕI3 ) =

= 40*6,328*sin(−60 +12,59) +81*10,366*sin(0 +16,425) + 20*4,074*sin(0 −157,612) =

= 82,111Вар                                                                                                                       

Qпотр=∑I 2 *(Xl − Xc) = I12 *(Xl1− Xc1) + I22 *(Xl2 − Xc2) + I32 *(Xl3− Xc3) =

6,3282 *(0 − 6) +10,3662 *(3− 0) + 4,0742 *(0 −5) = 82,111Вар

 4

трехфазной цепи при соединении потребителей звездой с учетом заданной в

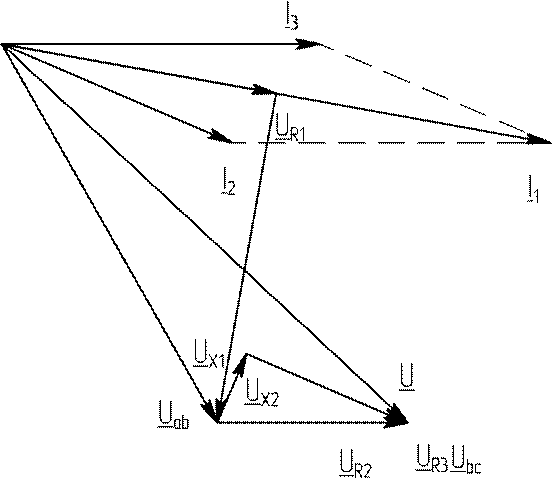
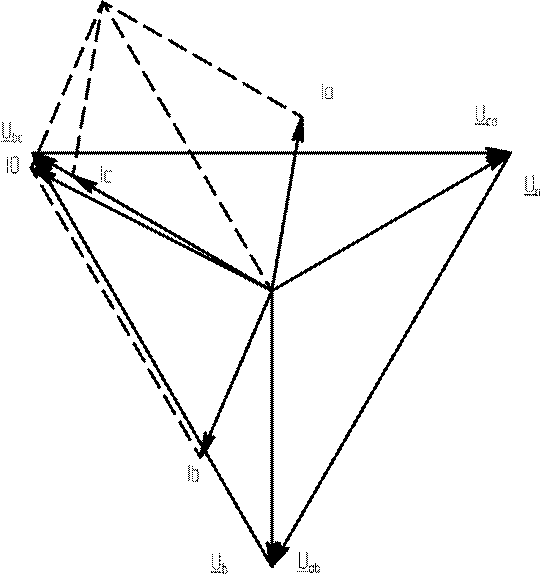
исходных данных начальной фазы фазного напряжения. По результатам строится векторная диаграмма токов и напряжений. Дано:

Uc = 81e j60 В;

R1= 5Ом;

R2 = 7Ом;

R3 = 6Ом;

Xl1= 0Ом;

Xl2 = 3Ом;

Xl3 = 0Ом;

Xc1= 6Ом;

Xc2 =Ом;

Xc3 =Ом

Решение:

16.  Определение комплексных сопротивлений ветвей

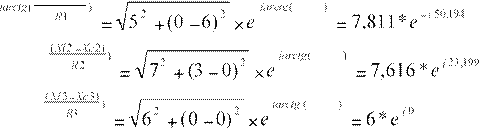
(Xl1−Xc1)

Z1= R12 + (Xl1− Xc1)2 ×e

jarctg( 2   2

Z2 = R2 + (Xl2 − Xc2) ×e

jarctg( 2   2

Z3 = R3 + (Xl3− Xc3) ×e

17.  Фазные напряжения

Ua = 81*e− j60 ;

Ub = 81*e j180

18.  Токи в ветвях

Ua          81*e− j60                                          − j9,806

Ia =      =             − j50,194 =10,371*e          А;

Z1     7,811*e

Ub         81*e j180

Ib = = j23,199 =10,636*e j156,801 А; Z2   7,616*e

Uc     81*e j60                             j60

Ic = = j0 =13,5*e А Z3 6*e

19.  Ток в нейтральном проводе

I0 = Ia + Ib+ Ic =10,219 − j1,766 −9,776 + j4,19 + 6,75+ j11,691=

j62,994

= 7,194 + j14,115 =15,842*e        А

Скачать файл