Расчет разветвленной цепи постоянного тока. Метод последовательного применения законов Кирхгоффа, метод контурных токов и метод узловых потенциалов

Пример 1

Расчет разветвленной цепи постоянного тока. Расчет производится тремя методами: методом последовательного применения законов Кирхгоффа, методом контурных токов и методом узловых потенциалов.

По результатам расчета составляется баланс мощностей, строится потенциальная диаграмма.

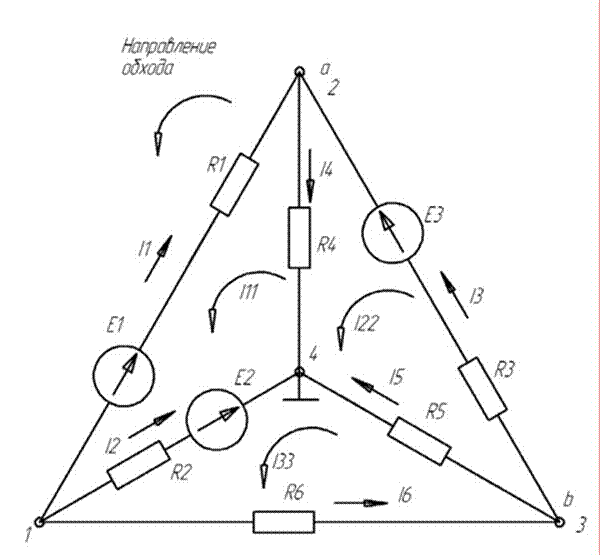Дано:

R1= 2Ом;

R2 = 2Ом;

R3 = 6Ом;

R4 = 4Ом;

R5 = 4Ом;

R6 = 8Ом;

E1=12В;

E2 = 25В;

E3 = 30В

Решение:

1. Определение токов в цепи непосредственным применением законов Кирхгоффа

⎧I1+ I3− I4 = 0;

⎪

I2 + I4 + I5 = 0;

⎪

⎪⎪I6 −I5−I3 = 0;

⎨                                                       

_⎪−I1*R1+ I2*R2 −I4*R4 =−E1+ E2;

⎪I5*R5−I2*R2 + I6*R6 =−E2;

⎪

⎪_⎩I4*R4 − I5*R5+ I3*R3 = E3

Решаем систему уравнений с помощью системы mathcad. Составим матрицу коэффициентов размерности a и вектор свободных членов  размерности b:

⎛ 1     0     1    −1   0    0 ⎞                                     ⎛ 0 ⎞

^⎜ 0     1     0     1     1    0                                         ^⎜ 0

⎜    ⎟                    ⎜         ⎟ _{a :=                            b :=} ⎜ 0 ⎟

⎜ 0     0    −1   0    −1 1 ⎟

⎜ −2   2     0    −4   0    0 ^⎟                                    ⎜ 13 ⎟

⎜                          ⎟                               ⎜      ⎟

0    −2   0     0     4    8                                          −25

⎜                                                          ⎜

⎝ 0     0     6     4    −4 0 ⎠                                     ⎝ 30 ⎠

Коэффициенты в матрице соответствуют коэффициентам при неизвестных в исходных уравнениях.

Решением получаем вектор неизвестных решений

⎛ −2.883⎞     

^⎜ 3.456            

⎜ 2.803 ⎟⎟          

⎜

X1 =

⎜ −0.08 ⎟

⎜         ⎟     

−3.376          

⎜

⎝ −^0.573⎠          где:

I1 =−2,883А;

I2 = 3,456А;

I3 = 2,803А;

I4 = −0,08А;

I5 =−3,376А;

I6 = −0,573А

2. Определение токов в цепи методом контурных токов

Составим систему уравнений для контурных токов

⎧I11*(R1+ R2 + R4) − I33*R2 − I22*R4 =−E1+ E2;

⎪

⎨I22*(R4 + R5+ R3) − I11*R4 − I33*R5 = E3;             

^⎪⎩I33*(R5+ R2 + R6) − I11*R2 − I22*R5 =−E2

Составим матрицу коэффициентов размерности d и вектор свободных членов  размерности f:

⎛ 8     −4 −2 ⎞ ⎜ d :=     −4 14 −4 ⎜ ⎝ −2 −4 14 ⎠

⎛ 13 ⎞ f := 30   ⎜ ⎜               ⎝ −25⎠

Решением получаем вектор неизвестных решений

⎛ 2.883 ⎞         

X2 = ⎜ 2.803                  

⎜ −0.573⎠         

⎝

где:

I11 = 2,883А;

I22 = 2,803А;

I33 =−0,573А;

Определим токи в ветвях:

I1=−I11=−2,883А;

I2 = I11− I33 = 2,883+ 0,573 = 3,456А;

I3 = I22 = 2,803А;

I4 = I22 − I11= 2,803− 2,883 =−0,08А;

I5 = I33− I22 =−0,573− 2,803 =−3,376А;

I6 = I33 =−0,573А

3. Определение токов в цепи методом узловых потенциалов

Для составления уравнений методом узловых потенциалов мысленно заземляем узел b.

Определим проводимости в соответствии с принятой нумерацией узлов (см. рис.):

G11=1/ R1+1/ R2 +1/ R6 =1/ 2 +1/2 +1/8 =1,125См;

G22 =1/ R1+1/ R4 +1/ R3 =1/ 2 +1/4 +1/6 = 0,917См;

G33 =1/ R6 +1/ R5+1/ R3 =1/8+1/4 +1/6 = 0,542См;

G12 = G21=−(1/ R1) =−1/2 =−0,5См;

G13 = G31 =−(1/ R6) =−0,125См;

G23 = G32 =−(1/ R3) =−1/6 =−0,167См

Определим узловые токи:

J11=−E1/ R1−E2/ R2 =−12/2 − 25/2 =−18,5А;

J22 =E3/ R3+E1/ R1= 30/6 +12/2 =11См;             

J33 =−E3/ R3 =−30/6 =−5А

Составим систему уравнений для узловых потенциалов при u4=0

⎧G11*u1+G12*u2 +G13*u3 =J11;

⎪

⎨G21*u1+G22*u2 +G23*u3 =J22;

^⎪⎩G31*u1+G32*u2 +G33*u3 =J33

Составим матрицу коэффициентов размерности h и вектор свободных членов 

размерности k:
⎛ 1.125     −0.5    −0.125⎞ ⎜ h :=      −0.5     0.917 −0.167 ⎜ ⎝ −0.125 −0.167 0.542 ⎠	⎛ −18.5⎞        ⎜    k :=     11              ⎜                 ⎝ −5 ⎠

Решением получаем вектор неизвестных решений

⎛ −18.089⎞ X3 = ⎜ −0.325  

⎜ −13.497⎠        

⎝

здесь:

u1 =−18,089В; u2 =−0,325В; u3 =−13,497В

Определим токи в ветвях:

E1− (u2 −u1)   12 − (−0,325+18,089)

I1=                     =                               =−2,882А;

R1                              2

E2 − (u4 −u1)    25− (0 +18,089)

I2 =                      =                        = 3,456А;

R2                          2

E3− (u2 −u3)    30 − (−0,325+13,497)

I3 =                      =                                = 2,805А;

R3                               6

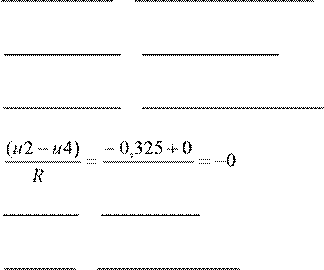I4 =,081А; 4   4

I5 =3,374А; 5 4

I6 =              =                         =−0,574А;

R6                      8

4.  Напряжение между точками a и b

Uab = u2 −u3 =−0,325 +13,497 =13,172В

5.  Баланс мощностей

Мощность источника

Pист= E1* I1+ E2* I2 + E3* I3 =−12*2,883 + 25*3,456 + 30*2,803 =135,894Вт

Мощность потребителя

Pпотр=∑I² *R = I1² *R1+ I2² *R2 + I3² *R3+ I4² *R4 + I5² *R5+ I6² *R6 =

= 2,883² *2 + 3,456² *2 + 2,803² *6 + 0,08² *4 + 3,376² *4 + 0,573² *8 =135,894Вт

Pист≈ Pпотр

6. Потенциальная диаграмма для внешнего контура.

Принимаем потенциал точки 1 равным 0. Далее в обходе по контуру по часовой стрелке: u1=0