
































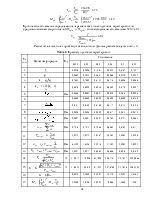















токе МДС в любой точке на статоре изменяется синусоидально во времени с амплитудою, равной FMK1X.
Т.е. значение МДС первой гармоники в любой момент
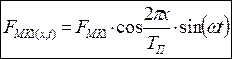
Причины возникновения высших гармоник магнитного поля.
Магнитное поле в воздушном зазоре асинхронной машины несинусоидальное. В нём, кроме основной гармонической, существует бесконечно большое число высших гармоник поля, которые принято разделять на пространственные и временные.
Пространственные гармоники появляются вследствие несинусоидальности распределения МДС в воздушном зазоре, обусловленной дискретным расположением проводников обмотки в пазах, и неравномерности самого воздушного зазора, вызванного наличием зубцов на статоре и роторе и рядом технологических факторов (эксцентричностью ротора и статора, конусностью ротора, эллипсностью зазора и др.). От основной гармоники поля высшие пространственные гармоники отличаются тем, что они имеют значительно меньшую амплитуду, другое число периодов и другие частоты вращения.
Высшие пространственные гармоники создают ряд добавочных моментов, действующих на ротор и оказывающих влияние на механическую характеристику двигателя. Эти моменты подразделяются на асинхронные, синхронные, вибрационные и реактивные.
Временные гармоники поля появляются при питании двигателя несинусоидальным напряжением, например при питании его от статического преобразователя частоты, когда к обмотке статора подводится напряжение прямоугольной формы, или при включении в цепь обмотки статора нелинейных элементов (нелинейных реакторов, вентилей и др.). В этих случаях токи фаз содержат наряду с основной гармоникой и высшие гармоники, каждая из которых имеет частоту fv=vf1 и создаёт такой же ряд пространственных гармоник, как и основные гармоники, но вращающиеся в v раз быстрее.
Гармоники, возникающие при питании двигателя несинусоидальным напряжением, создают добавочные асинхронные и колебательные моменты. Все виды высших гармоник (пространственные и временные) приводят к возникновению добавочных потерь мощности в обмотках и магнитопроводе машины.
33. Значения индукций:
В зубцах статора:
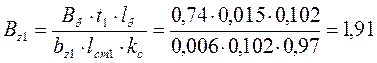 Тл
Тл
В зубцах ротора:
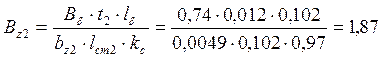 Тл
Тл
В ярме статора:
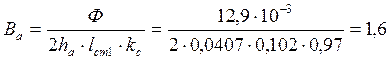 Тл
Тл
В ярме ротора:
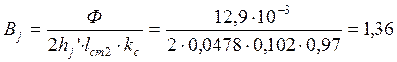 Тл
Тл
Расчетная высота ярма ротора:
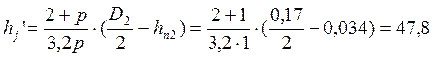 мм
мм
34. Магнитное напряжение воздушного зазора:
![]() А, где
kδ – коэффициент
воздушного зазора:
А, где
kδ – коэффициент
воздушного зазора:
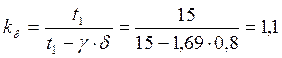
Коэффициент:
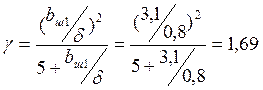
35. Магнитные напряжения зубцовых зон:
Статора:
![]() А, где
Нz - магнитная
напряженность поля в зубцах статора или ротора
А, где
Нz - магнитная
напряженность поля в зубцах статора или ротора
По приложению II (в соответствии с Bz), рис. П-17, с.461 [2]: при Bz1=1,91 Тл→Hz1=2160 А/м,
hz1=hп1=29,8 мм=0,0298 м
Ротора:
![]() А
А
При Bz2=1,87 Тл→Hz2=1890 А/м
![]() мм
мм
36. Коэффициент насыщения зубцовой зоны:
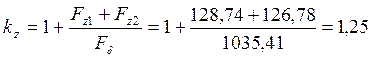
Коэффициент насыщения зубцовой зоны в пределах нормы, т.е. 1,2<kz<1,5 (с. 194 [2]).
37. Магнитные напряжения ярм статора и ротора.
![]() А
А
По табл. П-16, с. 470 [2], при Ba=1,6 Тл→Ha=750 А/м где Lа – длина средней магнитной линии ярма статора
На – магнитная напряженность поля при индукции Ва по кривой намагничивания для ярма принятой марки стали.
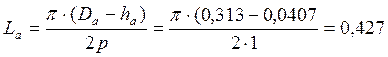 м
м
![]() А
А
По табл. П-16, с.460 [2], при Bj=1,36 Тл→Hj=365 А/м
Т.к. в проектируемом асинхронном двигателе 2p=2, то (с. 195)
![]() м
м
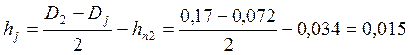 м где
Hj – магнитная напряженность поля при
индукции Bj по кривой намагничивания для ярма
принятой марки стали
м где
Hj – магнитная напряженность поля при
индукции Bj по кривой намагничивания для ярма
принятой марки стали
Lj – длина средней магнитной линии потока в ярме ротора
hj – высота спинки ротора
38. Магнитное напряжение на пару полюсов:
![]() А
А
39. Коэффициент насыщения магнитной цепи:
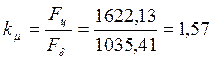
40. Намагничивающий ток.
 А
А
Относительное значение:

Относительное
значение намагничивающего тока в пределах нормы (с. 195 [2]),т.е. 0,18<![]() <0,2. Параметры машины выбраны
оптимально (довольно высокий КПД и cosj при не слишком высоком перерасходе материала).
<0,2. Параметры машины выбраны
оптимально (довольно высокий КПД и cosj при не слишком высоком перерасходе материала).
Параметры рабочего режима.
41. Активное сопротивление фазы обмотки статора:
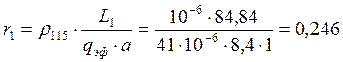 Ом
Ом
Для класса нагревостойкости F расчетная температура υРАСЧ=115 °С, для меди удельное сопротивление материала обмотки при расчетной температуре ρ115=10-6/41 Ом·м.
Общая длина эффективных проводников фазы обмотки:
![]() м
м
Средняя длина витка обмотки:
![]() м
м
Длина пазовой части катушек:
![]() м
м
Длина лобовой части катушек:
![]() м, где
kл – коэффициент,
берущийся в зависимости от числа полюсов машины и наличия изоляции в лобовых
частях, по табл.6-19, с.197 [2] kл=1,45 (при лобовых частях обмотки, изолированных лентой),коэффициент
вылета катушки kвыл=0,44
м, где
kл – коэффициент,
берущийся в зависимости от числа полюсов машины и наличия изоляции в лобовых
частях, по табл.6-19, с.197 [2] kл=1,45 (при лобовых частях обмотки, изолированных лентой),коэффициент
вылета катушки kвыл=0,44
Средняя ширина катушки:
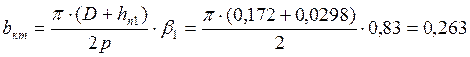 м, где
β1 – относительное укорочение шага обмотки, принимаем β1=0,83=5/6
м, где
β1 – относительное укорочение шага обмотки, принимаем β1=0,83=5/6
Считаем, что обмотка укладывается до запрессовки сердечника в корпус, тогда вылет прямолинейной части катушки из паза В=0,01 м (с. 197 [2]).
Длина вылета лобовой части катушки:
![]() м
м
Относительное значение:
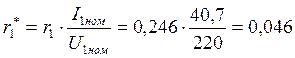
42. Активное сопротивление фазы обмотки ротора.
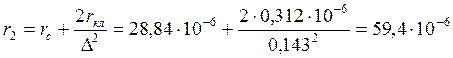 Ом
Ом
Активное сопротивление стержня обмотки:
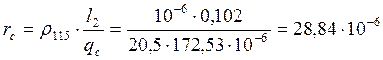 Ом
Ом
Активное сопротивление короткозамыкающего кольца:
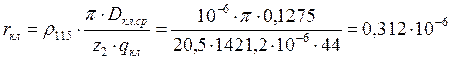 Ом
Ом
Для
литой алюминиевой обмотки ротора: 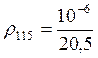 Ом·м
Ом·м
Приводим r2 к числу витков обмотки статора:
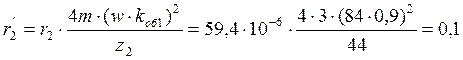 Ом
Ом
Относительное значение:
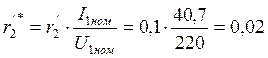 Ом
Ом
43. Индуктивное сопротивление фазы обмотки статора.
 Ом
Ом
lδ'=lδ=0,102 м т.к. радиальные вентиляционные каналы отсутствуют.
По табл. 6-22, с.200 (рис. 6.38 ж [2]):
Коэффициент магнитной проводимости пазового рассеяния:
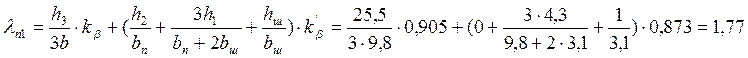
Значения коэффициентов kβ и kβ' определяют в зависимости от шага обмотки: при двухслойной обмотке с укорочением 2/3<β<1 (с.199 [2])
![]()
![]()
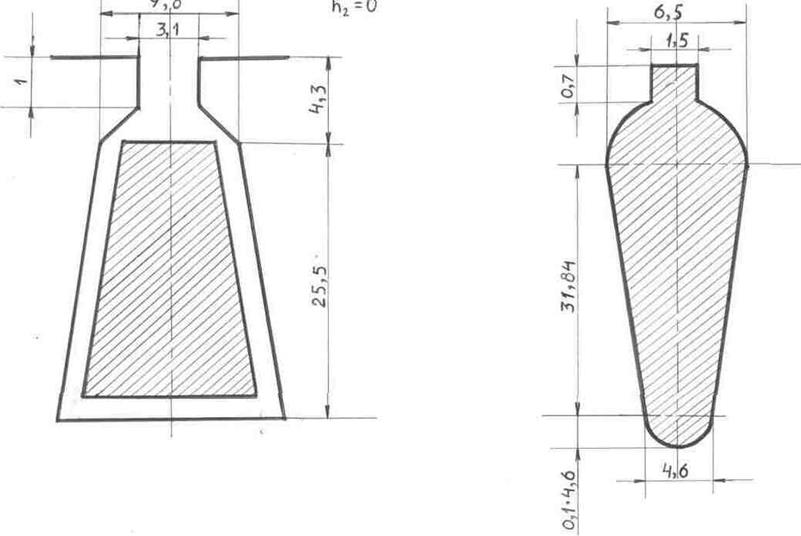
h1 паза статора=h3=25,5 мм
b=b2=9,8 мм
h2=0,
h1=hп1-h3=29,8-25,5=4,3 мм
Коэффициент магнитной проводимости лобового рассеяния:

Коэффициент магнитной проводимости дифференциального рассеяния:
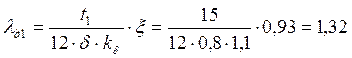
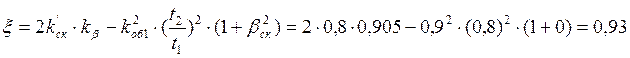
При
отсутствии скоса пазов статора или ротора т.е. для βск=0 и 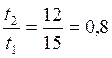 по рис. 6.39 д, с.201 [2]→коэффициент
скоса kск'=0,8
по рис. 6.39 д, с.201 [2]→коэффициент
скоса kск'=0,8
Относительное значение:
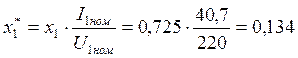
44. Индуктивное сопротивление фазы обмотки ротора.
![]() Ом
Ом
По табл. 6-23, с. 204, рис. 6-40 а [2]; для номинального режима kд=1 ( примечание к табл. 6-23 [2]).
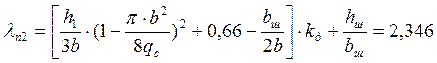
b=b1=6,5 мм
 мм
мм
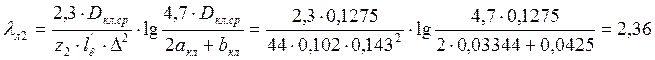

∆z – по рис. 6.39 а, с. 201 [2] при 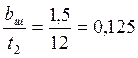 и
и 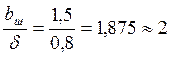 →∆z≈0
→∆z≈0
При большом числе пазов ротора, приходящихся на пару
полюсов (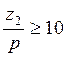 ) без заметной погрешности можно
принять (с.203 [2]):
) без заметной погрешности можно
принять (с.203 [2]):
![]()
![]()
Приводим x2 к числу витков статора:
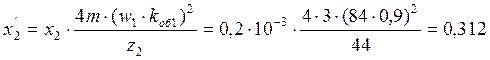 Ом
Ом
Относительное значение:
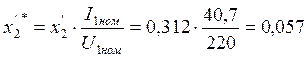
|
|
45. Потери в стали основные.
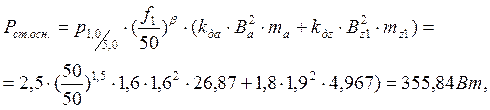
![]() -
удельные потери.
-
удельные потери.
Удельная масса стали γс=7,8·103 кг/м3 (с. 206 [2])
kда, kдz – коэффициенты, учитывающие влияние на потери в стали неравномерности распределения потока по сечениям участка магнитопровода и технологических факторов.
Для машин, мощностью меньше 250 кВт: kда=1,6, kдz=1,8 (с. 206 [2]).
Массы стали ярма и зубцов статора:
![]() = π·(0,313-0,0407)·0,0407·0,102·0,97·7,8·103=26,87
кг
= π·(0,313-0,0407)·0,0407·0,102·0,97·7,8·103=26,87
кг
![]() =
0,0298·0,006·36·0,102·0,97·7,8·103=4,967 кг
=
0,0298·0,006·36·0,102·0,97·7,8·103=4,967 кг
46. Поверхностные потери в роторе.
![]() Вт
Вт

где k02 – коэффициент, учитывающий влияние обработки поверхности головок зубцов статора или ротора, k02 принимаем равным 1,7 (с.207 [2])
![]()
для
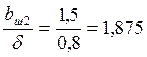 по рис. 6-41 [2], β02=0,1
по рис. 6-41 [2], β02=0,1
47. Пульсационные потери в зубцах ротора.
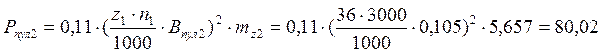 Вт
Вт
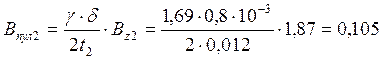 Тл
Тл
![]() кг
кг
hz2=hп2=34 мм
48. Сумма добавочных потерь в стали.
![]() Вт
Вт
49. Полные потери в стали.
![]() Вт
Вт
50. Механические потери.
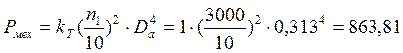 Вт
Вт
kТ=1 для двигателей с 2p=2 (c. 208 [2])
51. Добавочные потери при номинальном режиме.
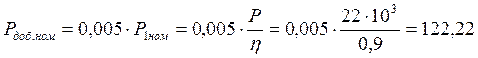 Вт
Вт
52. Холостой ход двигателя.
![]() А
А
Активная составляющая:
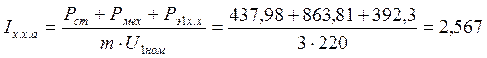 А
А
Реактивная
составляющая: ![]() =7,95 А (c. 209 [2], и п. 40 расчета).
=7,95 А (c. 209 [2], и п. 40 расчета).
Электрические потери в статоре при х.х.:
![]() Вт
Вт
Коэффициент мощности при х.х.:
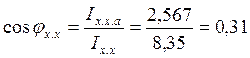
Расчет рабочих характеристик.
53. Параметры схемы замещения:
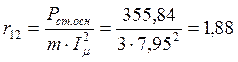 Ом
Ом
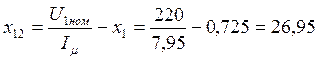 Ом
Ом
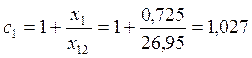
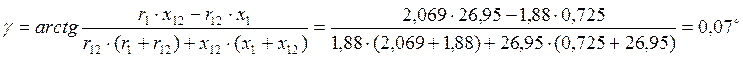 <1°
<1°
Активная составляющая тока синхронного холостого хода:
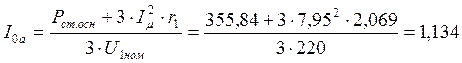 А
А
![]()
![]()
![]()
Потери, не меняющиеся при изменении скольжения:
![]() кВт
кВт
Принимаем Sном≈r2*=0,02 и рассчитываем рабочие характеристики, задаваясь S=0,005; 0,01; 0,015; 0,02; 0,025; 0,03; 0,035.
Данные расчетов представлены в табл.1.
Табл. 1. К расчету рабочих характеристик.
Данные спроектированного двигателя.
P2ном = 22 кВт; U1=220/380 В; 2p=2; I0a=0,61 A; I0p= Iμ =7,95 А; Pст+Pмех=1,3 кВт; r1=0,246 Ом; r2'=0,1 Ом ;c1 =1,027; a' =1,055; a =2,125 Ом ;b' =0; b =0,81 Ом ; I1н =40,7 А
|
№ п/п |
Расчётная формула |
Ед. |
Скольжение |
||||||
|
0,0050 |
0,0100 |
0,0150 |
0,0200 |
0,0250 |
0,0300 |
0,0350 |
|||
|
1 |
|
Ом |
21,1000 |
10,5500 |
7,0333 |
5,2750 |
4,2200 |
3,5167 |
3,0143 |
|
2 |
|
Ом |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
|
3 |
|
Ом |
23,2250 |
12,6750 |
9,1583 |
7,4000 |
6,3450 |
5,6417 |
5,1393 |
|
4 |
|
Ом |
0,8100 |
0,8100 |
0,8100 |
0,8100 |
0,8100 |
0,8100 |
0,8100 |
|
5 |
|
Ом |
23,2391 |
12,7009 |
9,1941 |
7,4442 |
6,3965 |
5,6995 |
5,2027 |
|
6 |
|
А |
9,4668 |
17,3217 |
23,9284 |
29,5532 |
34,3938 |
38,5998 |
42,2855 |
|
7 |
|
- |
0,9994 |
0,9980 |
0,9961 |
0,9941 |
0,9919 |
0,9898 |
0,9878 |
|
8 |
|
- |
0,0349 |
0,0638 |
0,0881 |
0,1088 |
0,1266 |
0,1421 |
0,1557 |
|
9 |
|
А |
10,5950 |
18,4204 |
24,9694 |
30,5117 |
35,2510 |
39,3420 |
42,9039 |
|
10 |
|
А |
8,2800 |
9,0547 |
10,0581 |
11,1657 |
12,3054 |
13,4357 |
14,5333 |
|
11 |
|
А |
13,4467 |
20,5256 |
26,9191 |
32,4906 |
37,3370 |
41,5729 |
45,2986 |
|
12 |
|
А |
9,7224 |
17,7894 |
24,5745 |
30,3511 |
35,3225 |
39,6420 |
43,4272 |
|
13 |
|
кВт |
6,9927 |
12,1575 |
16,4798 |
20,1378 |
23,2656 |
25,9657 |
28,3166 |
|
14 |
|
кВт |
0,1334 |
0,3109 |
0,5348 |
0,7791 |
1,0288 |
1,2755 |
1,5143 |
|
15 |
|
кВт |
0,0029 |
0,0053 |
0,0074 |
0,0091 |
0,0106 |
0,0119 |
0,0130 |
|
16 |
|
кВт |
0,0133 |
0,0311 |
0,0535 |
0,0779 |
0,1029 |
0,1275 |
0,1514 |
|
17 |
|
кВт |
1,4515 |
1,6491 |
1,8974 |
2,1678 |
2,4441 |
2,7167 |
2,9806 |
|
18 |
|
кВт |
5,5412 |
10,5083 |
14,5824 |
17,9699 |
20,8216 |
23,2490 |
25,3360 |
|
19 |
|
- |
0,7924 |
0,8644 |
0,8849 |
0,8923 |
0,8950 |
0,8954 |
0,8947 |
|
20 |
|
- |
0,7879 |
0,8974 |
0,9276 |
0,9391 |
0,9441 |
0,9463 |
0,9471 |
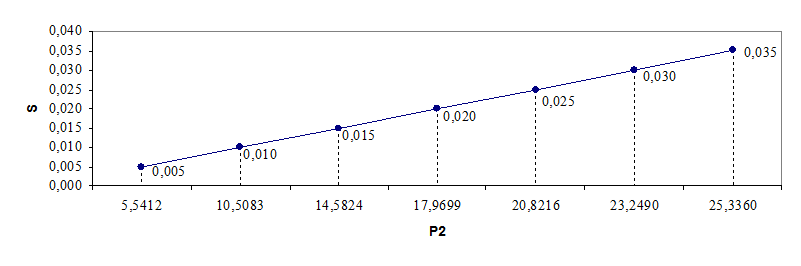
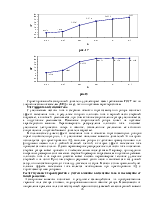
рис. 12
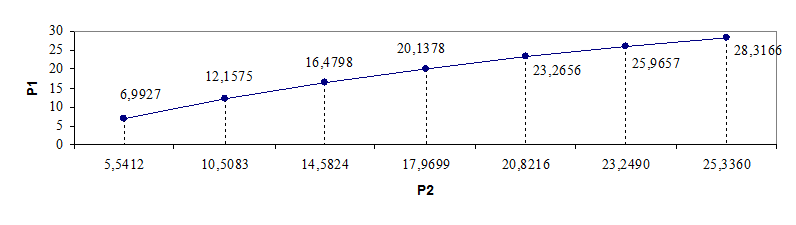
рис. 13
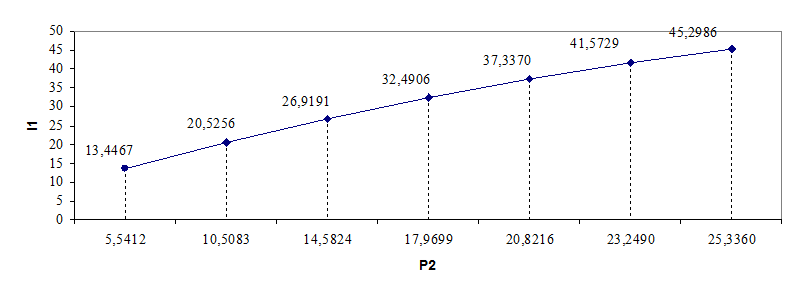
рис. 14
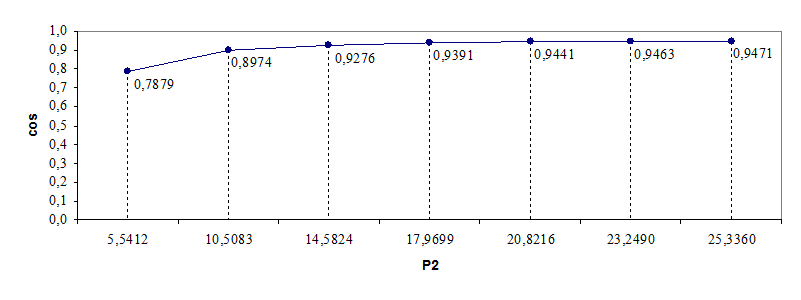
рис.15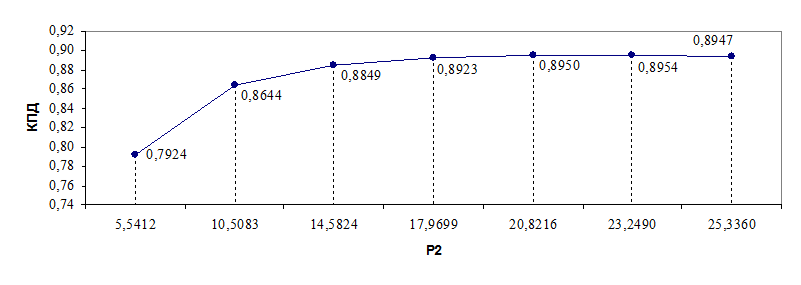
рис. 16
Расчет пусковых характеристик.
Параметры с учетом вытеснения тока при расчетной температуре υ=115°.
Приведенная высота стержня:
![]() , где
S – скольжение двигателя, данный расчет ведем для пуска
, где
S – скольжение двигателя, данный расчет ведем для пуска
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.