Подкласс Р-задачи, для кот. могут быть исп-ны полиномиальные алгоритмы kn2, lnn, n3. NP - для которых сущ-т только эксп. алгоритмы 2n, nn, n! n - объем исх. данных.
Эфф-ть алгоритма - max кол-во элементарных операций, вып. при его работе.
-множество ф-ий g(n) для кот. сущ-т константа С и такое no, для кот. |g(n)|<=c|f(n)|, n>=no
Если f(n) - по... ая ф-ия -> Р; экспоненциальная - NP.

В САПР применяются в основном Р-задачи.
Алгоритмы компоновки (алгоритмы покрытия и разрезания)
Различают алгоритмы из мн. прогр-ия, последовательные, итерационные.
Итерационные алгоритмы:
1. получение очередного варианта решения
2. Вычисление ф-ии критерия
3. Выбор лучшего варианта
4. Срабатывание правила останова (время, число итераций, улучш. становится меньше наперед заданной величины, перебор всех вариантов).
Особенность: в любой момент есть решение. Начальное решение получают с пом. послед. алгоритма, случайно и др.
Качество полученного решения зависит от качества начального.
Алгоритм разрезания:
G(X,U) разрезать на m частей:
G1(X1,U1), G2(X2,U2),....,Gm(Xm,Um)
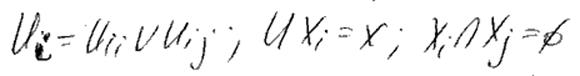
Алгоритм парных перестановок:
1) берем 2 куска: G1 и G2 , для каждой вершины выч. α;
αi-величина, кот. показывает, как изменится число внешних связей между 2мя кусками, если i-я вершина перейдет в др. кусок
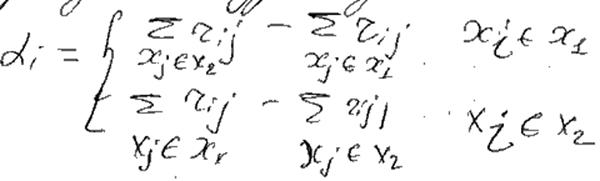
2)Для каждой пары из разных кусков выч. bij.
bij - как изменится число внешних связей, если 2 вершины (i и j) поменяются местами
bij=ai+aj-2rij
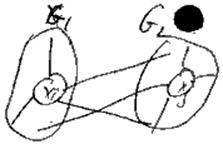
Если все bij<=0 - смысла переставлять вершины нет. Если есть bij>0, то выбирается max bij, вершины i и j меняются местами и процесс повторяют до тех пор, пока не рассмотрены все куски и при этом не было ни одной перестановки
Смешанный.
Рассматриваются не 2 отд. куска, а их комбиниции
Алгоритм размещения
-задача нахождения местоположения эл-ов на коммутационном поле, при кот. создаются наиболее благоприятные условия для соединений.
Критерии получения наиболее благоприятных условий эвристические
1)классический - суммарная длина соединений
2) максимальная длина соединения
3) число пересечений проводников
4) кол-во межслойных переходов
5) кол-во перегибов проводников
6) параметры связей между эл-ами
7)равномерность распределения проводников
8) равномерность распределения температуры по полю и т.д.
Алгоритмы размещения делят:
1) алгоритмы решения матем. задач, явл. моделями задач размещения
2) конструктивные алгоритмы начального размещения
3) итерационные алгоритмы улучшения начального размещ.
4) непрерывно-дискретные алгоритмы размещения
1. Алгоритмы решения мат. задач
Множество элементов
![]()
множество позиций
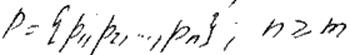
Связи между элементами
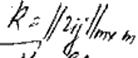
расстояние между позициями
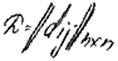
Евклидова метрика
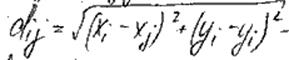
Ортогональная
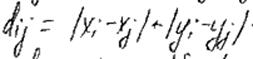

Метод ветвей и границ.
Все мн-во до. решений разбивается на подмножества. Для каждого из них вычисляется нижняя граница значения функционала: F(p)1, F(p)2, ... F(p)l; выбирается подмножество с меньшей нижней границей. Выбранное подмн-во делится на подмн-ва и т.д.. Все модификации отличаются способом разбиения на подмн-ва и способом выч нижн. гр.
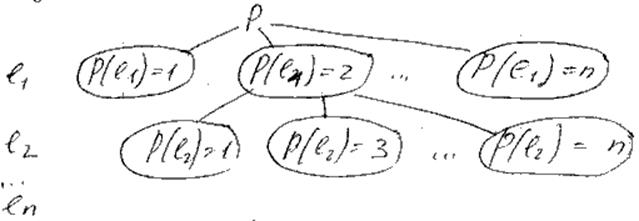
Для выч. нижней границы: (достигается, если один вектор упорядочен по невозрастанию, другой по неубыванию)
r = {r1, r2, … , rm}’, d = {d1, d2, … , dn},
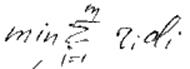
min rd; r’; ri↔rj
rd – r’d = ridi + rjdj – rjdi – ridj = (di – dj)(ri – rj)<=0, т.к. min rd
Пусть к k-му шагу размещено g эл-ов.
Тогда F(p) = F(g) + u’(p) + v(p)
F(g) – СДС между размещенными эл-ами
u’(p) – СДС между размещенными и не размещенными эл-ами
v(p) – СДС между неразмещенными эл-ами
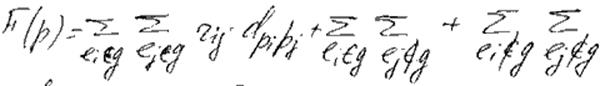
Пример:
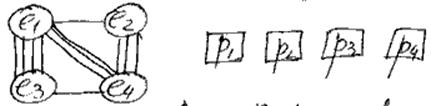
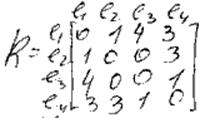
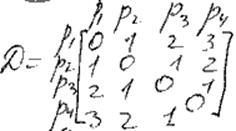
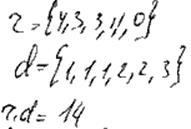
Улучшить нельзя. Не учитывает структуры графа.
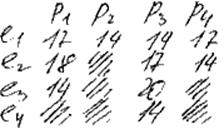
1. l1→p1, F(g) = 0, F(p) = 0+13 +4 = 17
r1 = {4,3,1}, d1 = {1,2,3}, r1d1 = 13, w(p) = 13,
r = {3,1,0}, d = {1,1,2}, rd = 4, v(p) = 4
2. l1→p2, F(p) = 0+9 +5 = 14
r1 = {4,3,1}, d2 = {1,1,2}, r1d2 = 4+3+2=9,
r = {3,1,0}, d = {1,2,3}, rd = 3+2+0=5
для l1 p2~p3, p1~p4
3. l2→p1, F(g) = r12+d21 = 1
r1 = {4,3}, d2 = {1,2}, r1d2 = 4+6=10,
r2 = {3,6}, d1 = {2,3}, r2d1 = 6+0=6
r = {1}, d = {1}, rd = 1
4. l2→p3, F(g) = r12d23 = 1, F(p) = 1+13+3 = 17
r1 = {4,3}, d2 = {1,2}, r1d2 = 4+6=10,
r2 = {3,0}, d3 = {1,2}, r2d3 = 3+0=3
r = {1}, d = {3}, rd = 3
5. l2→p4, F(g) = r12d24 = 2, F(p) = 2+10+2 = 14
r1 = {4,3}, d2 = {1,1}, r1d2 = 4+3=7,
r2 = {3,0}, d4 = {1,3}, r2d4 = 3+0=3
r = {1}, d = {2}, rd = 2
6. l3→p1, F(g) = r12d24 + r13d21 + r23d41= 1*2+4*1+0=6, F(p) = 6+8 = 14
r1 = {3}, d2 = {1}, r1d2 = 3,
r2 = {3}, d4 = {1}, r2d4 =3
r3 = {1}, d1 = {2}, r3d1= 2
7. l3→p3, F(g) = r12d24 + r13d21 + r23d41= 1*2+4*1+0=6, F(p) = 6+14 = 20
r3 = {1}, d1 = {2}, r3d1 = 2,
r1 = {3}, d2 = {1}, r1d2 =3
r2 = {3}, d4 = {3}, r2d4= 9
Замечание:
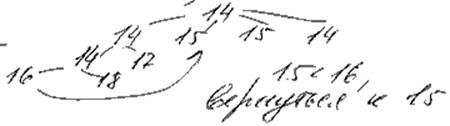
2. Конструктивные алгоритмы начального размещения
Пошаговый алгоритм.
На каждом шаге один эл-т обретает позицию
Задачи на каждом шаге:
1) выбор элемента;
2) выбор позиции для него
Пусть к k-му шагу размещены элементы множества Ek; для каждого
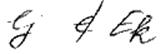
считаем
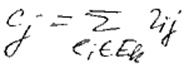
(число связей его с размещенными)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.