Теорема Понтрягина-Куратовского. Матричное представление графа. Основные задачи теории графов

Каждый граф обладает св-вами, кот. оцениваются хар-ческими числами:

1)Цикломатическое число V(G) - число ребер, кот. необх. удалить из графа, чтобы он стал деревом (или лесом, если граф был несвязным)

k=|U| - число ребер графа

|T| = n-1 - число ребер дерева

V(G) = k-n+1

V(G)=k-n+p (если дерево)

2) Хроматическое число K(G)- наим. число непересекающихся подмн-в вершин, на кот. можно разбить вершины графа так, чтобы ребра графа соединял вершины только разных подмножеств (только разноокрашенные вершины). Граф наз. плоским, если он расположен на плоским, если он расположен на плоскости так, что ребра имеют общие точки лишь в вершинах. Граф, изоморфный плоскому, но имеющий пересечения ребер, наз. планарным.

Непланарный граф нельзя нарисовать на плоскости без пересечений. Планарность - св-во, плоскость - его реализация.

Операция расширения графа - замена одного ребра Uij на 2: Uip и Uij с введением вершины р. Операция сжатия - обратная.

Исходный, расширенный и сжатый граф изоморфен с точ. до вершины 2-ой степени.

Два графа наз. гомеоморфными, если после их сжатия/расширения они становятся изоморфными. Граф, гомеоморфный плоскому также называют плоским.

Теорема Понтрягина-Куратовского:

граф планарен тогда и только тогда, когда он не содержит подграфов гомеоморфных полному графу K5 и полному графу К3,3.

3)Минимальное кол-во ребер, кот. необходимо удалить из графа, чтобы он стал планарным - число планарности Ө(G). Для полного графа: Ө (Kn)=(n-3)(n-4)/2. Гипотеза теории графов: любой планарный граф можно раскрасить <= 4-мя красками.

Граф представляется:

1) перечислением ребер

2) отображением Гхi; это мн-во верш., смежн. xi

3)отображением Гxs (расширенными Гxi) - мн-во вершин, смежн. вершинам из Xs.

Внутренне устойчивым мн-вом графов - мн-во, что любые 2 вершины в нем несмежны.

4) Число внутренней устойчивости a(G)- max кол-во несмежных вершин.

Внешне устойчивый граф - мн-во вершин Xs, выбранное т.о., что для каждой вершины

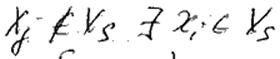
связанное с

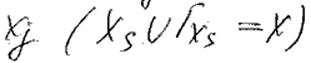
5) Число внешней устойчивости b(G) минимальная мощность Xs(b(G)=min|Xs|)

Матричное представление графа

1) Матрица инцидентности (комплексов)

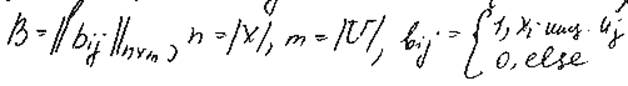
2)Матрица смежности (соединения)

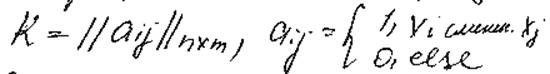
Основные задачи теории графов

1) Задачи на независимые и доминирующие мн-ва (внутр. и внешн. устойчивые мн-ва)

1. выбор проекта из n предложений . если у общ. найти наибольш. ресурс внутр. уст. мн-во (проекты кот. можно вып. одновременно)

2. размещение центров, покрывающих заданную область

3. задача о наименьшем покрытии

2) Задачи центровки.

Необх. разместить объекты так, чтобы расстояние Lij или время tij, за кот. можно добраться от центра до любого объекта, было min.

3) Задачи раскраски.

-задача на разрешение конфликтов. Например, задача размещения. Есть набор предметов, кот. нужно упаковать в ящик, при этом хрусталь и гантели, продукты и химию вместе класть нельзя. Задача осмотра. Как спланировать работу, чтобы вып-ть задачи экономично за min время.

4) Задачи центровки

Необходимо разместить объекты так, чтобы расстояния Lij или время tij, за кот. можно добраться от центра до любого объекта было min (больница, мож. охрана) - минимаксная задача. Размещение м.б. медианным. Медианой в графе наз. место, расст-ие от кот. до всех вершин минимально - минисуммная задача (расположение пункта сортировки почты)

5) Задачи на деревья

Построение всех основных деревьев графа

Построение минимального связыв. дерева

Задача Штейнера - построение дерева Штейнера. Оно отличается введением доп. вершины:

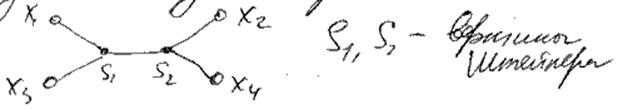
6) Кратчайшие пути

7) Нахождение Эйлерового цикла

(задача китайского почтальона) min L при прохождении по всем ветвям.

8) Задача комивояжера

min L (t, ст-ть) при прохождении всех пунктов

9) Задача "потоки в сетях" - определение max потоков между двумя вершинами

10) Транспортная задача

Есть n производителей изделия с производ-тел. ai. Есть m потребителей этого изделия с потребностями bj. Ст-ть перевозки одного изделия от i производителя к j потребителю - Cij. Необходимо составить план перевозок Х со след. ограничениями

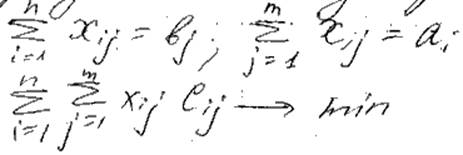
Алгоритмы автоматизированного проектирования

Осн. требования к алгоритмам АП:

1) Высокая алгоритмическая надежность - гарантир. получение прав. рез-та при любом числ. значениях исходных данных в заданном диапазоне варьирования

2) Возможность формализации. Это требование ограничивает исп-ие методов, зависимых от искусства вычислителя.

3) Малые вычислительные затраты при реализации (время, память)

4) Разумное соотношение точность/время

5) Алгоритмическая совместимость - согласованность и достат-ть вх и вых данных разных алгоритмов, работающих в одной системе.

Концепция теории алгоритмов была представлена в матем. терминах в 1930х Тьюрингом. Классы задач: 1) кот. можно решить с пом. алгоритма; 2) нерешаемые с пом. алгоритма задачи.