Отсечение произвольным окном
(выпуклым)
Y
X
Отсечение параметрически заданного отрезка прямоугольным регулярным окном (Частный случай нерегулярного)
Параметрическое описание отрезка P1(x1,y1), P2(x2,y2): P(t) = P1 + (P2 – P1)*t 0 t 1 (1) x(t) = x1 + (x2 – x1)*t 0 t 1 (2) y(t) = y1 + (y2 – y1)*t 0 t 1 t = (P(t) – P1)/(P2 – P1) Для левой: t = (x(л) – x1)/(x2 – x1) 0 t 1 Для правой: t = (x(п) – x1)/(x2 – x1) 0 t 1 Для нижней: t = (y(н) – y1)/(y2 – y1) 0 t 1 Для верхней: t = (y(в) – y1)/(y2 – y1) 0 t 1, где x(л), x(п), y(н), y(в) –координаты левой, правой, нижней и верхней сторон окна.
Пример:
Y
(1, 1)
(-1, 1)

P2(3/2, 1/2)
P2’
X
(0, 0)
P1’
P1(-3/2, -3/4)
(1, -1)
(-1, -1)
Пересечения: С левой стороной: t = (xл-x1)/x2-x1) = (-1-(-3/2))/(3/2-(-3/2)) = 1/6 С правой стороной: t = (xп-x1)/x2-x1) = (1-(-3/2))/(3/2-(-3/2)) = 5/6 С нижней стороной: t = (yн-y1)/y2-y1) = (-1-(-3/4))/(1/2-(-3/4)) = -1/5 -1/5 < 0, поэтому отвергается С верхней стороной: t = (yн-y1)/y2-y1) = (1-(-3/4))/(1/2-(-3/4)) = 7/5 7/5 > 1, поэтому отвергается. Видимый отрезок заключен в интервале 0 t 1. При t = 1/6 из уравнения (2): x(1/6) = -3/2 +[3/2 – (-3/2)](1/6) = -1 y(1/6) = -3/4 +[1/2 – (-3/4)](1/6) = -13/24 При t = 5/6 из уравнения (2): [x(5/6) y(5/6)] = [-3/2 –3/4] + [3/2 – (-3/2) 1/2 - (-3/4)](5/6) = [1 7/24]
Алгоритм Кируса-Бека
Y
b
b
R
b
a
nв
nн
0
b
X
R – выпуклая отсекающая область, nв - nн -
Внутренняя нормаль n в произвольной точке a, лежащей на границе R, удовлетворяет условию n ba 0, где b – любая другая точка на границе R. Скалярное произведение V1 и V2 = |V1| |V2| cos , где - меньший из двух углов, образованных V1 и V2. V1 V2 Если = /2, то cos = 0 и V1 V2 = 0, т.е., когда скалярное произведение двух векторов = 0, они перпендикулярны. Угол между nв и любым вектором ba всегда принадлежит интервалу -/2 …. +/2, cos > 0. Угол между внешней нормалью nн и любым вектором ba = = - , а cos( - ) = - cos < 0.
Y
b(4,4)
b
4
a
nв
nн
2
0
4
8
X
nв = i – единичный вектор вдоль оси x nн = -i
В точке 4, 4: ba = 4i + 2j nв ba = i (4i + 2j) = 4
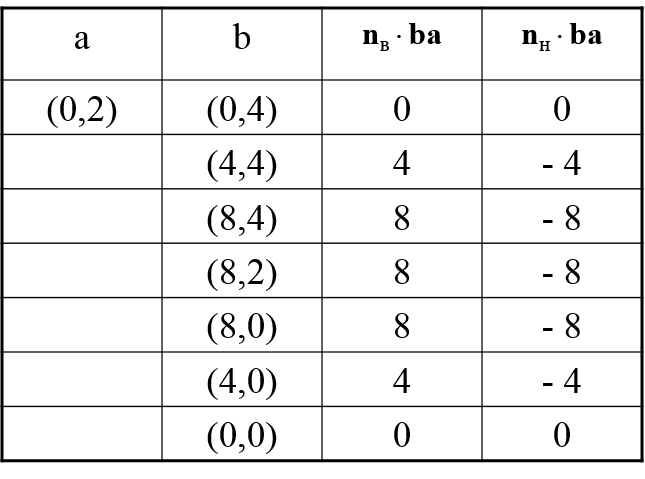
P(t) = P1 + (P2 – P1)*t 0 t 1 f – граничная точка выпуклой области R n – внутренняя нормаль к одной из ограничивающих эту область плоскостей P(t)_f – вектор из точки f в точку на отрезке P1P2 Тогда для любой точки отрезка (т.е. для любого конкретного значения t) из условия n [P(t)_f] < 0 следует, что …..
P2
f
n
P1
n [P(t)_f] < 0
из условия n [P(t)_f] = 0 следует, что …
P2
f
n
n [P(t)_f] = 0
P1
n [P(t)_f] < 0
из условия n [P(t)_f] > 0 следует, что …
P2
f
n [P(t)_f] > 0
n
n [P(t)_f] = 0
P1
n [P(t)_f] < 0
Пример.
Y
P2(9,3)
4
X
P1(-1,1)
8
P(t) = P1 + (P2 – P1)*t = [-1 1] + [10 2]t = = (10t -1)i +(2t + 10)j 0 t 1 Где i и j - единичные векторы, ориентированные вдоль осей x и y Внутренние нормали к сторонам окна: nл = i, nп = -i, nн = j, nв = -j Возьмем точку f(0,0) на левой стороне окна: P(t)_f = (10t -1)i +(2t + 10)j Уравнение nл [P(t)_f] = 10t -1 =0 Получаем t = 1/10 для пересечения отрезка с левой стороной окна Подстановка P(1/10) = [-1 1] + [10 2](1/10)= [0 1.2]
Возьмем точку f(8,4) на правой стороне окна: P(t)_f = (10t -9)i +(2t - 3)j Уравнение nп [P(t)_f] = 10t -9 =0 Получаем t = 9/10 для пересечения отрезка с правой стороной окна Подстановка P(9/10) = [-1 1] + [10 2](9/10)= [8 9.8] Возьмем точку f(0,0) на нижней стороне окна: Уравнение nн [P(t)_f] = 2t + 1 = 0 Получаем t = - 1/2 для пересечения отрезка с нижней стороной окна Это значение лежит вне интервала 0 -1, поэтому отвергается.
Возьмем точку f(8,4) на верхней стороне окна: Уравнение nв [P(t)_f] = - (2t -3) = 0 Получаем t = 3/2 для пересечения отрезка с верхней стороной окна Это значение лежит вне интервала 0 - 1, поэтому отвергается. Результат: Видимый участок отрезка P1,P2 лежим в интервале 1/10 t 9/10 или от точки [0 1.2] до точки [8 2.8]
Пример для полностью видимого отрезка.
Y
4
P2(7,3)
X
P1(1,1)
8
Для отрезка P1(1,1), P2(7,3): P(t) = [1, 1] + [6, 2]t

X
3/2
4
7/6
- 1/6
Y
8
- 1/2
X
4/3
4
- 2
- 5
Y
8
- 1/3
Внутренне и внешнее отсечение
Окно экрана
Окно 1
Окно 2
Окно 3
Приоритеты окон – в порядке убывания. Изображение в окне экрана отсекается его собственной внутренней областью и внешними областями 1, 2 и 3. Внешним отсечением можно воспользоваться при работе с вогнутым окном.
Y
P2
V3
V2
P’2
P’’2
P’1
V4
V5
P1
V6
V1
X
V1V2V3V4V5V6V1
V3V5V4V1
V1V2V3V5V6V1
Вогнутый многоугольник можно преобразовать в выпуклый. Отрезок отсекается полученным МУ с помощью алгоритма Кируса-Бека. Затем полученный МУ внешне отсекается МУ V3V5V4V3, что и дает искомый результат – P’1 P”2.
Определение факта выпуклости окна
Вершины МУ нумеруются против часовой стрелки. Для каждой i-ой вершины окно переносится так, чтобы эта вершина совпала с началом координат.
Окно поворачивается относительно начала координат так, чтобы (i+1)-ой вершина оказалась на положительной полуоси X. Вычислить знак ординаты Y (i+2)-ой вершины. Если знаки ординат всех этих вершин совпадают – окно выпуклое, иначе – невыпуклое.
V3
V4
V4
V2
V3
+
V1
V1
V2
Рис. 1
Рис. 2
Рис. 2
V1
+
V1
V4
V2
+
V3
V3
V4
V2
Рис. 4
Рис. 3
V3
V2
+
V1
V4
Рис. 5
Разрезание невыпуклого окна
(алгоритм давался на лекции)!
V5
V5
V4
V3
V4
+
V2
V3
V1
V1
V2
Рис. 1
Рис. 2
V1
V5
+
V4
V5
V3
V2
V3
V1
V4
V2
Рис. 3
Рис. 4
V1
V4
V2
+
+
V2
V3
V3
V5
V1
V4
V5
Рис. 5
Рис. 6
V1
V5
V3
V2
точка пересечения
V4
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.