Основные понятия теории графов. Изолированная и висячая вершина. Основные задачи теории графов. Проблемы надежности, страница 5

Пусть было внесено S ошибок, в процессе тестирования было обнаружено n собственных ошибок и v внесенных. Тогда

Миллс предлагает во время всего периода тестирования отмечать на графике число найденных ошибок и прогноз N.

Вторая часть модели связанна с проверкой гипотезы об N. Пусть в программе не более К собственных ошибок, количество внесенных S. Программа тестируется до тех пор пока не будут найдены все внесенные ошибки, при этом фиксируются и собственные ошибки.

При этом уровень значимости: 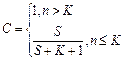  С – уровень доверия модели.

С – вероятность того, что модель будет правильно отклонять ложные предположения об N.

Например, пусть К=0, внесем S=4 ошибок, все их v=4 нашли, ни одной собственной не обнаружили. Тогда С=0.8. Чтобы С=0,95 надо внести S=19 ошибок.

Если утверждаем, что в программе не более К=3 ошибок и внеся S=6 ошибок, нашли все и не более исходных, то С=0,6.

Недостаток: нужно много тестировать

Слабое место модели: внесенные ошибки должны быть типичными для программ.

Было разработано несколько моделей, основанных на более слабых предположениях.

Простая интуитивная модель

Две группы, независимые друг от друга, тестируют одну и ту же программу своими наборами, фиксируя найденные ошибки.

После этого результаты сравниваются

N-всего ошибок.

Ni – найдено i-ой группой.

 Эффективность тестирования

Предполагают, что вероятность обнаружения для всех ошибок одинакова.

Если первая группа обнаружила N1 из всех ошибок, то то же количество было бы и для любого другого подмножества N (аппроксимация подмножества на все множество)

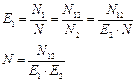
Цель любого тестирования – найти ошибки. Программу не должен тестировать автор.

Структурная надежность систем

Результирующая надежность системы при заданной ее структуре и известных значениях надежности всех ее структурных частей.

Надежность при последовательном создании частей системы.

pn – вероятность безотказной работы

 если λ_i =const следовательно

тогда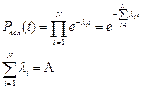

Λ – интенсивность отказов системы

т. е. экспоненциальный закон надежности для системы сохраняется если он справедлив для всех ее частей.

 среднее время безотказной работы системы.

Надежность при параллельном соединении частей системы. .

При параллельном соединении частей системы экспоненциальный закон надежности не действует.

Резервирование

Это способ повышения надежности путем включения элементов, способных выполнять функции основных элементов в случае их отказа. Различают общее, раздельное и смешанное резервирование:

Ø  Общее – резервируется все изделие.

Ø  Раздельное – резервирование отдельных частей

Ø  Смешанное – резервирование «узких мест» и всего в целом.

Различают постоянное резервирование и резервирование замещением.

Ø  Постоянное – резервные элементы включены вместе с остальными и работают в одном режиме.

Ø  Замещением – резервные элементы замещают основные после их отказа.

При резервировании замещением по режиму работы различают нагруженный, ненагруженный и облегченный резерв.

§  При нагруженном резерве резервная аппаратура работает в том же режиме, что и основная. Используется там где потеря данных недопустима.

§  Облегченный резерв – резервная аппаратура включена в сеть, но ничего не делает. В момент отказа заново решает задачу.

§  Ненагруженный – аппаратура резерва в сеть не включена, при отказе тратится время на включение и загрузку.

Мажоритарное резервирование.

Берется нечетное количество элементов и на выходе берется значение наибольшего количества сигналов.

Ррез=Рм(р³ +3р² (1-р))=РмР²(3-2р)

Имеет смысл, ели рЮ0,5. Надежность мажоритарного механизма играет главную роль.

Метода расчета надежности

Различаются из-за знаний об элементах, режимах работы, условиях работы. Пусть сбой одного элемента приводит к отказу системы, отказы элементов события случайные и независимые.

Различают притирочный, ориентировочный и общий расчеты надежности.