А(о) — амплитудная частотная характеристика;
«о) — фазовая частотная характеристика.
Выражение (13) называется комплексно-частотной функцией звена или системы. При изменении частоты от О до +ф конец вектора W00) очертит в комплексной плоскости кривую, называемую амплитудно-фазовой характеристикой (АФХ). Один из возможных видов АФХ, соответствующей уравнению (14), изображен на рисунке 1.
Прологарифмируем выражение (14):
201g = 20 ща) ![]() . (15) 23
. (15) 23
В выражении (15) множитель 20 введён для перевода амплитуды в децибелы (дб).
График зависимости Цо) 201gA(o) от lg о называется логарифмической амплитудно-частотной характеристикой звена или системы (ЛАЧХ).
График зависимости ф(о) от lg о называется логарифмической фазочастотной характеристикой (ЛФЧХ).
На рисунке 2 в качестве примера приведены ЛАЧХ и ЛФЧХ системы.


Рис. 2. Логарифмическая амплитудная Цо) и фазовая ![]() характеристики
системы
характеристики
системы
2.2. Элементы аналогового моделирования автоматических систем
Один из эффективных способов анализа и синтеза автоматических систем является электронное моделирование, основанное на тождественности уравнений, описывающих натуру и модель.
Электронная модель автоматической системы состоит из звеньев, соответствующих динамйческим звеньям моделируемой системы.
Модели динамических звеньев создаются на основе операционных усилителей и пассивных электрических элементов, которые включаются в прямую цепь и цепь обратной связи операционного усилителя таким образом, как это показано на рис. За, Использование операционного усилителя дает возможность реализовать требуемые зависимости между входными и выходными воздействиями с большой точностью .
Рисунок 36, на котором показана структурная схема динамического звена, позволяет получить основные соотношения, характеризующие рассматриваемое звено:
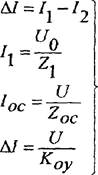
6

Рис. З. Схема включения (а) и структурная схема (б) модели динамического звена на основе операционного усилителя
Совместное решение уравнений ( 16) дает выражение
![]()
коу zoc 4
При условии стремления коэффициента усиления операционного усилителя к бесконечности Коу -» оо уравнение (17) упрощется и принимает вид:
![]()
Переходя к операторной форме, можно получить передаточную функцию, соответствующую уравнению ( 1 9),
![]()
Из выражения (19) следует, что при составлении схемы моделируемого звена достаточно установить такие пассивные цепи на входе оперишонного усилителя и в цепи обратной связи, чтобы отношение их полных сопротивлений Ир) и Zl(p) совпало с передаточной функцией.
На рисунке 4 приведены принципиальные схемы моделей динамических звеньев, исследуемых в настоящей лабораторной работе.
В качестве примера получим передаточную функцию, схема которой приведена на рисунке 46,
U(p) ас (р) _ рС2 (20)
Uo(p) 4(р) pC2Rl
Или, переходя к оригиналу, получим
U(1) =![]()
где Т = RlC2 — постоянная времени.
Таким образом, данная схема моделирует интегрирующее звено. Аналогичным образом можно определить назначение остальных схем рисунка 4.
![]()
7
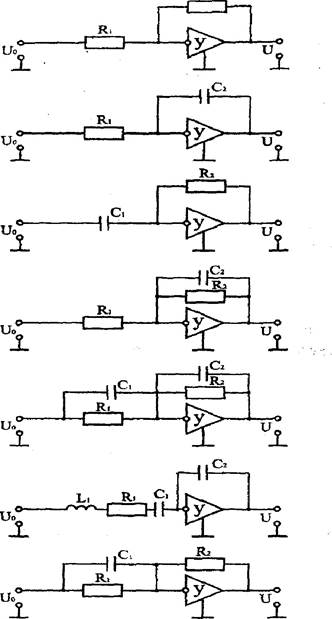
Рис. 4. Принципиальные схемы динамических звеньев
Электронные модели могут быть построены с использованием двух принципов: с периодизацией (повторением) решения и без периодизации,
![]()
![]()
![]() В моделях без периодизации решения исследование, как
правило, проводится в реальном масштабе времени. Реальное время переходного
процесса в автоматической системе составляет от долей секунды до десятка
секунд, поэтому для ее экспериментального исследования требуются приборы,
работающие в инфранизком диапазоне частот.
В моделях без периодизации решения исследование, как
правило, проводится в реальном масштабе времени. Реальное время переходного
процесса в автоматической системе составляет от долей секунды до десятка
секунд, поэтому для ее экспериментального исследования требуются приборы,
работающие в инфранизком диапазоне частот.
![]() Периодизация
решения осуществляется за счет приведения исследуемой системы в исходное
состояние и подачи входных воздействий с частотой, лежащей в области звуковых
частот, что позволяет использовать при исследовании стандартных доступных
приборов.
Периодизация
решения осуществляется за счет приведения исследуемой системы в исходное
состояние и подачи входных воздействий с частотой, лежащей в области звуковых
частот, что позволяет использовать при исследовании стандартных доступных
приборов.
Переход из области низких частог в область более высоких с масштабом т, требует уменьшения постоянных времени исследуемой системы также в т раз.
Настоящая модель работает в искусственном (ускоренном) масштабе времени, равном 100.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.