Остальные
величины: ![]() –
безразмерная температура поверхности заготовки;
–
безразмерная температура поверхности заготовки; ![]() –
безразмерная температура поверхности заготовки на выходе из кристаллизатора;
–
безразмерная температура поверхности заготовки на выходе из кристаллизатора; ![]() –
безразмерная температура поверхности заготовки в конце зоны вторичного
охлаждения;
–
безразмерная температура поверхности заготовки в конце зоны вторичного
охлаждения; ![]() –
толщина корки стали на выходе из кристаллизатора.
–
толщина корки стали на выходе из кристаллизатора.
При расчете
температуры поверхности ![]() исходим
из уравнения (3.39). Определяем на основании значений температуры поверхности
на выходе из кристаллизатора
исходим
из уравнения (3.39). Определяем на основании значений температуры поверхности
на выходе из кристаллизатора ![]() и
в конце зоны вторичного охлаждения
и
в конце зоны вторичного охлаждения ![]() параметр
параметр
![]() ;
затем рассчитываем значение
;
затем рассчитываем значение ![]() по
уравнению (3.40) и в заключение по уравнению (3.38) находим температуру
по
уравнению (3.40) и в заключение по уравнению (3.38) находим температуру ![]() .
.
Пример 3.5 Рассчитать температуру на
поверхности широкой грани листовой заготовки толщиной 210 ![]() на
расстоянии 3
на
расстоянии 3 ![]() от
уровня стали в кристаллизаторе, если высота стали в нем равна 650
от
уровня стали в кристаллизаторе, если высота стали в нем равна 650 ![]() ,
скорость разливки
,
скорость разливки ![]() ,
температура затвердевания стали
,
температура затвердевания стали ![]() °С,
температура поверхности заготовки при выходе из кристаллизатора 1000 °С, а в
конце вторичного охлаждения 800 °С.
°С,
температура поверхности заготовки при выходе из кристаллизатора 1000 °С, а в
конце вторичного охлаждения 800 °С.
1. Определим по
параболическому соотношению приблизительную толщину застывшей корки ![]() на
выходе из кристаллизатора:
на
выходе из кристаллизатора:
![]()
![]() ;
;
![]() .
.
2. Рассчитаем безразмерную температуру поверхности заготовки на выходе из кристаллизатора и на конце зоны вторичного охлаждения:
![]()
![]() .
.
3. Рассчитаем параметр ![]() :
:
![]()
![]() .
.
4. Определим ![]() :
:
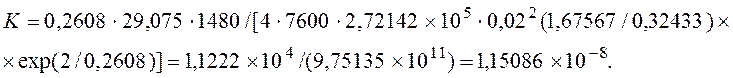
5. Рассчитаем ![]() :
:
![]() ;
;
![]()
![]() .
.
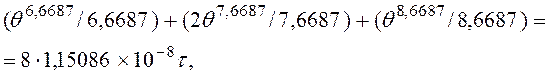
![]() –
время, за которое исследуемая часть заготовки достигает глубины 3
–
время, за которое исследуемая часть заготовки достигает глубины 3 ![]() .
Так как скорость отливки
.
Так как скорость отливки ![]() ,
,
![]() .
.
Уравнение
преобразуем, приведя к общему знаменателю и подставив значение ![]() ,
получим:
,
получим:
![]()
Итерационным методом получаем
значение ![]() .
По уравнению (3.38 а)
.
По уравнению (3.38 а) ![]()
![]()
![]()
Температура поверхности 905 °С.
3.2.5 Возможности определения коэффициента теплоотдачи
при непрерывной разливке стали
Коэффициент теплоотдачи в кристаллизаторе
Обозначим верхнюю
зону сравнительно плотного контакта образующей корки заготовки со стенкой
кристаллизатора индексом I, а нижнюю зону кристаллизатора, где возникает зазор
между заготовкой и кристаллизатором, индексом II. На основании общеизвестной теории отведения тепла А.И.
Вейника можно рассчитать время ![]() ,
за которое отводится тепло перегрева стали над температурой ликвидуса по отношению
,
за которое отводится тепло перегрева стали над температурой ликвидуса по отношению
![]() (3.41)
(3.41)
где ![]() –
релятивная толщина
–
релятивная толщина ![]() слитка;
слитка;
![]() –
коэффициент теплоотдачи в кристаллизаторе;
–
коэффициент теплоотдачи в кристаллизаторе;
![]() –
температура разливаемой стали;
–
температура разливаемой стали;
![]() –
температура охлаждающей воды.
–
температура охлаждающей воды.
Подставим ![]() ,
где
,
где ![]() –
длина зоны 1 кристаллизатора, а
–
длина зоны 1 кристаллизатора, а ![]() –
скорость разливки, и получим соотношение для длины зоны 1:
–
скорость разливки, и получим соотношение для длины зоны 1:
![]() (3.42)
(3.42)
Предположим, что
для отношения (3.42) выполнено условие: длина ![]() отвечает
длине зоны, в которой отводится тепло перегрева. Это представление значительно
упрощено, однако уравнение дает приблизительно основание для расчета длины
отвечает
длине зоны, в которой отводится тепло перегрева. Это представление значительно
упрощено, однако уравнение дает приблизительно основание для расчета длины ![]() ,
которая позволяет рассчитать тепловой поток от поверхности отливки,
согласующийся с экспериментально замеренными значениями.
,
которая позволяет рассчитать тепловой поток от поверхности отливки,
согласующийся с экспериментально замеренными значениями.
Пример 3.6 Определить длину зоны
кристаллизатора ![]() ,
в которой сталь находится в прямом контакте со стенкой кристаллизатора, при непрерывной
разливке слитков размером 300
,
в которой сталь находится в прямом контакте со стенкой кристаллизатора, при непрерывной
разливке слитков размером 300 ![]() 300
300
![]() .
Температура разливки
.
Температура разливки ![]() °С,
температура затвердевания
°С,
температура затвердевания ![]() °С,
скорости разливки
°С,
скорости разливки ![]() .
Релятивная толщина
.
Релятивная толщина ![]() .
Подставляемые физические величины:
.
Подставляемые физические величины: ![]() ;
;
![]() ,
,
![]() .
.
![]() .
.
Таким образом, длина зоны ![]() .
.
А.А. Скворцов и А.Д. Акименко вводят для полного коэффициента теплоотдачи в верхней зоне кристаллизатора уравнение
![]() (3.43)
(3.43)
где ![]() –
коэффициент теплоотдачи от поверхности заготовки к кристаллизатору;
–
коэффициент теплоотдачи от поверхности заготовки к кристаллизатору;
![]() –
толщина стенки кристаллизатора;
–
толщина стенки кристаллизатора;
![]() –
коэффициент теплоотдачи между охлаждающей водой и кристаллизатором.
–
коэффициент теплоотдачи между охлаждающей водой и кристаллизатором.
Коэффициент ![]() можно
теоретически определить на основании критериального уравнения для конвективного
переноса тепла:
можно
теоретически определить на основании критериального уравнения для конвективного
переноса тепла:
![]() (3.44)
(3.44)
которое действительно для ![]() ;
эти условия будут всегда выполнены при разливке из промежуточного ковша в
кристаллизатор (число Рейнольдса колеблется от
;
эти условия будут всегда выполнены при разливке из промежуточного ковша в
кристаллизатор (число Рейнольдса колеблется от ![]() до
до
![]() ).
Рассчитанные значения из уравнения (3.44) примерно на 60% выше полученных
экспериментально. Причиной несогласования являются факторы, которые не учтены
критериальным уравнением, прежде всего неровности поверхности заготовки и наличие
смазки изложницы.
).
Рассчитанные значения из уравнения (3.44) примерно на 60% выше полученных
экспериментально. Причиной несогласования являются факторы, которые не учтены
критериальным уравнением, прежде всего неровности поверхности заготовки и наличие
смазки изложницы.
Для зоны II определение общего коэффициента теплоотдачи от поверхности заготовки через медную стенку кристаллизатора к охлаждающей воде возможно по уравнению (3.45) [17]
![]() (3.45)
(3.45)
которое не учитывает излучения при
передаче тепла с поверхности заготовки к кристаллизатору. Эта предпосылка для
зоны 2 действительна, если зазор между кристаллизатором и заготовкой < 0,02 ![]() .
.
Значение коэффициента
![]() ,
можем рассчитать с помощью критериального уравнения
,
можем рассчитать с помощью критериального уравнения
![]() (3.46)
(3.46)
Коэффициент
теплоотдачи ![]() ,
который включает влияние излучения:
,
который включает влияние излучения:
![]() (3.47)
(3.47)
В соотношение (3.47)
включено излучение тепла зазором между поверхностью заготовки и стенкой
кристаллизатора. Величина ![]() определяется
так же, как и при стационарной разливке заготовки
определяется
так же, как и при стационарной разливке заготовки
![]() (3.47 а)
(3.47 а)
где ![]() –
теплопроводность вещества в зазоре;
–
теплопроводность вещества в зазоре;
![]() – зазор;
– зазор;
![]() –
температура внутренней поверхности кристаллизатора, °С,
К.
–
температура внутренней поверхности кристаллизатора, °С,
К.
Зазор ![]() можно
определить из балансного соотношения. Тепло, прошедшее с поверхности слитка
через зазор, отводится медной стенкой кристаллизатора к воде.
можно
определить из балансного соотношения. Тепло, прошедшее с поверхности слитка
через зазор, отводится медной стенкой кристаллизатора к воде.
Подведенное тепло ![]()
Отведенное тепло ![]()
![]() (3.48)
(3.48)
Так как ![]() ,
другим членом уравнения можно пренебречь.
,
другим членом уравнения можно пренебречь.
Температура внутренней поверхности кристаллизатора определяется
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.