Составление статистической таблицы и проведение группировок и сводок по имеющимся данным для анализа структуры рынка периодических изданий, страница 3

Объем	Кол-во	Среднее значение цены
560	1	130
600	6	97
650	6	117
680	3	128
700	5	157
720	4	178
750	9	199
760	6	239
780	5	269
800	6	331
820	3	380
850	2	395
860	3	423
900	6	457
950	5	497
1000	5	551
1200	4	716
1400	1	1400
Итого:	80

Вывод: Цена не зависит от объема аккумулятора.

ü группировка по количеству цветов

Вывод: С возрастанием количества цветов в телефоне, цена увеличивается в основной массе телефонов.

4.  Комбинационная группировка:

ü группировка по количеству цветов дисплея и цене

Количество цветов\Цена	88-270,4	270,4-452,8	452,8-635,2	635,2-817,6	817,6-1000	Итого:
4096	14	0	0	0	0	14
65000	16	7	2	1	0	26
65536	9	5	5	1	0	20
65546	0	1	0	0	0	1
262000	3	5	4	0	2	14
262144	1	2	2	0	0	5
Итого:	43	20	13	2	2	80

Обобщающие статистические показатели

ü Рассчитаем эти показатели в зависимости от параметра «Цена»

Графическое представление дискретного ряда распределения – полигон

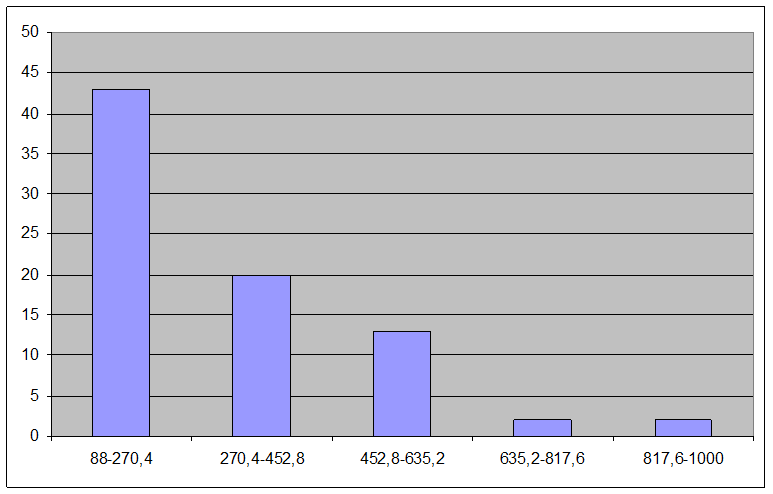
Гистограмма.

Наибольшей плотностью распределения обладает интервал 88-270,4 у.е.

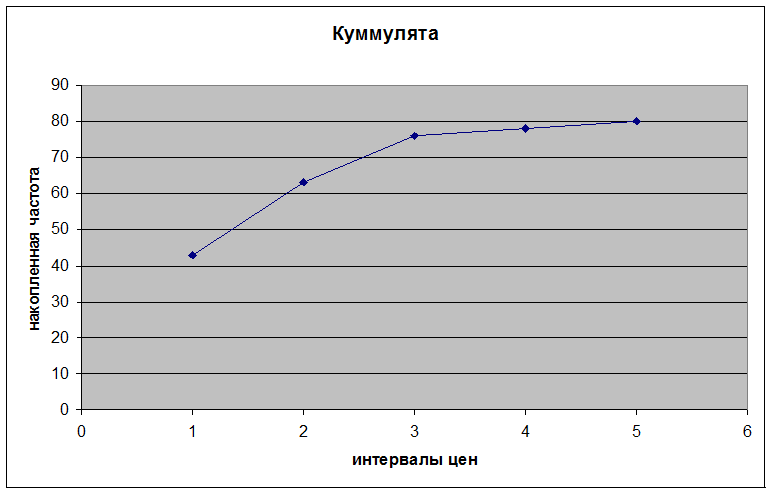
Куммулята.

1.  Среднее арифметическое (взвешенное):

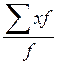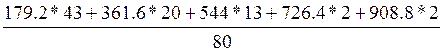===316

Средняя цена телефонов представленных на рынке 316 у.е.

2.  Мода:

Модальный интервал 88-270,4, так как наибольшее количество элементов равно 43 и соответствует этому интервалу .

Mo(x) = x₀ + ΔMo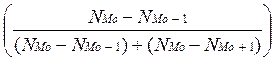=206,8364

Наиболее часто встречающаяся цена телефона равна  206,8364 у.е.

3.Медиана:

Медианный интервал равен 88-270,4

Me(x) = x₀ + ΔMe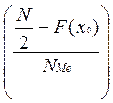=88+182,4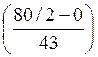=257,6744

Средняя цена телефона из интервала 88-270,4 равна 257,6744 у.е.

Так как Среднее ≠ Моде ≠ Медиане (316≠ 206,8≠ 257,7), то ряд распределения – асимметричен.

4. Размах вариации:

R = X_max – X_min = 1000-88= 912 (у.е.)

Амплитуда колебаний значений признака (цены) составляет 912 у.е.

5. Дисперсия:

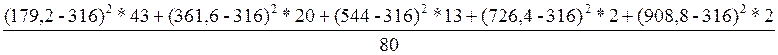== =7407,72

Среднее из квадратов отклонения от средней величины составляет 7407,72

5.  Средне-квадратическое отклонение:

σ_x ===86,06811

В среднем, цена телефона отклоняется от среднего значения на 86,06811 у.е.

7. Коэффициент вариации:

υ = ·100%=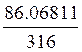=27,23674%

ü Рассчитаем те же показатели в зависимости от параметра «Вес»

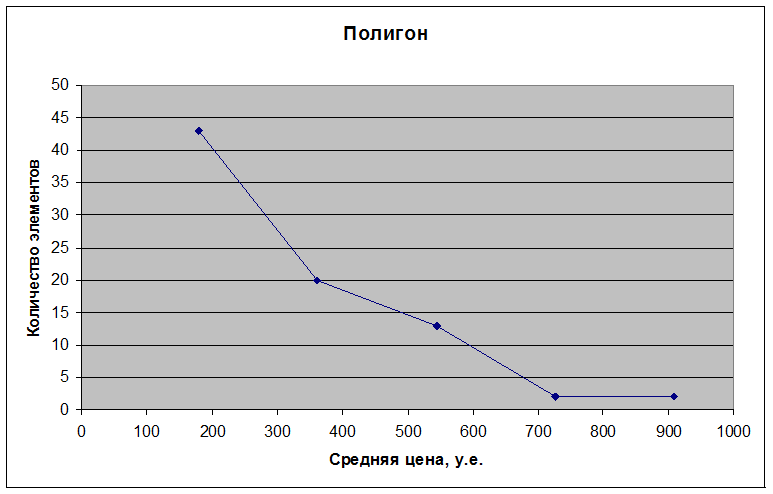
Полигон.

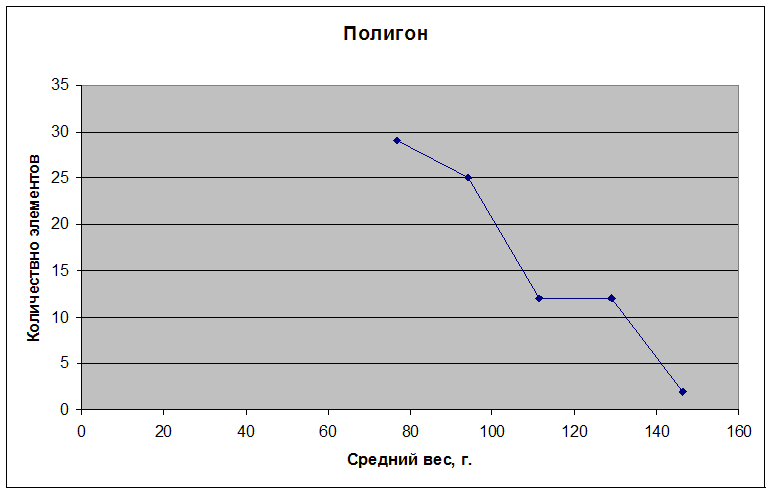
Гистограмма распределения числа мобильных телефонов в наблюдении в зависимости от их веса.

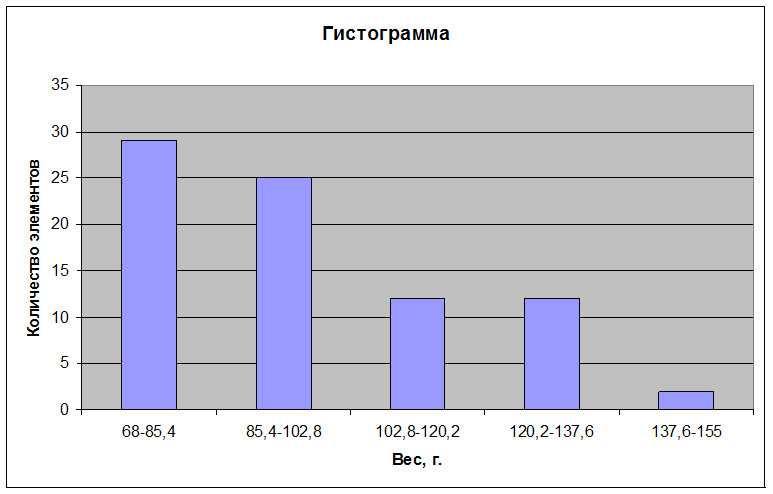
Куммулята.

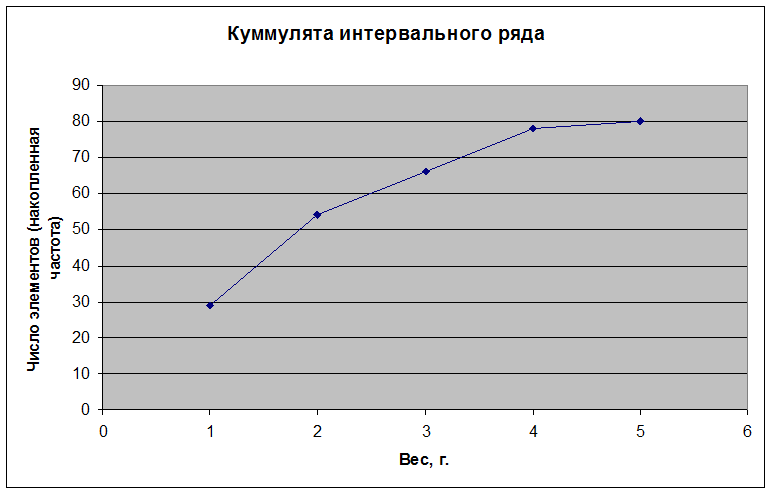
1.  Среднее арифметическое (взвешенное):

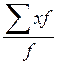== 96,9275

3.  Мода:

Модальный интервал 68-85,4, так как наибольшее количество элементов равно 29 и соответствует этому интервалу .

Mo(x) = 83,29091

Наиболее часто встречающийся вес телефона равен  83,29091 г.

3.Медиана:

Медианный интервал равен 68-85,4

Me(x) =60,344

Средняя цена телефона из интервала 68-85,44 равна 60,344 г.

Так как Среднее ≠ Моде ≠ Медиане (96,93≠ 83,29≠ 60,344), то ряд распределения – асимметричен.

4. Размах вариации:

R = X_max – X_min = 155-68= 87 (г.)

Амплитуда колебаний значений признака (цены) составляет 912 г.

5. Дисперсия:

=51,11735977

Среднее из квадратов отклонения от средней величины составляет 51,12

6.  Средне-квадратическое отклонение:

σ_x == 7,149641

7. Коэффициент вариации:

υ = ·100%=7,37%