Составление статистической таблицы и проведение группировок и сводок по имеющимся данным для анализа структуры рынка журналов и газет, страница 3

4.  Комбинационная группировка

Равноинтервальная комбинационная группировка по цене и объему

		Цена,руб.					итого
№	Объем, стр.	5,00-85,6	85,6-166,2	166,2-246,8	246,8-327,4	327,4-408
1	4-75,2	29	8	0	0	0	37
2	75,2-146,4	14	7	1	2	0	24
3	146,4-217,6	10	3	1	0	1	15
4	217,6-288,8	1	2	0	0	0	3
5	288,8-360	0	1	0	0	0	1
	Итого	54	21	2	2	1	80

Вывод: так как наибольшие значения в таблице не расположены ни на одной из её диагоналей, то линейной зависимости между объемом журнала и ценой  нет.

Обобщающие статистические показатели

№	Цена	Ср. интервал цены	% к итогу	Кол-во элементов	Накопленная частота
1	5-85,6	45,3	68,75	55	55
2	85,6-166,2	125,9	22,5	18	73
3	166,2-246,8	206,5	5	4	77
4	246,8-327,4	287,1	2,5	2	79
5	327,4-408	367,7	1,25	1	80
	Итого		100	80

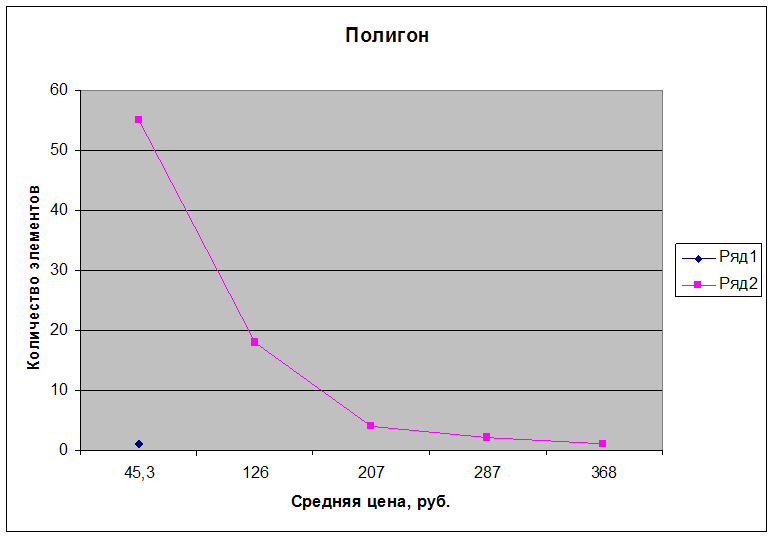
Наибольшей плотностью распределения обладает интервал 45,3-126

1.  Среднее арифметическое (взвешенное):

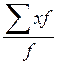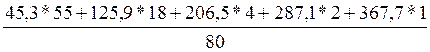== = 81,57

Вывод: Средняя цена по всей совокупности газет и журналов равна 81,57 рублей

2.  Мода:

Модальный интервал 5-85,6, так как наибольшее количество элементов равно 55 и соответствует этому интервалу .

Mo(x) = x₀ + ΔMo=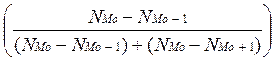

=5 + 80,6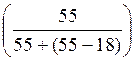= 53,18478261

Вывод: наиболее часто встречающаяся цена журнала равна  53,18478261 рубля

3.  Медиана:

Медианный интервал равен 5-85,8

Me(x) = x₀ + ΔMe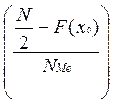=5 + 80,6 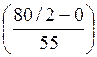=63,33

Вывод: Средняя цена журнала из интервала 5-85,6 равна 63,33 рубля

Так как Среднее ≠ Моде ≠ Медиане (81,57 ≠ 53,2 ≠ 63,33), то ряд распределения – асимметричен.

4. Размах вариации:

R = X_max – X_min = 408-5= 403 (руб.)

Вывод: амплитуда колебаний значений признака (цены) составляет 403 руб.

5. Дисперсия:

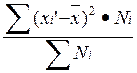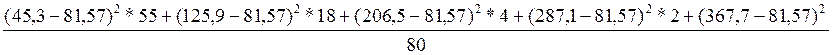 = = = 4206,3931

Вывод: среднее из квадратов отклонения от средней величины составляет 4206,3931

6. Средне-квадратичное отклонение:

σ_x = = = 64,85671207

Вывод: в среднем, цена журнала отклоняется от среднего значения на 64,85671207 руб.

7. Коэффициент вариации:

υ = ·100% = 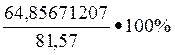= 79,51049659%

Вывод:

№	Объем, стр	Ср.интервал объема	Кол-во элементов	% к итогу	Накопленная частота
1	4-75,2	39,6	37	46,25	37
2	75,2-146,4	110,8	24	30	61
3	146,4-217,6	182	15	18,75	76
4	217,6-288,8	253,2	3	3,75	79
5	288,8-360	324,4	1	1,25	80
	Итог		80	100

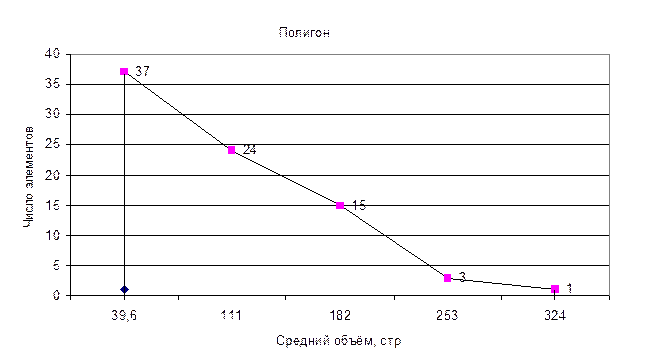
Плотность распределения элементов примерно одинакова на всех интервалах

1.  Среднее арифметическое (взвешенное):

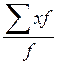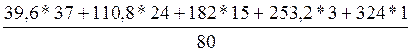== = 99,23

Вывод: Средний объем по всей совокупности газет и журналов равен 99,23 страниц.

2.  Мода:

Модальный интервал 75,2, так как наибольшее количество элементов равно 37 и соответствует этому интервалу .

Mo(x) = x₀ + ΔMo=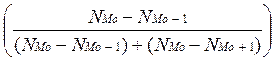

=4 + 71,2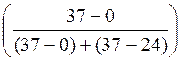= 56,668

Вывод: наиболее часто встречающийся объем журнала равен  56,688 страниц.

3.  Медиана:

Медианный интервал равен 75,2-146,4

Me(x) = x₀ + ΔMe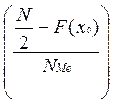=75,2 +  71,2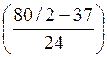=84,10

Вывод: 50% журналов имеют объем до 84,1 страниц, а еще 50% свыше 84,1 страницы.

Так как Среднее ≠ Моде ≠ Медиане (99,23 ≠ 56,688 ≠ 84,10), то ряд распределения – асимметричен.

4. Размах вариации:

R = X_max – X_min = 360-4= 356 (стр.)

Вывод: амплитуда колебаний значений признака (объема) составляет 356 страниц.

5. Дисперсия:

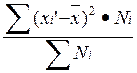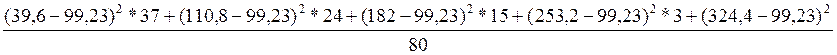 = = = 4492

Вывод: среднее из квадратов отклонения от средней величины составляет 4492 страницы

6. Средне-квадратичное отклонение:

σ_x = = = 67,02

Вывод: в среднем, объем журнала отклоняется от среднего значения на 67,02 страницы

7. Коэффициент вариации:

υ = ·100% = 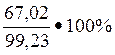= 67,54%

Вывод: