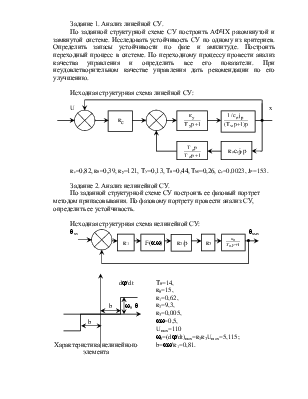







Задание 1. Анализ линейной СУ.
По заданной структурной схеме СУ построить АФЧХ разомкнутой и замкнутой системе. Исследовать устойчивость СУ по одному из критериев. Определить запасы устойчивости по фазе и амплитуде. Построить переходный процесс в системе. По переходному процессу провести анализ качества управления и определить все его показатели. При неудовлетворительном качестве управления дать рекомендации по его улучшению.
Исходная структурная схема линейной СУ:






 U x
U x
![]()
![]()
![]()
![]()




![]()
![]()
![]()
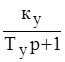



![]()
![]()
![]()
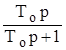 косеjрр кс=0,82,
к0=0,39, ку=121, ТУ=0,13, Т0=0,44,
ТМ=0,26, се=0,0023, JP=153.
косеjрр кс=0,82,
к0=0,39, ку=121, ТУ=0,13, Т0=0,44,
ТМ=0,26, се=0,0023, JP=153.
Задание 2. Анализ нелинейной СУ.
По заданной структурной схеме СУ построить ее фазовый портрет методом припасовывания. По фазовому портрету провести анализ СУ, определить ее устойчивость.
Исходная структурная схема нелинейной СУ:


![]()

![]()



![]()
![]()
![]()
![]()
![]() qвх
qвых
qвх
qвых
![]()
![]()

 к1 F(aw) к2/р к3
к1 F(aw) к2/р к3
![]()
 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
dj/dt
b w0 q
b
![]()
Характеристика нелинейного элемента
Т0=14, к0=15, к1=0,62, к2=9,3, к3=0,005,
aw=0,5,
Umax=110
w0=(dj/dt)max=к2к3Umax=5,115;
b=aw/к1=0,81.
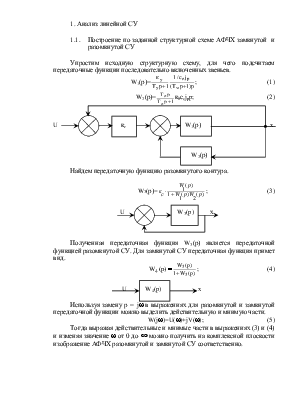
1. Анализ линейной СУ
1.1. Построение по заданной структурной схеме АФЧХ замкнутой и разомкнутой СУ
Упростим исходную структурную схему, для чего подсчитаем передаточные функции последовательно включенных звеньев.
W1(р)=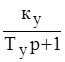
 ;
(1)
;
(1)
W2(р)=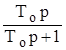 к0сеjpp;
(2)
к0сеjpp;
(2)
 |
|||||
 |
|||||


![]()
![]()
![]()
![]()




![]()
![]() U
кc W1(р)
x
U
кc W1(р)
x

![]()
![]() W2(р)
W2(р)
Найдем передаточную функцию разомкнутого контура.
W3(р)=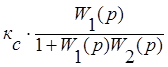 ;
(3)
;
(3)
![]()
![]()
![]()
![]()

![]()
![]()
U W3(p) х
Полученная передаточная функция W3(р) является передаточной функцией разомкнутой СУ. Для замкнутой СУ передаточная функция примет вид.
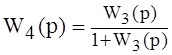 ; (4)
; (4)

U W4(p) x
Используя замену р = jw в выражениях для разомкнутой и замкнутой передаточной функции можно выделить действительную и мнимую части.
W(jw)=U(w)+jV(w); (5)
Тогда
выражая действительные и мнимые части в выражениях (3) и (4) и изменяя значение
w от 0 до ![]() можно получить на комплексной
плоскости изображение АФЧХ разомкнутой и замкнутой СУ соответственно.
можно получить на комплексной
плоскости изображение АФЧХ разомкнутой и замкнутой СУ соответственно.
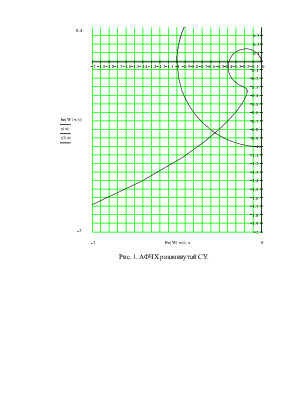
Построение таблиц значений и графиков производим на ЭВМ с помощью Mathcad.
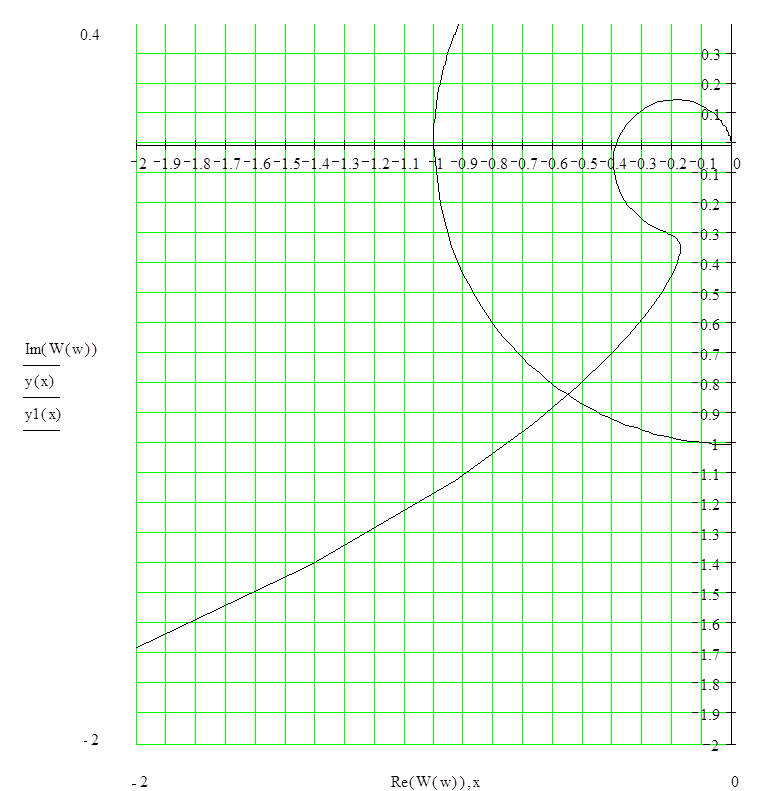 |
Рис. 1. АФЧХ разомкнутой СУ.
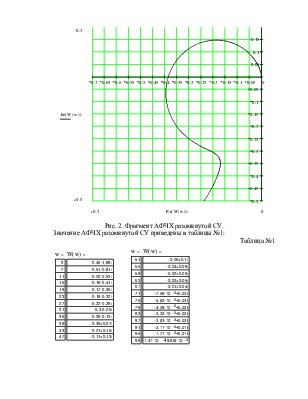
 |
Рис. 2. Фрагмент АФЧХ разомкнутой СУ.
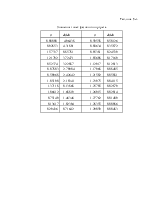
Значение АФЧХ разомкнутой СУ приведены в таблицы №1:
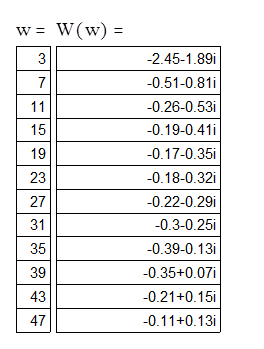 |
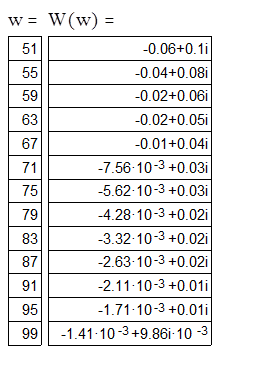 |
||

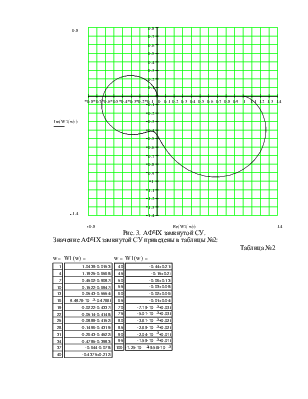
Рис. 3. АФЧХ замкнутой СУ.
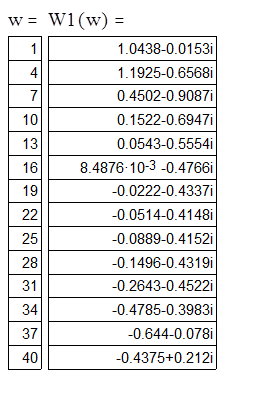
Значение АФЧХ замкнутой СУ приведены в таблицы №2:
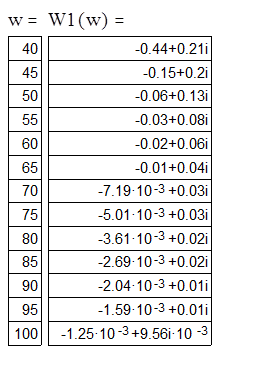 |
1.2. Исследование устойчивости СУ по из критериев. Определение запасов устойчивости по фазе и амплитуде
Определим устойчивость СУ по критерию Гурвица.
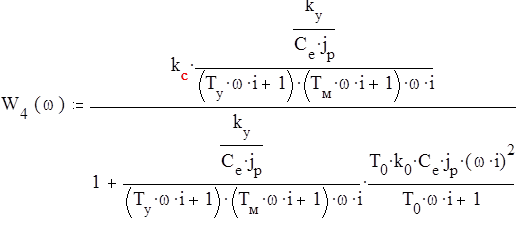 |
Упрощая данное выражение, получим:
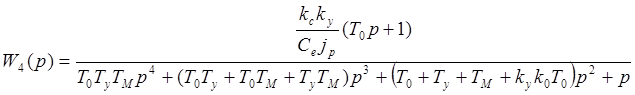 ;
;
Тогда характеристическое уравнение имеет вид:
![]() ; (6)
; (6)
Подставим исходные данные в уравнение (6) и разделим его на р:
![]() ; (7)
; (7)
Так как а0 = 0,0149 > 0, а1 = 0,2054 > 0, а2 = 21,5936 > 0, а3 = 1 > 0, то система может быть устойчивой (необходимое условие устойчивости).
Составим определители Гурвица:
D1 = а1 > 0;
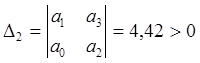 ;
;
D3 = а3D2 > 0;
Все определители Гурвица положительны, следовательно система управления устойчива.
Запасы устойчивости по амплитуде h и фазе y определим из графика АФЧХ разомкнутой системы. Построим единичную окружность. h определяется расстоянием от точки пересечения графиком АФЧХ действительной оси до точки с координатами (-1, i0 ). y определяется углом между прямой и отрицательной действительной полуосью. Прямая проходит через начало координат и точку пересечения АФЧХ с единичной окружностью.
По рис. 1 видно, что запасы устойчивости по фазе и амплитуде соответственно равны:
- запас устойчивости по амплитуде h = 0.616;
- запас устойчивости по фазе y = 56°.
1.3.Построение переходного процесса в СУ.
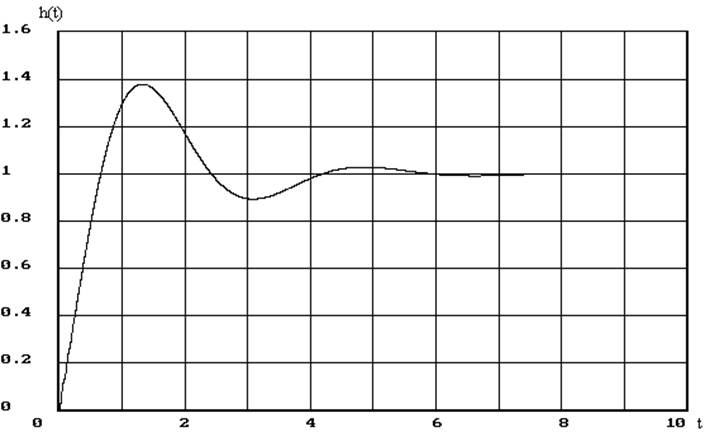 |
Рис.4. График переходного процесса в СУ.
Значения h(t) приведены в таблице №3.
Таблица №3
|
t |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,2 |
1,35 |
|
h(t) |
0 |
0,3 |
0,63 |
0,91 |
1,14 |
1,29 |
1,33 |
1,38 |
|
t |
1,4 |
1,6 |
1,8 |
2 |
2,5 |
3 |
3,5 |
4 |
|
h(t) |
1,37 |
1,34 |
1,26 |
1,18 |
0,99 |
0,9 |
0,92 |
0,98 |
|
t |
4,5 |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
10 |
|
h(t) |
1,02 |
1,03 |
1,01 |
1 |
0,99 |
0,99 |
1 |
1 |
1.4. Анализ качества управления СУ
По полученному графику переходного процесса определяем следующие показатели качества управления СУ:
1. Установившееся значение hуст = 1.
2. Время регулирования tp = 3,6с.
3. Перерегулирование s = (hmax-hуст)/hуст*100% = 38%.
4. Декремент затухания c = 15,2.
5. Время достижения первого максимума tmax = 1,35 c.
6. Время нарастания tн = 0,7с.
7. Число колебаний n = 1.
8. Период колебаний Т = 3,45с.
9. Частота колебаний w = 0,29.
С учетом всего вышесказанного можно сделать вывод, что качество управления СУ хорошее и дополнительной коррекции не требует.
2. Анализ нелинейной СУ
2.1. Построение по заданной структурной схеме СУ ее фазового портрета
Рассчитываем значения b = 0,81 и w0 = 5,115 для трехпозиционного реле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.