Проектирование синхронных счетчиков. Сигналы, поступающие на вход счетчика. Асинхронный двоичный счетчик

приведены карты Карно для функций возбуждения счетчика на D–триггерах, а в табл. 8 для счетчика на JK–триггерах.

Таблица 6                      

Таблица 7                      

Из таблиц 4 и 5 видно, что в десятичном счетчике в коде 2421 из 16 возможных состояний используются только 10. Остальные шесть являются запрещенными, они никогда не появляются при правильной работе счетчика. Это Q₃Q₁; Q₃Q₂Q₁; Q₄Q₁; Q₃Q₂; Q₄ и Q₄Q₂. На этих наборах аргументов значения функций можно выбирать произвольно. Отметим на картах Карно эти состояния крестиком (x). Как следует из таблицы входов JK–триггера, клетки, отмеченные на картах Карно символом “–”, также можно заполнять 0 или 1 по усмотрению разработчика. При этом минимизация функций возбуждения сводится к минимизации не полностью определенных логических функций (при получении дизъюнктивных форм объединять в контуры можно 1, –, х, при получении конъюнктивных форм объединяются 0, –, х).

Таблица 8                      

Из карт Карно получаем:

Для счетчика на D–триггерах

D₁ = , 

D₂ = , 

D₃ = , 

D₄ = .

Для счетчика на JK–триггерах

J₁ = K₁ = 1,

J₂ = ,     K₂ = Q1,

J₃ = Q₂Q₁,              K₃ = ,

J₄ = Q₃,                  K₄ = Q₃Q₂Q₁.

3. Организация переноса

В каждом десятичном разряде при переходе из состояния 9 в состояние 0 (в рассматриваемом примере из состояния S₁₅  в состояние S₀) необходимо вырабатывать сигнал переноса в следующий разряд.

Схему, формирующую сигнал переноса для счетчиков на JK–триггерах, изменяющих свое состояние по срезу счетного импульса, можно построить, используя выражение 

Сout_i = Cout_{i –1}K₁₅, где Cout_{i –1} – сигнал переноса из предыдущего разряда;

K₁₅ = Q₄Q₃Q₂Q₁ – конституента единицы, соответствующая десятичной цифре 9. (Для данного примера 9 соответствует 15. См. табл. 4 и табл. 5).

Конституента единицы не всегда отвечает минимальному выражению, необходимому для образования сигнала переноса. В десятичных счетчиках всегда имеются запрещенные состояния, учет которых позволяет получить минимальное выражение для сигнала переноса. Для этого необходимо занести на карту Карно запрещенные состояния (х) и  конституенту единицы (1) того набора, который соответствует десятичной цифре 9 в данном двоично–десятичном коде. Остальные клетки диаграммы заполняются нулями (табл. 9). Объединив клетки, выделенные полужирным шрифтом, получим минимальное выражение, необходимое для организации сигнала переноса.

В нашем случае

Сout_i = Cout_{i –1}Q₃Q₂Q₁

и, следовательно, сигнал переноса можно сформировать с помощью элемента И, на входы которого подаются сигналы    Cout_{i –1},Q₃,Q₂,Q₁.

Таблица 9                                          

Для счетчика на D–триггерах рассуждения относительно сигнала переноса в следующий разряд похожи на предыдущие, но эти триггеры срабатывают по фронту счетного сигнала, а потому перенос формируется на основе выражения

Сout_i = Cout_{i –1}K₀, гдеK₀ = – конституента единицы, соответствующая десятичной цифре 0. (Для данного примера 0 соответствует 0. См. табл. 4 и табл. 5).

Поэтому перенос здесь вырабатывается элементом И, на входы которого подаются сигналы   Cout_{i –1},.

 исключено в соответствии с табл. 10.

Таблица 10                                        

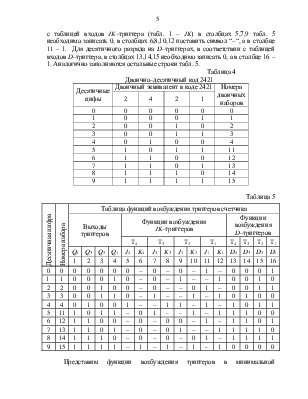
Однако при такой реализации переноса возможно появление ложных сигналов из–за риска сбоя (см. рис. 4,а).

На рисунке приведена схема переноса из группы, состоящей из одного D–триггера. Здесь комбинационная схема представлена двумя элементами И, на выходах которых реализуются уравнения:  Задержка переключения триггера в данном случае приводит к появлению статических рисков сбоя в обоих случаях при переходе с набора 01 на набор 10. Устранить эти сбои можно, выполнив комбинационную схему на элементах ИЛИ (рис. 4,б).

Из временных диаграмм видно, что в данной схеме риски сбоя не появляются. Выходные сигналы С1 и С2 при необходимости можно изменить инвертированием.

В счетчике на JK-триггерах, срабатывающих по срезу импульса на тактовом входе, риска сбоя нет (рис. 4,в).

Таким образом, перенос в счетчиках на D–триггерах лучше сделать на элементе ИЛИ, реализующем выражение

Cout_i = Cout_{i –1}.

4. Примеры схем и временных диаграмм

Схема двоично–десятичного счетчика, построенная на JK–триггерах приведена на рис. 5. Временные диаграммы (без учета задержек элементов) этого счетчика показаны на рис. 6.

На рис. 7 приведена схема двоично–десятичного счетчика, построенная на D–триггерах. Временные диаграммы этого счетчика показаны на рис. 8.

5. Создание дешифратора

При создании дешифратора для полученного счетчика необходимо учесть, что в счетчике используются не все возможные состояния. Это позволит упростить схему дешифратора. Для рассматриваемого примера из табл. 10, полученной по табл. 6, видно, что каждое рабочее состояние имеет хотя бы одно соседнее