














Если это не удается, то каждую группу строим по синхронному методу, а группы включаем последовательно (пример, счетчик с K = 25)
3. Первая тактовая группа строится по асинхронному методу, т.е. в этой группе триггеры соединяются последовательно, образуя счетчик с коэффициентом K = 2m, где m – число разрядов в группе.
4. для тактируемой группы синтез осуществляется по синхронному методу, при этом совмещённая таблица функций возбуждения заполняется только по строкам, соответствующим срезу выходного импульса тактовой группы (переходу 1/0), а в остальных строках ставится прочерк.
Пример. Построить асинхронный делитель на 6.
Определяем число разрядов счетчика
n = ]log26[ = 3.
1. Разряды счетчика разбиваем на две группы: 1-й разряд будет формировать тактовые импульсы для 2-го и 3-го разрядов.
2. Заполняем совмещённую таблицу (табл. 10).
3. заполняем карты Карно (табл. 11) и определяем функции возбуждения:
J1 = K1 = K2 = K3 = 1,
J2 = Q3’,
J3 = Q2,
по которым строим счётчик.
Таблица 10
совмещённая таблица счетчика с K = 6
|
Q3Q2Q1 |
J3K3 |
J2 K2 |
J1 K1 |
|
000 |
- - |
- - |
1 - |
|
* 001 |
0 - |
1- |
- 1 |
|
010 |
- - |
- - |
1 - |
|
* 011 |
1- |
- 1 |
- 1 |
|
100 |
- - |
- - |
1 - |
|
* 101 |
- 1 |
0 - |
- 1 |
В табл. 10 символом * отмечены состояния, при переходе из которых образуется перепад 1/0 (срез импульса на выходе первого разряда).
Таблица 11
|
Счетчик с K =6 на JK–триггерах |
||||||||||||||
|
J1 |
K1 |
|||||||||||||
|
Q2Q1 Q3 |
00 |
01 |
11 |
10 |
Q2Q1 Q3 |
00 |
01 |
11 |
10 |
|||||
|
0 |
1 |
- |
- |
1 |
0 |
- |
1 |
1 |
- |
|||||
|
1 |
1 |
- |
х |
х |
1 |
- |
1 |
х |
х |
|||||
|
J2 |
K2 |
|||||||||||||
|
Q2Q1 Q3 |
00 |
01 |
11 |
10 |
Q2Q1 Q3 |
00 |
01 |
11 |
10 |
|||||
|
0 |
- |
1 |
- |
- |
0 |
- |
- |
1 |
- |
|||||
|
1 |
- |
0 |
х |
х |
1 |
- |
- |
х |
х |
|||||
|
J3 |
K3 |
|||||||||||||
|
Q2Q1 Q3 |
00 |
01 |
11 |
10 |
Q2Q1 Q3 |
00 |
01 |
11 |
10 |
|||||
|
0 |
- |
0 |
1 |
- |
0 |
- |
- |
- |
- |
|||||
|
1 |
- |
- |
х |
х |
1 |
- |
1 |
х |
х |
|||||
Рисунок 6. Асинхронный делитель на 6
Счётчики, реализованные с использованием управляющих входов, не застрахованы от появления ложных выходных наборов, но это никогда не приводит к сбою в работе счётчиков.
Синхронные счётчики указанного класса позволяют реализовать импульсные последовательности с высокой точностью привязки фронтов.
Если высокая степень точности привязки импульсной последовательности не требуется, то предпочтительнее асинхронная реализация счётчиков.
Как синхронные, так и асинхронные счётчики с использованием управляющих входов максимально защищены от сбоев по установочным входам.
Задание.
Построить синхронные и асинхронные делители частоты с использованием управляющих входов на JK- и D -триггерах:
1) K = 12,
2) K = 14,
3) K = 24,
4) K = 25.
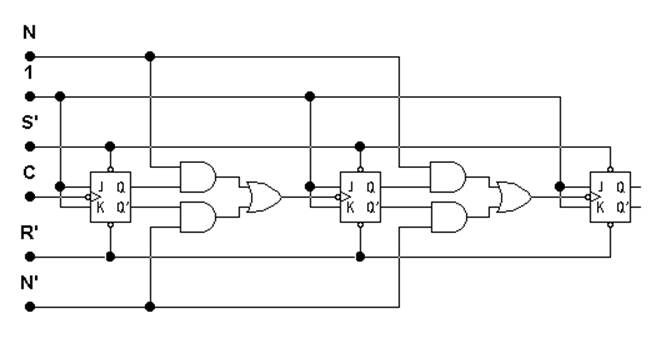 |
Рисунок 7. Асинхронный реверсивный счётчик
Изменение направления счёта в PC происходит в зависимости от значения сигнала N: при N = 1 счётчик считает в прямом направлении, при N = 0 - в обратном.
Асинхронный РС практически не может быть использован, так как при изменении направления счёта может изменяться код, записанный в PC. Например, при переходе от суммирования к вычитанию, если предыдущий триггер находится в состоянии 1, то сигнал на входе последующего триггера изменится с 1 на 0, что приведёт к его опрокидыванию.
Этого недостатка лишены синхронные счётчики, так как они изменяют своё состояние по срезу импульса тактовой частоты, и изменение N в промежутке между двумя срезами (т.е. на протяжении периода тактовой частоты) не влияет на состояние PC. Пример синхронного двоичного PC приведен на рис. 8.
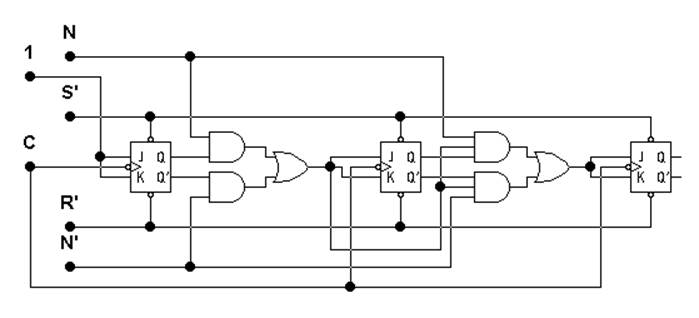
Рисунок 8. Синхронный реверсивный счётчик
Построение PC без зоны нечувствительности с произвольным K осуществляется методом синтеза счётчиков с использованием управляющих входов. Аналогично можно строить PC с зоной нечувствительности.
Построим синхронный PC без зоны нечувствительности с K = 3 на JK-триггерах.
Строим совмещённую таблицу (табл. 12) и синтезируем функции возбуждения J2, К2, J1, K1.
Таблица 12
|
Код состоян. |
N = 1 |
N = 0 |
||
|
Q2Q1 |
J2 K2 |
J1 K1 |
J2 K2 |
J1 K1 |
|
0 0 |
0 - |
1 - |
1 - |
0 - |
|
0 1 |
1 - |
- 1 |
0 - |
- 1 |
|
1 0 |
- 1 |
0 - |
- 1 |
1 - |
С помощью карт Карно (табл. 13) получаем
J2 = Q1’N’ ![]() Q1N;
Q1N;
J1 = Q2’N ![]() Q2N’.
Q2N’.
Таблица 13
|
Реверсивный счетчик с K = 3 на JK–триггерах |
||||||
|
N = 1 |
||||||
|
J1 |
K1 |
|||||
|
Q1 Q2 |
0 |
1 |
Q1 Q2 |
0 |
1 |
|
|
0 |
1 |
- |
0 |
- |
1 |
|
|
1 |
0 |
х |
1 |
- |
х |
|
|
J2 |
K2 |
|||||
|
Q1 Q2 |
0 |
1 |
Q1 Q2 |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
- |
- |
|
|
1 |
- |
х |
1 |
1 |
х |
|
|
Реверсивный счетчик с K = 3 на JK–триггерах |
||||||
|
N = 0 |
||||||
|
J1 |
K1 |
|||||
|
Q1 Q2 |
0 |
1 |
Q1 Q2 |
0 |
1 |
|
|
0 |
0 |
- |
0 |
- |
1 |
|
|
1 |
1 |
х |
1 |
- |
х |
|
|
J2 |
K2 |
|||||
|
Q1 Q2 |
0 |
1 |
Q1 Q2 |
0 |
1 |
|
|
0 |
1 |
0 |
0 |
- |
- |
|
|
1 |
- |
х |
1 |
1 |
х |
|
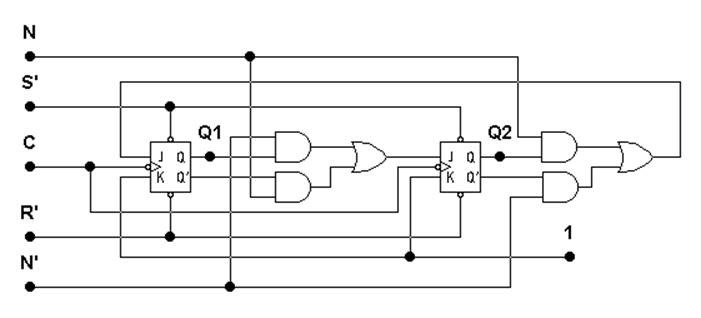 |
Схема счётчика представлена на рис. 9.
Рисунок 9. Синхронный реверсивный счётчик с K = 3
Построим синхронный PC с зоной нечувствительной на JK-триггерах. К = 3.
При R1R2 = 10 PC должен считать в прямом направлении, при R1R2 = 01 - в обратном, при R1R2 = 00 PC не изменяет своего состояния (это зона нечувствительности), ситуация R1R2 = 11 является запрещённой.
Строим совмещённую таблицу (табл. 14), карты Карно (табл. 15) и синтезируем функции возбуждения.
Таблица 14
|
Код сост. |
R1R2=10 |
R1R2 = 01 |
R1R2 = 00 |
|||
|
Q2 Q1 |
J2 K2 |
J1 K1 |
J2 K2 |
J1 K1 |
J2 K2 |
J1 K1 |
|
0 0 |
0 - |
1 - |
1- |
0 - |
0 - |
0 - |
|
0 1 |
1 - |
- 1 |
0 - |
- 1 |
0 - |
- 0 |
|
1 0 |
- 1 |
0 - |
- 1 |
1 - |
- 0 |
0 - |
Из карт Карно получаем
![]()
![]() ,
,
![]()
![]() .
.
Схема счетчика показана на рис. 10.
Задание.
Построить PC без зоны нечувствительности и с зоной нечувствительности на JK-, D - и тактируемых SR- триггерах:
1) К =10,
2) К =12,
3) К =16.
Таблица 15
Реверсивный счетчик с зоной нечувствительности
|
J1 |
K1 |
||||||||||
|
R1R2 Q2Q1 |
00 |
01 |
11 |
10 |
R1R2 Q2Q1 |
00 |
01 |
11 |
10 |
||
|
00 |
0 |
0 |
х |
1 |
00 |
- |
- |
х |
- |
||
|
01 |
- |
- |
х |
- |
01 |
0 |
1 |
х |
1 |
||
|
11 |
х |
х |
х |
х |
11 |
х |
х |
х |
х |
||
|
10 |
0 |
1 |
х |
0 |
10 |
- |
- |
х |
- |
||
|
J2 |
K2 |
||||||||||
|
R1R2 Q2Q1 |
00 |
01 |
11 |
10 |
R1R2 Q2Q1 |
00 |
01 |
11 |
10 |
||
|
00 |
0 |
1 |
х |
0 |
00 |
- |
- |
х |
- |
||
|
01 |
0 |
0 |
х |
1 |
01 |
- |
- |
х |
- |
||
|
11 |
х |
х |
х |
х |
11 |
х |
х |
х |
х |
||
|
10 |
- |
- |
х |
- |
10 |
0 |
1 |
х |
1 |
||
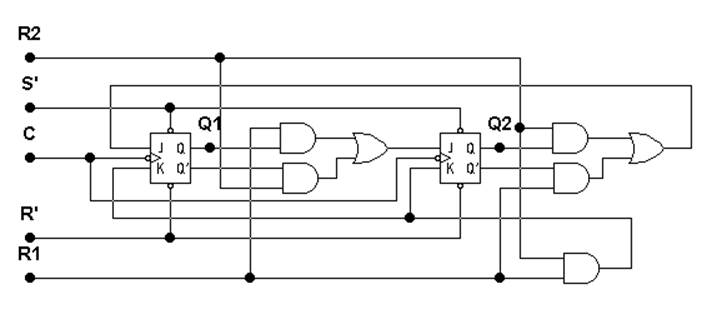 |
с зоной нечувствительности
Спроектируем устройство управления светофором с такой последовательностью смены сигналов
– красный,
– красный + желтый,
– зеленый,
– желтый,
– красный и т.д.
Для реализации выберем автомат Мура, у которого цветными индикаторами будут управлять непосредственно выходы D–триггеров.
У светофора имеются индикаторы трех цветов, поэтому в качестве элементов памяти возьмем три D–триггера. Обозначим Q0 – выход триггера, управляющего зеленым индикатором, Q1 – выход триггера, управляющего желтым индикатором, Q2 – выход триггера, управляющего красным индикатором. Примем, при Qi = 1 индикатор светится, если Qi = 0, то индикатор не светится.
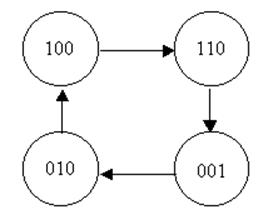
Граф переходов проектируемого автомата можно представить так, как
показано на рис. 11.
Рисунок 11
На рис. 11 обозначено
100 – красный,
110 – красный + желтый,
001 – зеленый,
010 – желтый.
Составим совмещенную таблицу переходов и входов (табл. 16)
Таблица 16
|
Q2 |
Q1 |
Q0 |
D2 |
D1 |
D0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
В левой части таблицы показаны возможные переходы автомата, в правой части – значения входных сигналов триггеров, вызывающих переход автомата в следующее состояние (при составлении таблицы учтено, что для D–триггера справедливо Qн = Dст).
Принимая D2, D1, D0 функциями Q2, Q1, Q0, составим карты Карно (табл
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.