|
Этапы |
Задачи этапа |
Модели |
|
1.Системное проектирование (этап главного конструктора) |
1. Архитектура 2. Условия работы 3. Основные ожидаемые характеристики |
Вербальные (устные) модели |
|
2. Структурное проектирование |
1. Построение структуры 2. Алгоритмы функционирования и режимы работы 3. Определение характеристик структуры:
|
1. Аналитические модели 2. Имитационные модели |
|
3. Функционально – логический этап (логическое моделирование) |
1. Разрабатываются функциональные схемы узлов и устройств 2. Анализ работоспособности:
3. Синтез средств контроля |
Модели элементов и устройств |
|
4. Проектирование электрических принципиальных схем |
Компоновка схемы с учетом:
|
Электротехнические и конструкторские модели |
|
5. Конструкторско – технологический этап |
Разработка конструкций ИС, ТЭЗ Проблемы: отвод тепла, помехи |
Графы, конструкторские модели |
|
6. Совместная отладка ПО и аппаратуры |
Оценка работоспособности |
Разработка малой машины на большой |
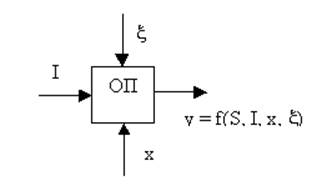 |
I – входная информация (случайная величина), х – изменяемые параметры,
x - случайные воздействия,
S – структура.
Моделирование в общем случае сводится к созданию модели объекта, подаче на нее входных воздействий и анализу реакции объекта на эти воздействия.
На сегодня нет систем сквозного проектирования СВТ с применением моделирования на всех этапах. Есть системы моделирования для этапов 2, 3, 4, 5.
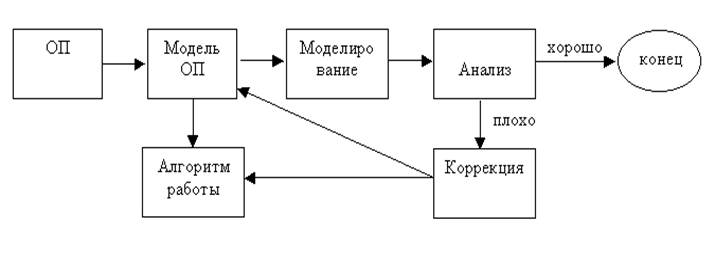 |
Модели бывают:
1. Физические.
2. Математические:
· аналитические,
· имитационные.
При построении модели объект разбивается на части. Для каждой части строится своя модель, затем из моделей частей создается модель объекта в целом.
1. Модель должна как можно точнее описывать объект проектирования.
2. Должна быть простой и наглядной.
3. Должна быть удобной для пользователя.
4. Должна иметься возможность модификации и развития модели.
5. Должны предъявляться минимальные требования к ЭВМ.
6. Надежность (защита от сбоев и т.д.).
1. Словесное описание.
2. Формализация.
3. Формула, структура для логического устройства.
4. Схема, алгоритм работы
1. Любое моделирование требует затрат (финансовых и временных).
2. Полное моделирование возможно для особо важных объектов.
Принцип 1. Модель – система логических уравнений:
· без учета времени;
· с учетом времени.
- Комбинационные схемы (КС);
- Конечные автоматы с памятью (КА) – последовательностные схемы.
Система логических уравнений решается методом итераций.
Принцип 2. Идеализация сигналов.
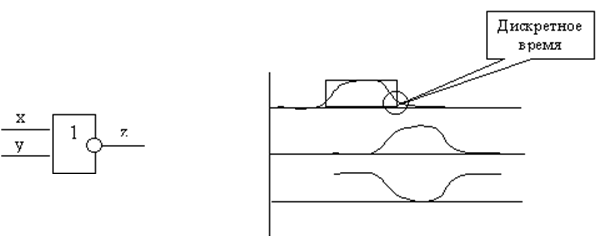 |
1. По отображению времени в моделях:
· без учета времени (синхронные методы);
· с учетом времени (асинхронные).
2. По способу представления сигналов:
· Булевские {0;1};
· Методы многозначной логики:
- при трехзначном моделировании для представления значений величин сигналов берется множество L = {0, 1/2, 1} , где 0 и 1 интерпретируются так же, как и в булевой алгебре, а 1/2 (иногда X, Н) используется для представления переходного процесса. Значение 1/2 воспринимается логическим элементом либо как 0, либо как 1, то есть если некоторый сигнал изменяет свое значение, то в течение переходного процесса значение сигнала может восприниматься как 0 или как 1, поэтому при моделировании оно обозначается как 1/2, причем это обозначение надо рассматривать как единый символ;
- четырехзначная модель (алгебра Поста): 0, переходы 01 и 10, 1;
- пятизначная модель: 0, 01, 10, 1, Х – неопределенное значение;
- восьмизначная модель: 0, 1, чисто алгоритмические переходы 01 и 10, которые обозначаются специальными символами “+” и “–” ,соответственно, статические риски сбоя S0 и S1, динамические риски сбоя D+ и D–.
Вот примеры многозначных моделей элемента И (другие примеры см. ниже):
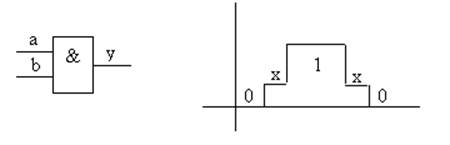 Троичная модель
Троичная модель
|
a\b |
0 |
x |
1 |
|
0 |
0 |
0 |
0 |
|
х |
0 |
х |
х |
|
1 |
0 |
х |
1 |
Троичные модели других элементов см. ниже.
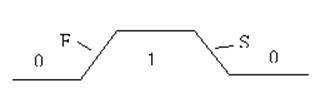 Пятизначная модель
Пятизначная модель
|
0 |
1 |
F |
S |
x |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
F |
S |
x |
|
F |
0 |
F |
F |
x |
x |
|
S |
0 |
S |
x |
S |
x |
|
x |
0 |
x |
x |
x |
x |
3. По способу решения систем уравнений:
· на каждом шаге;
· по событиям.
шаг – безразмерная единица времени; событие – любое изменение сигналов.
Одной из целей моделирования является оценка эффективности средств контроля и резервирования, которая проводится путем внесения в исследуемое устройство неисправностей и выявления способности средств контроля обнаруживать, а средств резервирования маскировать их. При этом необходимо в процессе моделирования иметь возможность изменять состав и кратность неисправностей. Поэтому нужно уметь создавать модели дискретных (цифровых) устройств с неисправностями, управляемыми в процессе моделирования.
Здесь возможны два варианта:
1. Если модели элементов создаются при подготовке к моделированию, то неисправности в них можно внести, введением специальных переменных.
2. Если модели элементов уже имеются и их изменение нежелательно, то неисправности вносятся в схему функционального узла с помощью имитаторов.
Пример: y = x1 & x2
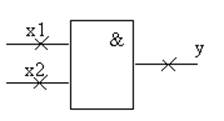 Крестиком
отмечены места возможных мест неисправностей типа константа º 0 и константа º 1.
Крестиком
отмечены места возможных мест неисправностей типа константа º 0 и константа º 1.
Для внесения неисправностей вводятся переменные:
Hi – имитатор неисправности º 0, i – нечетный индекс,
Hj – имитатор неисправности º 1, j – четный индекс.
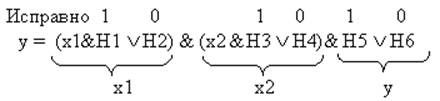 |
|
Тип неисправности |
H1 |
H2 |
H3 |
H4 |
H5 |
H6 |
y |
|
x1 º 0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
x1 º 1 |
1 |
1 |
1 |
0 |
1 |
0 |
x2 |
|
x2 º 0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
x2 º 1 |
1 |
0 |
1 |
1 |
1 |
0 |
x1 |
|
y º 0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
y º 1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
Исправно |
1 |
0 |
1 |
0 |
1 |
0 |
x1&x2 |
элемент И – имитатор º 0;
элемент ИЛИ – имитатор º 1.
U1, U2 – управляющие переменные:
U1 = 0 ® x/1 = 0, имитация неисправности º 0.
U1 = 1 ® x/1 = x1.
U2 = 1 ® x/2 = 1, имитация неисправности º 1.
U2 = 0 ® x/2 = x2.
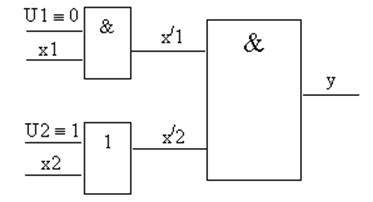 |
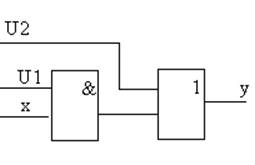
Имитация обеих неисправностей (º 0, º 1) реализуется схемой
|
U1 |
U2 |
x |
y |
|
0 |
0 |
x |
0 |
|
0 |
1 |
x |
1 |
|
1 |
0 |
x |
x |
|
1 |
1 |
x |
1 |
![]()
нормальная работа
a. {0;1} без учета задержек.
b. Модель – система уравнений.
c. Шаг итерации – однократное решение системы.
d. Такт (цикл) – многошаговый итерационный процесс, в результате которого для фиксированных входных сигналов получаются установившиеся значения внутренних и выходных сигналов.
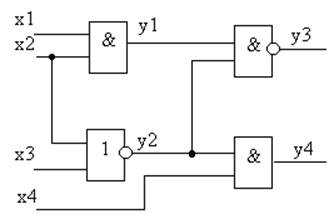 |
![]() y1 = x1· x2
y1 = x1· x2
![]() y2 = x2 Ú x3
y2 = x2 Ú x3
![]() y3 = y1 · y2
y3 = y1 · y2
y4 = y2 · x4
При реализации БСМ применяют:
1. метод простых итераций,
2. метод Зейделя,
3. метод событийного моделирования.
- составить систему уравнений,
- задать начальные значения выходам всех элементов,
- задать входной набор,
- решить систему уравнений,
- сравнить полученные значения с начальными, если совпали, то конец, иначе всем выходам элементов присвоить полученные значения как начальные и решить систему.
Для КС всегда есть решение, для КА решения может не быть.
Для остановки решения ранжируют схему (определяют ранг R).
Алгоритм ранжирования: Элементам, имеющим только внешние входы, присваивают ранг r = 0; элементам, имеющим входы, связанные с элементом с r = 0, присваивают r = 1 и т. д. R = rmax
Максимальное количество итераций P= R + 1.
- ранжирование схемы,
- составление системы уравнений в соответствии с рангами,
- решение системы уравнений.
Решение получается за одну итерацию.
Для КА приходится разрывать обратные связи.
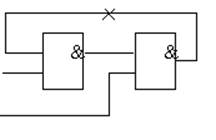 x –
место разрыва обратной связи.
x –
место разрыва обратной связи.
В процессе моделирования решаются уравнения только элементов, подозрительных на изменение их выходов. В больших схемах в каждый момент времени переключаются » 5 % элементов. И, казалось бы, на этом можно съэкономить время. Найти подозрительные на переключение элементы вроде бы просто: элемент переключится, если у него на входах произошли изменения. Однако на поиск таких элементов потребуется время, возможно даже большее, чем при моделировании по шагам.
Булевский синхронный метод позволяет:
1. Проводить анализ логики работы.
2. Выявлять неисправности.
3. Выявлять запрещенные наборы.
Недостаток: не обнаруживает гонки.
– {0;1} (как и раньше),
– шаг – (как и раньше),
– такт – (как и раньше),
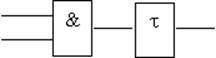 – t - учет задержек.
– t - учет задержек.
Задержка t задается в шагах, с каждым шагом из счетчика (t) вычитается 1.
Недостаток: не обнаруживает статические и динамические риски
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.