Источники питания ПК. Выпрямители и фильтры. Трансформаторы. Стабилизаторы и преобразователи напряжения

Таким образом, нам предстоит рассмотреть 12 вариантов схем:

2 (В)  х  3 (Ф)  х  2 (Н)  =  12

2.2.1. Модели типа C

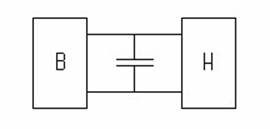
Рис. 2.8. Фильтр типа C

Это простейшая схема с одним энергозапасающим элементом - конденсатором. Цель моделирования – построение зависимости напряжения на конденсаторе (и нагрузке) от времени. В этом простейшем случае можно не ставить численный эксперимент, а для моделирования временных процессов воспользоваться готовыми теоретическими формулами.

Посмотрим, что происходит в промежутке между двумя максимумами питающего напряжения (в однополупериодной схеме расстояние между этими максимумами составляет 20 мс, в двухполупериодной – 10 мс).

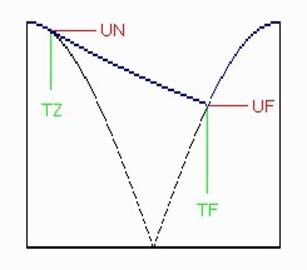
Рис. 2.9. Точки переключения и типы кривых

Очевидно, что в моменты максимумов диод (диоды) выпрямителя открыт и напряжение на конденсаторе совпадает с сетевым. Внутри рассматриваемого интервала есть два момента переключения диода: сначала диод закрывается, когда сетевое напряжение «проваливается» к нулю, а затем открывается вновь на новом подъеме сетевого напряжения. Таким образом, в начале и конце интервала, пока диод открыт, форма напряжения на конденсаторе – исходный сетевой косинус (удобно считать, что при t = 0 Uсети = Um), а при закрытом диоде в середине интервала конденсатор разряжается по экспоненциальному (с постоянной времени C*Rн) или линейному (dUc/dt = Iн / C) закону.

Итак, формы искомой зависимости известны, осталось определить моменты переключения диода – моменты переключения с одной функции на другую.

Диод закрывается, когда ток разряда конденсатора, напряжение которого следует косинусоидальному закону, сравнивается с током, потребляемым нагрузкой:

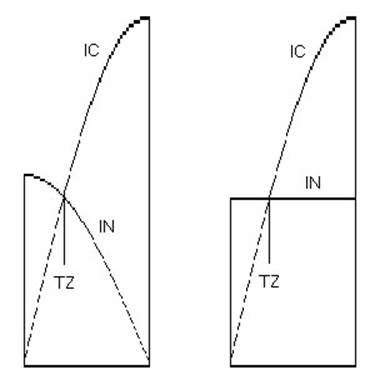
Рис. 2.10. Момент запирания диода (диодов)

Uc = Um * cos ( * t)

Ic = C * dUc/dt = C * Um *  * sin ( * t) = Iн

Iн = Uc / Rн   или    Iн = const

Эти соотношения определяют момент TZ запирания диода, их физический смысл заключается в том, что конденсатору не нужно так быстро разряжаться, чтобы обеспечить ток нагрузки.

Диод открывается вновь, когда растущее после провала напряжение сети сравнивается с уменьшающимся напряжением на разряжающемся конденсаторе:

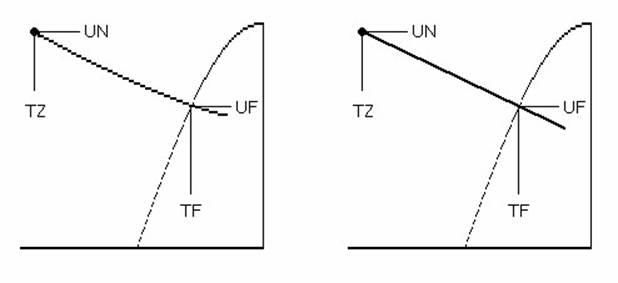
Рис. 2.11. Момент открытия диода (диодов)

Uсети = UN * exp(-(t – TZ)/(Rн*C))   или   Uсети = UN – Iн * (t – TZ) / C UN = Um * cos ( * TZ)

Эти соотношения определяют момент TF отпирания диода.

Представленный алгоритм моделирования реализует программа 02010.bas. Для решения соответствующих уравнений и поиска значений TZ и TF программа использует численный метод деления отрезка пополам.

В рассмотренном простейшем случае для определения величины пульсаций напряжения на нагрузке можно обойтись и без моделирования, приближенно оценивая амплитуду пульсаций по формуле:

Uc  Iн / C * t где t = 20 мс для однополупериодного выпрямителя, t = 10 мс – для двухполупериодного; Iн = Um / Rн для резистивной нагрузки.

2.2.2. Модели типа CRC

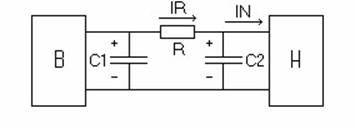
Рис. 2.12. Фильтр типа CRC

При моделировании этой схемы должна быть решена задача вывода модели на установившийся режим. Очевидно, что напряжение UC1 на первом конденсаторе в момент максимума сетевого напряжения совпадает с этим максимумом. Поэтому моделирование каждого периода целесообразно начинать именно с этого момента (при t = 0: Uсети = Um, UC1 = Um). Однако в рассматриваемой модели два основных параметра, которые необходимо отслеживать UC1 и UC2. Напряжение на втором конденсаторе в начальный момент периода  t = 0 неизвестно, и для первого из рассматриваемых периодов его приходится задавать произвольно (например, UC2 = Um). Для каждого следующего периода начальное значение UC2 равно результату моделирования UC2 в предыдущем периоде. Модель выйдет на установившийся режим, когда при моделировании очередного периода конечное значение UC2 совпадет с начальным (обозначение в программе UC2S).

Фрагмент программ 02020.bas и 02030.bas, реализующий описанную выше процедуру выхода модели на установившийся режим:

UC2 = 1: UC2S = 0: NC = 0

WHILE ABS(UC2 - UC2S) > .01

NC = NC + 1

UC2S = UC2

Моделирование очередного периода, дающее новое значение UC2

WEND

PRINT NC

Моделирование еще одного периода с выводом результатов

Производится подсчет числа NC периодов, пройденных до выхода на установившийся режим, это число выводится на экран. Признаком достижения установившегося режима считается достаточно точное совпадение начального и конечного значения UC2 в очередном периоде: ABS(UC2 - UC2S)  .01.

Теперь о построении самой модели. Совокупность ее основных параметров A определена – это UC1 и UC2. Внешним воздействием B следует считать сетевое напряжение с учетом