Равно-пролётные неразрезные балки. Приведение нагрузки к эквивалентной равномерно распределенной

        Лекция 3

Равно-пролётные неразрезные балки

         3.1. Общие сведения

Чаще всего расчётные схемы балочных сооружений, которые используются в строительстве, являются  статически неопределимыми. Для их расчета применяются специальные методы строительной механики. Расчет может быть в значительной степени облегчен за  счет  использования накопившегося справочного материала или с использованием существующих программ и соответствующем компьютерном обеспечении (например FastFraim).  Ниже мы приведем некоторые  табличные формы представления справочной информации и покажем принципы их использования на равнопролётных неразрезных балках. Нужно помнить, что принципиально таблицы и графики готовых решений можно построить только  в  том случае, когда имеется линейная зависимость между геометрическими размерами, параметрами  нагрузки  и усилиями. В них приводятся  безразмерные  параметры  усилий,  которые для получения усилий в конкретном сооружении необходимо умножать  на соответствующий размерный параметр.

          3.2. Расчёт равно-пролётных неразрезных балок 

Равно-пролетные неразрезные балки широко распространены и поэтому хорошо изучены. Имеется широкий набор таблиц по их расчету.  По  мере удаления от загруженного пролета усилия в балке затухают. Так, уже  в третьем пролете опорный момент уменьшается в 15 ‚ 20 раз, поэтому для расчета балки с любым  количеством  пролетов  практически  достаточно иметь решения для балок до пяти пролетов включительно.

При действии на балку постоянной нагрузки она (нагрузка) может быть как распределённой (например, покрытие), так и сосредоточенной (например, световые фонари на мосту), поэтому на первом этапе расчёта статически неопределимых неразрезных балок необходимо нагрузку привести к одному виду – распределённой нагрузке. В табл.2 приведены схемы замены  заданной нагрузки, приложенной к балке,  эквивалентной распределенной нагрузкой. При действии распределённой нагрузки  вычислены значения опорных моментов в двух-, трех-, четырех- и пяти-пролетных балках при загружении их равномерно -  распределенной нагрузкой. Эти данные приведены в табл. 3.

                                                                                                                           Таблица 2 

Приведение нагрузки к эквивалентной равномерно распределенной (q_эквив)

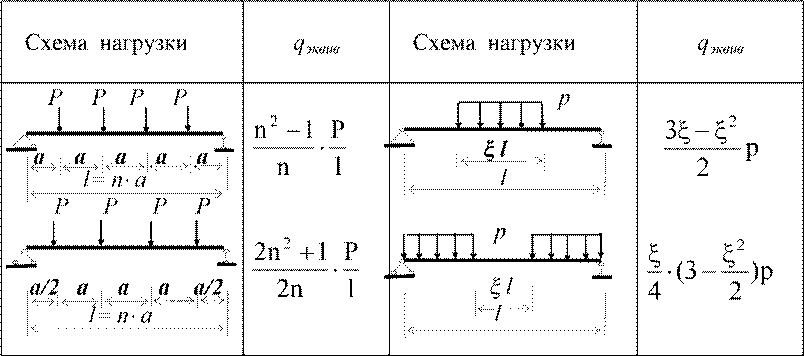
Пример.  Построить эпюры изгибающих моментов  и  поперечных сил в трех-пролетной балке. Крайние пролеты загружены  распределенной нагрузкой интенсивностью q = 2кН/м, а средний - сосредоточенной силой P = 10кН.

Пролеты имеют длину  12 м (рис. 1).

Решение.   Вычисление опорных моментов.

Вычертим многопролётную балку в соответствии с заданными размерами и нагрузкой. Вначале расчёта приведем сосредоточенную нагрузку в среднем пролете к эквивалентной - равномерно распределенной, пользуясь при этом табл. 2:

n² -1 P 2² -1 10     q = = =1.25 кН/м. n l 2 12

Загружение каждого пролета будем  рассматривать в отдельности. В соответствии с табл. 3  получим  значения   опорных   моментов. 

Таблица 3               Опорные моменты в неразрезных балках                         при загружении равномерно распределенной нагрузкой                   (размерный  множитель q l²)       

Примечание: Положительный изгибающий момент  растягивает нижние волокна элемента

Вычисление  пролетных  моментов  и  поперечных  сил.