Изучение движения материальной точки и твёрдого тела по отношению к выбранной системе координат

Министерство образования и науки  Российской федерации

Санкт-Петербургский государственный Инженерно-Экономический Университет

Контрольная работа №1

По Теоретическим основам прогрессивных технологий

Выполнила:                                                                                                              Принял:

Студентка группы 334                                                                                           Иванов Ю.А.

ФИСвЭУ

Соболева И.

Санкт-Петербург

2004

Задания:

1. r = r(t) - ?
2. x = x(t),  y = y(t), z = z(t) - ?
3. ,  - ?
4. ,  - ?
5. Равномерное прямолинейное движение

,  - ?

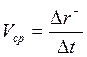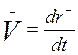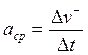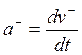6. Равнопеременное движение

 - ?

 - ?

 - ?

в векторном виде:

 - ?

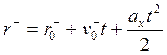в проекциях:

 - ?

 - ?

6. Задача. По прямолинейной дороге в одном направлении движутся два автомобиля согласно следующим формулам : ,. В какой момент времени они встретятся, если двигаться они начали одновременно? Определить скорость.

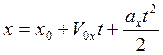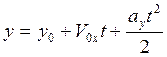Механика изучает движение материальной точки и твёрдого тела по отношению к выбранной системе координат ( неподвижную, связанную с Землёй, и подвижную, связанную с твёрдым телом).

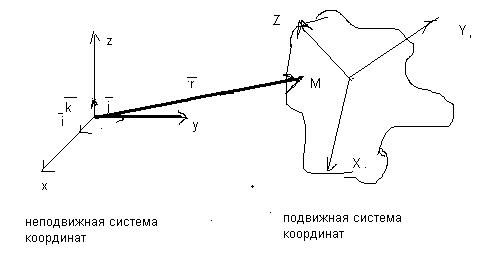
В векторном виде закон движения материальной точки выглядит следующим образом: r = r(t), откуда следует, что скорость и ускорение в векторном виде можно представить следующим образом: 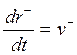,  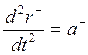  . Причём последнюю формулу мы можем в записать в виде 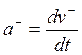.   Отсюда же можно узнать и среднюю скорость и среднее ускорение,.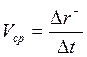

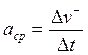Если применить координатный способ для описания материальной точки М, то получим следующее:

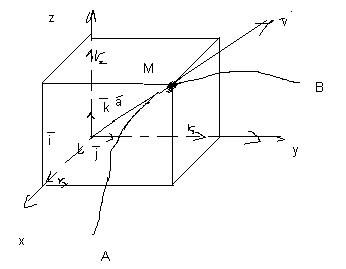В данный момент времени

                                                                       

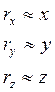
В декартовой системе координат 3 уравнения описывают уравнение движения

x = x(t),  y = y(t), z = z(t).

Быстрота изменения уравнения движения материальной точки М называется скоростью.

При движении материальной точки различают равномерное и равнопеременное движение, при этом линейная скорость V  может быть постоянной или переменной. При  равномерном прямолинейном движении скорость считают постоянной, поэтому пройденное расстояние считают по формуле ,v=const.

При равнопеременном движении ускорение а  считают константой, тогда врезультате разделения переменных и интегрирования левой и правой части получим значение текущей линейной скорости:

а = const

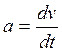, dv = adt

 , где  - начальная скорость. Проектируя это уравнение на оси координат, получим следующее:  

                                      

 В случае движения материальной точки в декартовой системе координат  уравнение

 проектируется на оси следующим образом:

,

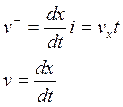в результате интегрирования: 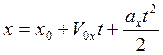. Эта формула характеризует равнопеременное движение точки М вдоль оси x. Причём равнопеременность движения

обуславливается знаком “+” / ”-“ перед ускорением (“+”- равноускоренное движение, “-“ – равнозамедленное движение).

При проектировании исходного уравнения  на ось y и аналогичных действиях получим формулу, которая характеризует равнопеременное движение точки М вдоль оси y: .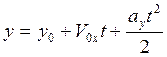

В векторном виде эти уравнения, характеризующие равнопеременное движение точки М можно записать: .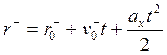

7.  Задача:  по прямолинейной дороге в одном направлении движутся 2 автомобиля согласно уравнениям:

x₁=25+5t (м)

x₂=13+19t (м)

В какой момент времени они встретятся, если двигаться они начали одновременно? Определить скорость.

V₀₁=(25+5t)′                   V₀₂=(13+19t)′

V₀₁= 5 (м/с)                              V₀₂=19 (м/с)

Момент встречи:

          25+5t=13+19t

          12=14t

          t= (c)

Ответ: Скорости равны 5 и 19 м/с соответственно. А встреча произойдет через 6/7 с.