


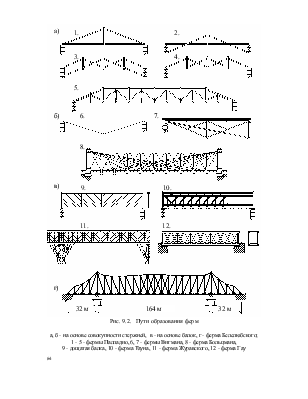




























Обратим внимание на то, что вектор R непосредственно в расчет не входит. Его можно было не находить, а сразу построить прямые N3 и N4 соответственно из начала N2 и конца силы P2.
Очевидно, обходя все остальные узлы в указанной последовательности, можно определить усилия во всех стержнях фермы. В последнем узле (V) все силы будут уже известны и его равновесие - проверка графического решения.
Рассматривая равновесие каждого узла в отдельности, в конце концов можно определить все усилия, но графическое решение при этом будет очень громоздким, одну и ту же силу придется чертить несколько раз. Идея графического метода, но в более компактной простой форме получила воплощение в диаграмме Кремоны - Максвелла. При ее построении будем придерживаться следующих правил. Следуя рекомендациям авторов, пространства между силами и стержнями обозначим полями; внешними (между внешними силами) A, B, C, D и внутренними (между стержнями) 1, 2, 3. При этом каждую силу можно обозначать полями, между которыми она расположена. Сила P2, например, будет обозначаться A-B, а сила N1 - D-1 и т.п.
Выберем направление обхода узлов и контура фермы, например, по часовой стрелке, и будем ему следовать. Также начнем решение с узла I. На него действуют сила D-A (P1) и неизвестные усилия в стержнях 1-D и A-1 (соответственно N1 и N2). Отложим в масштабе сил вектор D-A. Из конца D проведем луч, параллельный 1-D, а из конца A - луч, параллельный A-1. На пересечении лучей получим точку 1. Построение точно совпадает с описанным ранее (рис.9.14, б), значит, длина отрезка A-1 является усилием N2 , а отрезка 1-D - усилием N1 .
Рассматривая узел II, продолжим начатые построения. Из точки A по направлению силы P2 проведем луч и отложим величину силы P2 в масштабе по этому лучу, конец вектора обозначит точку B. Обходя узел II по часовой стрелке, найдем поле 2. Для этого из точки 1 проведем луч, параллельный стержню 2-1, а из точки B - луч, параллельный B-2, на их пересечении получим точку 2. Многоугольник AB21 точно совпадает с многоугольником, составленным силами N2, P2, N3, N4 (рис. 9.19, д) и, следовательно, отрезок 1-2 определяет усилие N3, а отрезок b-2 - N4 .
Подобным образом находятся точки C и 3. Полная диаграмма усилий показана на рисунке 9.14, ж.
Построение диаграммы удобно разбить на два этапа:
- построить многоугольник внешних сил, обходя только внешний контур фермы по внешним полям (здесь все силы известны);
- на основе многоугольника внешних сил, начиная обход с точки, которая относится к узлу с двумя стержнями, найти все внутренние поля и определить усилия в стержнях фермы.
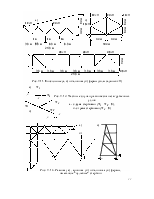
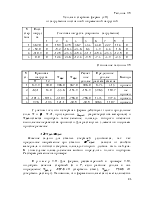
П р и м е р 9.6. Определить графически усилия в стержнях фермы
(рис. 9.15, а).
Р е ш е н и е. Опорные реакции определим из условия равновесия фермы аналитически:
S x = 0 fi Hа = 40 кН,
S mа= 0 fiVв = (60 4 +40 4)/8 = 50 кН,
S mв= 0 fiVа= (60 4 + 40 8 - 40 4)/8 = 50 кН.
Обозначим в соответствии с принятыми правилами внешние и внутренние поля (рис. 9.15, б). Построение диаграммы начнем с многоугольника внешних сил bcdfk. Так как система находится в равновесии, многоугольник должен получиться замкнутым (рис. 9.15, в). Затем на этом же чертеже построим диаграмму внутренних усилий в стержнях фермы, рассматривая узлы в последовательности, указанной на рисунке 9.15, б цифрами в скобках. (Узел 6 используем для контроля вычислений.) Полностью диаграмма приведена на рисунке 9.15, в.
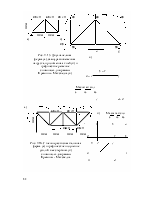
П р и м е р 9.7. (для самостоятельного решения). Определить усилия в ферме на рисунке 9.16. (Диаграмма усилий приведена на рисунке 9.16, б).
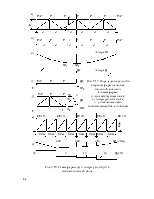
С п о с о б п л и т н о - б а л о ч н о й а н а л о г и и
Для оперативного анализа усилий в стержнях ферм часто прибегают к плитно-балочной аналогии. При достаточных навыках использование такой аналогии дает вполне удовлетворительные по точности результаты оценки рабочего состояния. При этом протяженные фермы, у которых один габаритный размер больше двух других, заменяются соответствующей балкой или плитой (пластиной), если один размер (высота) мал по сравнению с двумя другими (например, структура). Вначале получают усилия в соответствующей балке или плите (методика их расчета разобрана в главе 10), а затем путем простейших пересчетов - усилия в стержнях ферм. Разберем этот способ на примерах.
Для фермы, изображенной на рисунке 9.17 составим соответствующую балку, то есть такую, пролет которой равен пролету фермы, а точки приложения нагрузки соответствуют точкам пересечения линий действия нагрузок на ферму с осью балки. Для этой балки построим эпюры M и Q (рис. 9.17, б).
Если провести сечение (например, 1-1) и рассмотреть силы, действующие
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.