Строительство и архитектура \ Железобетонные конструкции

Испытание железобетонной балки (Б-1) на изгиб с разрушением ее по нормальному сечению, страница 3

åY = 0 ® Rs,n×As = Rb,n×b×x + Rsc,n×As¢.                                (2)

При этом балка должна быть запроектирована так, что полностью используются прочностные свойства арматуры растянутой (Rs,n) и сжатой (Rsc,n), т.е. соблюдается условие:

x =  £ x R ,                                                          (3)

где x R - граничное значение относительной высоты сжатой зоны, которое можно принять по табл. 4.

Таблица 4

Значение коэффициента x R

класс арматуры

класс бетона

B15

B20

AII

0,640

0,613

AIII

0,608

0,581

Рекомендуется следующая последовательность расчета:

§  используя формулу (2), определить значение x;

§  проверить выполнение условия (3);

§  при x > 2a¢ определить Мlim по формуле (1);

§  при x < 2a¢ определить Мlim по формуле (1), приняв As¢ = 0;

§  определить предельную теоретическую разрушающую нагрузку по формуле:

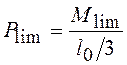 (н).

Здесь и в дальнейших расчетах сопротивления принимаются в Н/см2, для этого значения в МПа умножаются на (100); размеры - в см, нагрузка в Н, изгибающие моменты в Н×см.

2. Определение значения теоретического момента образования

     трещин (Мcrc)

В основу расчета положена cтадия I®Ia (Рис.2).

 


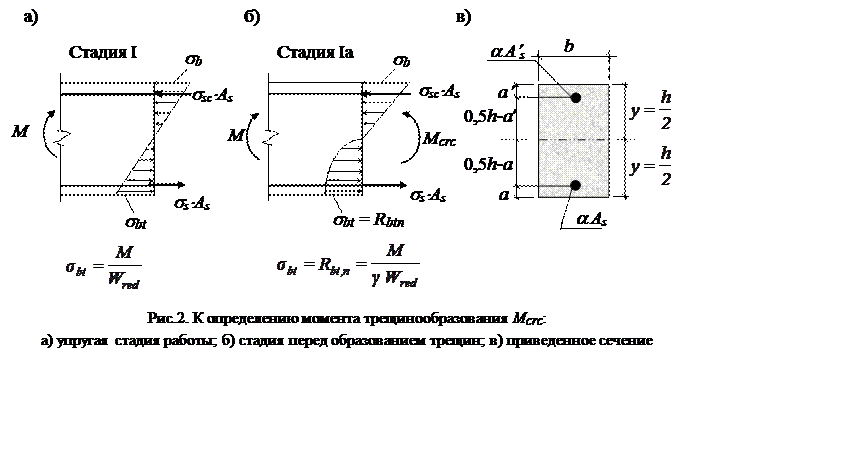
Рекомендуется определять момент образования трещин Mcrc с использованием следующих формул:

,                                               (4)

где   - упруго-пластический момент сопротивления сечения по растянутой зоне;

 - коэффициент, учитывающий пластические свойства растянутого бетона, для прямоугольного сечения может быть принят равным 1,75;

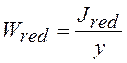 - момент сопротивления приведенного сечения, ;

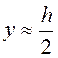 - момент инерции приведенного сечения -

;                                                 (5)

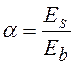 - коэффициент приведения.

3. Определение теоретической ширины раскрытия трещин acrc

В основу расчета на раскрытие трещин и по деформациям положена стадия II.

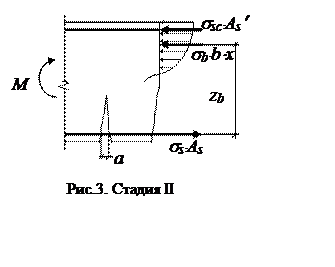
Расчет производится при условной нормативной нагрузке:

           .

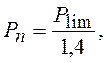
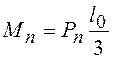Ширина раскрытия трещин на уровне центра тяжести арматуры определяется по формуле:

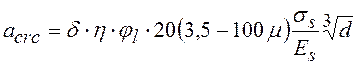,       (6)

где , ,  - коэффициенты соответственно, учитывающие вид напряженного состояния (изгиб), вид арматуры (стержневая), длительность воздействия нагрузки (нагрузка кратковременная);

- диаметр растянутой арматуры (при различных диаметрах принимается средний);

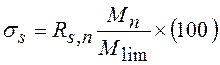 - напряжения в растянутой арматуре при нормативной нагрузке, н/см2;

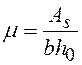 - коэффициент армирования.

4. Расчет прогиба балки

Значение прогиба в середине балки определяют по формуле:

, где  - коэффициент, зависящий от загружения и расчетной схемы, для данной балки ;

- кривизна балки, определяемая по формуле 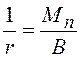, где B - жесткость изгибаемого элемента. Так как вычисление жесткости изгибаемого элемента Bдовольно трудоемко, допускается использовать эмпирическую формулу:

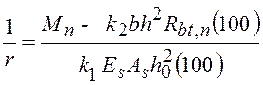,                                   (7)

где  - коэффициенты, определяемые по табл. 5 при значениях   .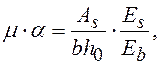

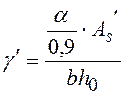Таблица 5

Значения коэффициентов k1,  k2

g¢

m×a

0,02

0,04

0,07

0,10

0,15

0,20

0,30

0,40

0,50

0,04¸0,2

0,2¸0,5

k1

k2

0

0,59

0,53

0,47

0,43

0,39

0,34

0,29

0,25

0,23

0,22

0,23

0,2

0,63

0,59

0,55

0,53

0,49

0,44

0,37

0,32

0,28

0,27

0,28

k3

0

-

1,05

0,98

0,93

0,90

0,8

-

-

0,2

-

1,09

1,05

0,98

0,93

0,87

0,75

-

ПРИЛОЖЕНИЕ II

ТЕОРЕТИЧЕСКИЕ РАСЧЕТЫ БАЛКИ БН-1

1.  Определение прочности балки в нормальном сечении (Mlim)

Этот расчет можно не производить, если в балках Б-1 и БН-1 приняты одинаковые геометрические параметры, армирование, класс бетона, несущая способность этих балок одинакова:

Скачать файл