Испытание железобетонной балки (Б-1) на изгиб с разрушением ее по нормальному сечению, страница 2

По опытным данным необходимо:

§  произвести обработку результатов и построить эпюры нормальных и касательных напряжений в бетоне - до появления трещин, после появления трещины и роста прогиба, перед разрушением. Значения напряжений в бетоне  определить с помощью диаграммы ¸, ;

§  составить карту трещин и изобразить характер разрушения балки;

§  построить график прогибов балки в зависимости от величины изгибающего момента. График позволяет отметить наличие неупругих деформаций в бетоне и арматуре в момент "образования трещин";

§  определить значение разрушающего момента и описать характер разрушения балки;

§  определить прогиб балки и ширину раскрытия трещин при условной нормативной нагрузке.

2.1.4. Анализ результатов испытания балки

1.  Необходимо зафиксировать при испытании балки последовательно расчетные стадии:

cтадию Iа - до образования трещин, P_crc, M_crc;

cтадию II - раскрытия трещин, роста прогиба;

стадию III - разрушения, P_lim, M_lim.

2.  Дать объяснение, какие ведутся расчеты по этим стадиям и их цель; как различаются расчетные формулы при расчете на прочность при испытании конструкции и при проектировании конструкции.

3.  Провести сравнение опытных и теоретических (расчетных) значений моментов трещинообразования (M_crc), разрушающих моментов (M_lim), прогибов балки (f):

; ; .

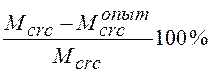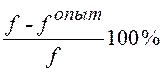Хорошая сходимость результатов испытания и расчета считается, если результат, полученный по вышеприведенным формулам, не превышает 15¸20%.

2.2. Лабораторная работа №2:

          Испытание предварительно напряженной балки (БН-1)

          на изгиб с разрушением по  нормальному сечению

Цель работы: исследование прочности, трещиностойкости и деформативности изгибаемого элемента с предварительным напряжением.

При этом ставятся задачи:

§  исследовать работу балки БН-1 во всех стадиях (I®Ia®II®III) напряженно-деформированного состояния и выявить влияние предварительного напряжения на прочность, жесткость, трещиностойкость;

§  выполнить теоретические расчеты и сравнить их с опытными данными;

§  сравнить данные, полученные в лабораторных работах №1 и №2.

2.2.1. Исходные данные и методика испытания

Для сравнения результатов испытания балок Б-1 и БН-1 геометрические параметры, армирование, прочностные, деформативные характеристики материалов балок и методика испытания должны быть приняты одинаковыми (см. п.п. 2.1.1 - 2.1.3).

Балка БН-1 изготавливается с предварительным напряжением, начальные контролируемые напряжения в продольной напрягаемой арматуре  задаются преподавателем.

Теоретические расчеты выполняются в соответствии с положениями, изложенными в Приложении 1, цель этих расчетов определить:

§  величину предельного изгибающего момента, воспринимаемого сечением балки БН-1;

§  величину момента трещинообразования ;

§  величину ширины раскрытия трещин при нормативных нагрузках ;

§  прогиб балки перед разрушением .

При определении нормальных  напряжений в бетоне  при испытании балки по показаниям приборов следует учитывать фактические напряжения, равные сумме , где  - предварительные напряжения в бетоне при обжатии (определение  см. теоретические расчеты, Приложение 1).

2.2.2. Анализ результатов испытаний балки БН-1

1.  Необходимо зафиксировать при испытании балки БН-1последовательно расчетные стадии:

cтадию Iа - до образования трещин, зафиксировать величины усилий

P_crc, M_crc;

cтадию II - раскрытия трещин, роста прогиба при P_n, M_n;

стадию III - разрушения, зафиксировать величины усилий P_lim, M_crc; установыть причину и характер разрушения.

2.  Сравнить эти стадии с соответствующие им величины мометов при испытании балок БН-1, Б-1. Сравнить величины M_crc, M_lim, ,f для балок БН-1, Б-1, определенные по соответствующим формулам, сделать вывод о влиянии усилия обжатия Р₂:

-  на несущую способность;

-  на трещиностойкость;

-  на величину прогиба.

3.  Провести сравнение для балки БН-1 опытных и теоретических (расчетных) значений моментов трещинообразования (M_crc), разрушающих моментов (M_crc), прогибов балки (f):

; ; .

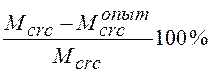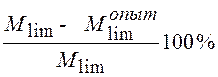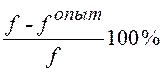ПРИЛОЖЕНИЕ 1. ТЕОРЕТИЧЕСКИЕ РАСЧЕТЫ БАЛКИ Б-1

1. Определение прочности балки в нормальном сечении (М_crc)

Для определения предельного изгибающего момента, воспринимаемого сечением перед разрушением, принимается стадия III - стадия разрушения (рис. 1,г). Из условий равновесия получаем:

åМ = 0 ® М_lim = R_b,n×b×x×(h₀- 0,5x)×(100) + R_sc,n×A_s¢×(h₀ - a¢)×(100);    (1)