3.2 Использование метрики, основанной на угловом расстоянии, для задач классификации
Необходимо классифицировать данные о доле отраслей в объеме промышленного выпуска.
Таблица 2.1 Доля отраслей в объеме промышленного выпуска
|
Электроэнергетическая |
Машиностроительная |
||
|
№ |
ось x |
ось y |
|
|
1 |
Гродненская |
6,9 |
11,5 |
|
2 |
Витебская |
11,1 |
20,1 |
|
3 |
Минск и Минская область |
21,3 |
34,2 |
|
4 |
Гомельская |
20,5 |
22,1 |
|
5 |
Брестская |
9,7 |
13,4 |
|
6 |
Могилевская |
18,2 |
29,4 |
|
R |
Радиус |
14,1 |
22,9 |
Примечание — Источник: [18]
Переведем данные в полярные координаты:
Таблица 3.2 Данные в полярных координатах
|
Полярные координаты |
|||
|
r |
y/x |
угол(рад) |
угол(град) |
|
13,411 |
1,667 |
1,030 |
59,036 |
|
22,961 |
1,811 |
1,066 |
61,091 |
|
40,291 |
1,606 |
1,014 |
58,085 |
|
30,144 |
1,078 |
0,823 |
47,151 |
|
16,542 |
1,381 |
0,944 |
54,100 |
|
34,577 |
1,615 |
1,016 |
58,241 |
|
26,850 |
1,621 |
1,018 |
58,323 |
Примечание — Источник: собственная разработка
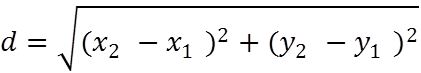 Вычисляя
расстояние между объектами для каждого возможного случая по формуле
Вычисляя
расстояние между объектами для каждого возможного случая по формуле
(1)
Получим следующие результаты:
Таблица 2.3 Суммы расстояний групп по три объекта
|
Евклидова метрика |
||||||
|
Точки |
Расстояние |
Случай |
Представление |
Сумма первой скобки |
Сумма второй скобки |
Сумма общая |
|
1,2 |
9,571 |
1 |
{(1,2,3);(4,5,6)} |
53,856 |
39,640 |
93,495 |
|
1,3 |
26,882 |
2 |
{(1,2,4);(3,5,6)} |
36,424 |
47,648 |
84,072 |
|
1,4 |
17,243 |
3 |
{(1,2,5);(3,4,6)} |
19,799 |
25,494 |
45,293 |
|
1,5 |
3,384 |
4 |
{(1,2,6);(3,4,5)} |
42,440 |
49,811 |
92,250 |
|
1,6 |
21,168 |
5 |
{(1,3,4);(2,5,6)} |
56,252 |
36,663 |
92,914 |
|
2,3 |
17,403 |
6 |
{(1,3,5);(2,4,6)} |
54,082 |
28,965 |
83,046 |
|
2,4 |
9,610 |
7 |
{(2,3,5);(1,4,6)} |
48,063 |
46,065 |
94,128 |
|
2,5 |
6,845 |
8 |
{(2,3,6);(1,4,5)} |
34,817 |
34,495 |
69,312 |
|
2,6 |
11,700 |
9 |
{(2,4,5);(1,3,6)} |
30,323 |
53,765 |
84,088 |
|
3,4 |
12,126 |
10 |
{(2,3,4);(1,5,6)} |
39,139 |
42,670 |
81,809 |
|
3,5 |
23,816 |
|||||
|
3,6 |
5,714 |
|||||
|
4,5 |
13,868 |
|||||
|
4,6 |
7,654 |
|||||
|
5,6 |
18,118 |
|||||
Примечание — Источник: собственная разработка
Используем формулу 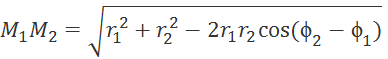 (2) для нахождения разности расстояний между кластерами,
используя угловую метрику.
(2) для нахождения разности расстояний между кластерами,
используя угловую метрику.
Таблица 2.4 Классификация объектов на основе угловой метрики
|
Угловая метрика |
||||||
|
Точки |
Расстояние |
Случай |
Представление |
Сумма первой скобки |
Сумма второй скобки |
Разность по модулю |
|
R,1 |
13,476 |
1 |
{(R1,R2,R3);(R4,R5,R6)} |
30,969 |
21,587 |
9,382 |
|
R,2 |
4,015 |
2 |
{(R1,R2,R4);(R3,R5,R6)} |
20,931 |
31,625 |
10,694 |
|
R,3 |
13,478 |
3 |
{(R1,R2,R5);(R3,R4,R6)} |
27,848 |
24,709 |
3,139 |
|
R,4 |
3,440 |
4 |
{(R1,R2,R6);(R3,R4,R5)} |
25,283 |
27,273 |
1,990 |
|
R,5 |
10,356 |
5 |
{(R1,R3,R4);(R2,R5,R6)} |
30,393 |
22,163 |
8,230 |
|
R,6 |
7,792 |
6 |
{(R1,R3,R5);(R2,R4,R6)} |
37,310 |
15,246 |
22,063 |
|
7 |
{(R2,R3,R5);(R1,R4,R6)} |
27,849 |
24,707 |
3,142 |
||
|
8 |
{(R2,R3,R6);(R1,R4,R5)} |
25,285 |
27,272 |
1,987 |
||
|
9 |
{(R2,R4,R5);(R1,R3,R6)} |
17,811 |
34,745 |
16,935 |
||
|
10 |
{(R2,R3,R4);(R1,R5,R6)} |
20,932 |
31,624 |
10,692 |
||
Примечание — Источник: собственная разработка
Таким образом, как видно из таблиц (2.3) и (2.4) оптимальный случай классификации, при котором попарное Евклидово расстояние между объектами минимально (случай 3) не всегда соответствует минимальному расстоянию между объектами, рассчитанному в метрике, основанной на угловом расстоянии. Такое заключение позволяет нам более гибко подходить к задаче анализа и классификации объектов по определенному признаку. Данный метод может оказаться полезным также в задачах размещения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.