МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Белорусский государственный экономический университет
,
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
ПО ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЕ
И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Учебно-методическое пособие для студентов экономических специальностей
МИНСК 2009
Предлагаемые задачи предназначены для контролируемой самостоятельной работы студентов. Результаты проверки выполненного индивидуального задания дают возможность оценить качество усвоения студентами учебного материала.
Варианты 1 – 25 содержат задания стандартного уровня сложности, варианты 26 – 30 – повышенного уровня сложности.
В пособии также приведены решения типового варианта.
Задание 1. Даны матрицы A,B,C. Найти те из произведений AB, BA, AC, CA, BC, CB, которые определены.
|
⎛ 1 ⎜ 4. A= −2 ⎜ ⎜ 5 ⎝ |
3⎞ ⎟ ⎛ 2 0 , B=⎜ ⎟ 4 1⎟⎠ ⎝ |
1 −1 |
0 ⎞ ⎟, C =(3 3⎠ |
2 |
4). |
|
⎛ 1 ⎞ ⎜ ⎟ ⎛2 −3 5⎞ 1. A= −2 , B=⎜ ⎟, C =(0 −1 3). ⎜ ⎟ |
|
|
⎜ 4 ⎟⎠ ⎝−4 2 1⎠ ⎝ |
|
|
⎛−2 4 ⎞ ⎛ ⎞1 ⎜ ⎟ ⎜ ⎟ ⎛1 2. A=⎜ 3 −1⎟, B=⎜ ⎟3 , C =⎝⎜3 ⎜ 0 2 ⎟ ⎜ ⎟⎝ ⎠1 ⎝ ⎠ |
−2 0⎞ ⎟. −4 5⎠ |
|
⎛ ⎞3 ⎛−1 0⎞ ⎜ ⎟ ⎜ ⎟ 3. A= 1 , B= 2 −3 , C=(5 ⎜ ⎟ ⎜ ⎟ ⎜ ⎟2 ⎜⎝ 1 4 ⎟⎠ ⎝ ⎠ |
0 3). |
⎛ 3 ⎞
⎛5 −3 2⎞ ⎜ ⎟
5. A=(4 −2 1), B=⎜1 2 −4⎠⎟, C =⎝⎜⎜−01⎠⎟⎟.
|
⎛ 0 6. A=⎜ ⎝−2 |
1 4 |
⎛ ⎞1 ⎛2 3 ⎞ ⎜ ⎟ ⎜ 1⎟,B=⎜ ⎟2 ,C =⎜⎜04 ⎠ ⎜ ⎟5 ⎝ ⎝ ⎠ |
0 ⎞ ⎟ −1 . ⎟ 1 ⎟⎠ |
⎝
⎛2 −3⎞ ⎛3⎞
7. A=(1 2 3), B=⎜⎜ 5 1 ⎟⎟, C =⎜⎜0⎟⎟.
⎜⎝−4 2⎟⎠ ⎜⎝4⎟⎠
⎛ 2 1⎞
|
B=(3 |
⎛0 2 1), C =⎜ ⎝4 ⎛ 5 ⎞ |
−4 −2 |
2⎞ ⎟. 3⎠ |
|
⎛3 9. A=⎜ ⎝−2 |
0 −1⎞ ⎜ ⎟ ⎟, B= −⎜ 3⎟, C = −( 4 2 5). |
|
|
4 1⎠ ⎜ 2 ⎟⎠ ⎝ |
||
|
⎛1 10. A=⎜ ⎝ 2 |
⎛−1 4⎞ ⎛0⎞ −3 4⎞ ⎜ ⎟ ⎜ ⎟ 0 1 ⎟, B= 4 2⎟, C =⎜1⎟⎟. ⎜ ⎠ ⎜ 0 3⎟⎠ ⎜⎝2⎠ ⎝ |
|
|
⎛2 ⎜ 11. A= −1 ⎜ ⎜ 4 ⎝ |
−3⎞ ⎛ ⎞1 ⎟ ⎜ ⎟ 0 , B= 0 , C =(3 −5 3). ⎟ ⎜ ⎟ 1 ⎟⎠ ⎜ ⎟⎝ ⎠2 |
|
|
12. A=(4 |
⎛1 0⎞ 1 −3), B=⎜⎜2 3⎟⎟, C =⎛⎜−11 03 ⎜0 1⎟⎠ ⎝ ⎝ |
−4⎞ ⎟. 2 ⎠ |
|
⎛ 1 ⎞ ⎜ ⎟ ⎛0 −3 2⎞ 13. A= −2 , B=(3 5 −1), C =⎜ ⎟. ⎜ ⎟ 4 1 −5⎠ ⎜⎝ 4 ⎟⎠ ⎝ ⎛−1 2⎞ ⎛4⎞ ⎜ ⎟ ⎛0 1 −2⎞ ⎜ ⎟ 14. A= 0 1 , B=⎜−3 0 1⎟⎠, C =⎜⎜53⎠⎟⎟. ⎜ ⎟ ⎜ 4 3⎟⎠ ⎝ ⎝ ⎝ |
||
⎜ ⎟
⎜ ⎟
|
⎛ 0 ⎞ ⎜ ⎟ |
⎛ 1 ⎜ |
3 ⎞ ⎟ |
|
15. A= −3⎟, B= −( 5 1 ⎜ ⎜ ⎝ 2 ⎠⎟ ⎛−3 1 0⎞ 16. A=⎜ ⎟, B=(0 ⎝1 −4 1⎠ |
4), C= −⎜ 2 5⎟. ⎜ ⎝4 −1⎟⎠ ⎛ 2 1 −2), C=⎜⎜ 0 ⎜−1 ⎝ |
1⎞ ⎟ 3 . ⎟ 4⎟⎠ |
⎜⎝
3 4⎟⎠
⎛−3⎞
⎜ ⎟ ⎛ 2 3 0 ⎞
|
⎝ 1 ⎠ |
||
|
⎛ ⎞2 ⎜ ⎟ ⎛1 2 18. A= 0 , B=⎜ ⎜ ⎟ ⎜ ⎟1 ⎝0 1 ⎝ ⎠ |
⎛−2 1⎞ 0⎞ ⎜ ⎟ ⎟, C = −1 3 . 2⎠ ⎜⎜−3 1⎟⎟⎠ ⎝ |
|
|
⎛ 1 0⎞ ⎜ ⎟ 19. A= 3 4 , B=(3 ⎜ ⎟ ⎜ ⎟ ⎝−2 3⎠ |
⎛2⎞ 2 1), C =⎜⎜0 .⎟⎟ ⎜3⎟⎠ ⎝ |
|
|
⎛ 1 ⎛ 2 3 1 ⎞ ⎜ |
0 ⎞ ⎟ |
|
|
20. A=(3 |
4 2), B=⎜ ⎝0 |
⎟, C = −2 −1 4⎠ ⎜⎜ 5 ⎝ |
|
⎛2 21. A=⎜ ⎝1 |
−1 0⎞ ⎟, B=(3 4 −5⎠ |
⎛ ⎞4 −2 4), C =⎜ ⎟⎜ ⎟3 . ⎜ ⎟ |
17. A=(1 −2 −4), B=⎜⎜ 5 ⎟⎟, C=⎜⎝−5 4 1⎟⎠.
1 .
⎟ −1⎠⎟
⎝ ⎠1
⎛ ⎞1 ⎛3
⎜ ⎟ ⎜
22. A= 0 , B= 1
⎜ ⎟ ⎜
⎝ ⎠⎜ ⎟2 ⎝⎜4
23. A=(1 −3 2),
⎛ 3 1 0 ⎞
−1⎞
|
0 , C =⎜ ⎟ 1 4 −2⎠⎟ ⎝ ⎛ ⎞2 ⎛ 3 ⎜ ⎟ ⎜ B= 1 , C = −2 ⎜ ⎟ ⎜ ⎜ ⎟0 ⎜⎝ 4 ⎝ ⎠ ⎛ 0 2 ⎞ |
⎟. 3 ⎠ 0 ⎞ ⎟ −4 . ⎟ 1 ⎟⎠ |
|
⎜ ⎟ |
|
⎟ ⎛0 −2 1⎞
24. A=⎜−1 2 4⎠⎟, B= −⎝⎜⎜ 21 −31⎠⎟⎟, C =(4 1 0).
⎝
⎛ 3 ⎞
⎜ ⎟ ⎛4 −2 0⎞
25. A=⎜ 0 , B=⎜ ⎟, C =(2 −3 5). ⎜⎝−1⎟⎟⎠ ⎝ 1 2 4 ⎠
⎛ ⎞2
26. A=⎜ ⎟,
⎛−52 04 73⎞⎠ B=(1 −4 3), C =⎜ ⎟⎜ ⎟⎜ ⎟⎝ ⎠60 .
⎝
⎛ 1 0 ⎞
⎛ 0 4 1⎞ ⎜ ⎟.
27. A=(1 −4 3), B=⎜ 2 −1 4⎟⎠ , C = −⎝⎜⎜ 43 −21⎠⎟⎟
⎝
⎛ 1 0⎞ ⎛2⎞
⎜⎜ 3 4 ⎟⎟, B=(3 2 1), C =⎜⎜0⎟⎟.
28. A=
⎜ −2 3⎠⎟ ⎝⎜3⎟⎠
⎝
⎛ ⎞1 ⎛2 −1⎞
29. A= 0 ,
⎝ ⎠⎜ ⎟ B=⎛⎜3 01 02⎞⎟⎠ , C =⎜⎜⎜ 13 −−43⎠⎟⎟⎟.
⎜ ⎟ 1
⎜ ⎟2 ⎝ ⎝
⎛ 5 0⎞
⎛3 −1 0 ⎞ B=(1 −3 2), C =⎜⎜ 2 3 ⎟⎟.
30. A=⎜⎝ 4 −2 ⎟⎠, ⎜⎝−1 6⎟⎠
1
Задание 2. 1 – 25. Вычислить определитель:
−1 −2 3 4−4 1 26 0 −1 1
2 0 1 −12 −1 22 −2 0 1
1. . 2. . 3.
3 −3 1 0−3 0 11 1 −3 3
4 2 1 −22 1 −24 1 −1 2
2 −2 0 33 −5 1 25 0 1
3 2 1 −10 1 −1 20 4 1
4. . 5. . 6. .
1 1 −2 13 1 −3 0−2 1 −4
3 4 −4 01 2 −1 24 3 −2
3 −1 2 12 −3 1−3 3 −6
4 1 2 03 −1 21 2 2
7. . 8. . 9.
−1 2 1 −1 2 0 1−4 6 2
5 0 4 2−1 2 02 −3 −2
1 −2 3−1 2 24 1 −6
2 1 −4−2 3 −2−10 −4 −2
10. . 11. . 12. .
3 −4 −14 0 12 −7 4 4 3 21 6 46 −5 2
1 3 15 1 43 6 −2 5
−1 2 20 −1 22 3 5 −1
13. . 14. . 15.
0 1 −24 2 21 0 6 4 3 −1 32 1 01 3 −2 0
6 3 −5 04 04 −3 5
2 0 −1 3−3 −2−6 2 4
16. . 17. . 18.
0 2 −1 47 2−1 7 1
4 3 −4 −35 −1−5 −2 3
3 2 1 54 12 3 2 1
5 4 −2 13 0−1 4 −1 2
19. . 20. . 21.
3 1 2 −2−5 −22 1 −2 3
2 0 1 4−2 −20 2 4 −2
3 5 4−4 1 30 4 4
2 −1 52 1 3−2 −8 1
22. . 23. . 24. .
0 2 12 2 41 2 −5
−2 3 01 4 57 −3 4
1 −3 7 −1
3 2 0 2
25.
2 1 4 −6
5 3 6 4
26 – 30. Решить уравнение:
5 −3 4 2−3
−2
x
−2 3 −7 −14 0 2
26.
= 20. 27. = 43. x 0 3 −17 2 04 −1 1 35 −1 −3
1 −2 3 −13 3 5 2
0 1 −4 32 3 x 0
28. = 30. 29. =18.
3 −4 1 x0 5 3 −2
4 3 −2 −16 −2 4 6
5 3 −4 1
0 x 2 −3
30. =16.
4 −2 1 1
2 0 1 −1
Задание 3. Решить систему уравнений матричным методом:
|
⎧ 3x1 +5x2 − x3 = 2, ⎪ 1. ⎨ x1 −3x2 + 2x3 = 3, ⎪ ⎩2x1 + 7x2 −3x3 = −1. |
⎧4x1 + x2 − x3 = −3, ⎪ 2. ⎨x1 − 2x2 +3x3 = −2, ⎪ 2x1 + x2 + x3 =1. ⎩ |
|
|
⎧x1 −3x2 + 2x3 = −3, ⎪ 3. ⎨5x1 − x2 +5x3 = 4, ⎪x1 − x2 +3x3 = −2. ⎩ |
⎧x1 + 2x2 + x3 = 4, ⎪ 4. ⎨3x1 −5x2 + 3x3 =1, ⎪2x1 + 7x2 − x3 =8. ⎩ |
|
|
⎧2x1 −3x2 + x3 = 5, ⎪ 5. ⎨ x1 +3x2 − x3 = 4, ⎪ x1 + x2 − x3 = −4. ⎩ |
⎧ 2x1 + x2 +3x3 = 3, ⎪ 6. ⎨ 4x1 + 2x2 +5x3 = 2, ⎪ ⎩3x1 + 4x2 + 7x3 = −1. |
|
|
⎧2x1 + 4x2 + x3 = 4, ⎪ 7. ⎨3x1 + 6x2 + 2x3 = 4, ⎪4x1 − x2 −3x3 = −4. ⎩ |
⎧x1 + x2 + x3 = −3, ⎪ 8. ⎨x1 − 2x2 + x3 = −6, ⎪x1 + x2 − 2x3 = 0. ⎩ |
⎧2x1 −3x2 + x3 = 2, ⎧2x1 −3x2 + x3 =17,
⎪ ⎪
9. ⎨x1 + 5x2 − 4x3 = −5, 10. ⎨5x1 + x2 −3x3 = −2,⎪⎩4x1 + x2 −3x3 = −4. ⎩⎪4x1 +3x2 + 2x3 =16.
⎧2x1 − 4x2 + 3x3 =1, ⎧x1 +3x2 − x3 = 4,
⎪ ⎪
11. ⎨x1 − 2x2 + 4x3 = 3, 12. ⎨2x1 −3x2 + x3 = 5,⎪⎩3x1 − x2 + 5x3 = 2. ⎪⎩x1 + x2 − x3 = −4.
⎧2x1 − x2 + x3 = 2, ⎧ x1 − 2x2 + 3x3 = 6,
⎪ ⎪
13. ⎨3x1 + 2x2 + 2x3 = −2, 14. ⎨2x1 +3x2 − 4x3 = 20,⎪⎩ x1 − 2x2 + x3 =1. ⎪⎩3x1 − 2x2 −5x3 = 6.
⎧x1 + 2x2 + 3x3 = 5, ⎧5x1 + 2x2 −9x3 = −6,
⎪ ⎪
15. ⎨2x1 − x2 − x3 =1, 16. ⎨ 5x2 −6x3 = −12,⎪⎩x1 + 3x2 + 4x3 = 6. ⎪⎩ 4x1 −5x2 = 6.
⎧2x1 −3x2 + 4x3 = −4, ⎧ 2x1 − x2 + x3 = 4,
⎪ ⎪
17. ⎨3x1 − 2x2 + 5x3 = −1, 18. ⎨ x1 +3x2 − x3 = 7,⎪⎩2x1 −3x2 −5x3 = −13. ⎪⎩3x1 − x2 − 4x3 =12.
⎧ x1 + 2x2 + 3x3 = 3, ⎧ x1 + x2 − x3 = 36,
⎪ ⎪
19. ⎨2x1 + 4x2 + 5x3 = 5, 20. ⎨−x1 + x2 + x3 = 7,⎪⎩4x1 +3x2 + 7x3 = 2. ⎪⎩ x1 + x2 − x3 =13.
⎧3x1 − x2 = 5, ⎧2x1 − 4x2 + 9x3 = 28,
⎪ ⎪
21. ⎨−2x1 + x2 + x3 = 0, 22. ⎨7x1 + 3x2 −6x3 = −1,⎪⎩2x1 − x2 + 4x3 =15. ⎪⎩7x1 + 9x2 −9x3 = 5.
⎧5x1 −9x2 + 4x3 = 7, ⎧x1 + 2x2 +3x3 = 4,
⎪ ⎪
23. ⎨7x1 −3x2 + 5x3 = 32, 24. ⎨3x1 −5x2 +3x3 =1,⎪⎩2x1 + 4x2 + 3x3 = 41. ⎩⎪2x1 + 7x2 − x3 = 8.
⎧ 2x1 − x3 = 3, ⎧3x1 + 4x2 + 7x3 = −1,
⎪ ⎪
25. ⎨ 2x1 + 4x2 − x3 =1, 26. ⎨−2x1 + 5x2 −3x3 =1,⎪⎩−x1 +8x2 + 3x3 = 2. ⎪⎩5x1 −6x2 +11x3 = −3.
⎧3x1 + 4x2 + 7x3 = −1, ⎧ x1 − 2x2 +3x3 = 6,
⎪ ⎪
27. ⎨−2x1 + 5x2 −3x3 =1, 28. ⎨2x1 +3x2 − 4x3 = 20,⎪⎩5x1 − 6x2 +11x3 = −3. ⎪⎩3x1 − 2x2 −5x3 = 6.
⎧x1 + x2 + x3 = 36, ⎧3x1 −5x2 +3x3 =1,
⎪ ⎪
29. ⎨2x1 − 3x3 = −17, 30. ⎨2x1 + 7x2 − x3 =8,
⎪⎩6x1 − 5x3 = 7. ⎪⎩x1 + 2x2 + x3 = 4.
Задание 4. 1 – 25. Найти ранг матрицы:
⎛2 3 1 −1⎞ ⎛1 2 3 −2⎞ ⎛1 2 −1 1 ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
3 1 4 2 2 −3 1 −4 5 1 2 1
1. ⎜ ⎟; 2. ⎜ ⎟; 3. ⎜ ⎟;
⎜1 2 3 −1⎟ ⎜1 9 8 −2⎟ ⎜4 −1 3 0 ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝1 −4 −7 5 ⎠ ⎝1 −12 −7 −2⎠ ⎝3 3 4 −1⎠
⎛1 2 3 1 ⎞ ⎛1 3 1 −3 ⎞ ⎛4 3 −1 1 ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
2 0 2 0 2 1 1 1 2 1 −3 3
4. ⎜ ⎟; 5. ⎜ ⎟; 6. ⎜ ⎟;
⎜3 2 5 1 ⎟ ⎜3 −11 −1 19 ⎟ ⎜1 1 1 −1⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝1 0 1 −2⎠ ⎝1 12 2 −16⎠ ⎝6 5 1 −1⎠
⎛1 −1 1 −1⎞ ⎛ 0 4 10 1 ⎞ ⎛ 2 1 11 2 ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
1 2 −3 2 4 8 18 7 1 0 4 −1
7. ⎜ ⎟; 8. ⎜ ⎟; 9.⎜ ⎟;
⎜1 1 −2 3 ⎟ ⎜10 18 40 17⎟ ⎜11 4 56 5 ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝2 −1 1 −3⎠ ⎝ 1 7 17 3 ⎠ ⎝ 2 −1 5 −6⎠
⎛ −1 2 3 4 ⎞ ⎛2 −1 4 0⎞ ⎛0 0 2 −1⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
0 1 −3 2 4 −2 0 5 0 2 4 −2
10. ⎜ ⎟; 11. ⎜ ⎟; 12. ⎜ ⎟;
⎜ 1 −3 0 −6⎟ ⎜8 −4 8 5⎟ ⎜1 3 −2 4 ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝−2 4 6 8 ⎠ ⎝6 −3 12 0⎠ ⎝1 6 4 1 ⎠
⎛24 14 17 15⎞ ⎛1 3 5 −1⎞ ⎛25 31 17 43 ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
23 13 16 14 2 −1 −3 4 75 94 53 132
13. ⎜ ⎟; 14. ⎜ ⎟; 15.⎜ ⎟; ⎜47 27 33 29⎟ ⎜5 1 −1 7 ⎟ ⎜75 94 54 134⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ 3 0 0 5 ⎠ ⎝7 7 9 1 ⎠ ⎝25 32 20 48 ⎠ ⎛8 −4 5 9 ⎞ ⎛5 2 −3 1 ⎞ ⎛1 2 3 4⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
1 −3 −5 −7 4 1 −2 3 2 3 4 5
16. ⎜ ⎟; 17. ⎜ ⎟; 18. ⎜ ⎟;
⎜7 −5 1 1 ⎟ ⎜1 1 −1 −2⎟ ⎜3 4 5 6⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝3 −1 3 5 ⎠ ⎝3 4 −1 2 ⎠ ⎝4 5 6 7⎠
⎛2 1 −3 1⎞ ⎛4 −5 2 6⎞ ⎛3 −1 3 5 ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
4 2 −6 2 2 −2 1 3 5 −3 2 1
19. ⎜ ⎟; 20. ⎜ ⎟; 21. ⎜ ⎟;
⎜6 3 −9 3⎟ ⎜6 −3 4 9⎟ ⎜1 −3 −5 −7⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝1 1 1 1⎠ ⎝4 −1 5 7⎠ ⎝7 −5 1 1 ⎠
⎛2 −1 3 5 ⎞ ⎛2 3 −4 1 ⎞
⎜ ⎟ ⎜ ⎟
4 −3 1 3 1 2 3 −4
22. ⎜ ⎟; 23. ⎜ ⎟;
⎜3 −2 3 5 ⎟ ⎜2 −5 8 −3 ⎟
⎜ ⎟ ⎜ ⎟
⎝4 −1 15 17⎠ ⎝5 26 −9 −10⎠
⎛ 2 −1 4 −2⎞ ⎛5 1 −1 7 ⎞
⎜ ⎟ ⎜ ⎟
−1 1 −3 −1 2 −1 −3 4
24. ⎜ ⎟; 25. ⎜ ⎟.
⎜ 4 −3 −1 0 ⎟ ⎜1 3 5 −1⎟
⎜ ⎟ ⎜ ⎟
⎝ 7 −4 4 −6⎠ ⎝7 7 9 1 ⎠
26 – 30. Найти ранг матрицы в зависимости от значения параметра λ:
⎛ 3 1 1 4⎞ ⎛−1 2 3 4 ⎞ ⎛2 −1 4 0⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ λ 4 10 1 0 1 λ 2 4 −2 0 λ
26. ⎜ ⎟; 27. ⎜ ⎟; 28. ⎜ ⎟;
⎜ 1 7 17 3⎟ ⎜ 1 −3 0 −6⎟ ⎜8 −4 8 λ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝ 2 2 4 3⎠ ⎝−2 4 6 8 ⎠ ⎝6 −3 12 0⎠
⎛1 2 −1 1 ⎞
⎜ ⎟ ⎛ 1 3 −1 2 ⎞
5 1 2 1 ⎜ ⎟
29. ⎜ ⎟; 30. 2 −1 λ 5 .
⎜⎜4 −1 λ 0 ⎟ ⎜⎜⎝1 10 −6 λ⎟⎟⎠
⎟
⎝3 −3 4 −1⎠
Задание 5. 1 – 25. Исследовать на совместность и решить систему линейных уравнений:
|
⎧ 2x x1 + 2 − x x3 + 4 =1, ⎪⎪3x1 − 2x2 + 2x3 − 3x4 = 2, 1. а) ⎨ ⎪ 5x x1 + 2 − x3 + 2x4 = −1, ⎪⎩ 2x x1 − 2 + x3 − 3x4 = 4. |
⎧ x1 + 2x2 + 3x x3 − 4 = 0, ⎪ x x1 − 2 + x3 + 2x4 = 4, ⎪ б) ⎨ ⎪x1 + 5x2 + 5x3 − 4x4 = −4, ⎪⎩x1 + 8x2 + 7x3 − 7x4 = −8. |
|
⎧4x1 + 3x2 − 3x x3 − 4 = 4, ⎪⎪3x x1 − 2 + 3x3 − 2x4 =1, 2. а) ⎨ ⎪ 3x x1 + 2 − x4 = 0, ⎩⎪5x1 + 4x2 − 2x3 + x4 = 3. |
⎧ x x1 − 2 + 2x3 + 2x4 = 2, ⎪⎪ 3x1 − 2x2 − x x3 − 4 = −1, б) ⎨ ⎪5x1 − 3x2 − 4x3 − 2x4 = −4, ⎩⎪7x1 − 4x2 − 7x3 − 5x4 = −7. |
|
⎧ x1 + 2x2 − x3 + x4 = −2, ⎪⎪ −2x1 − 3x2 + 2x x3 − 4 = 2, 3. а) ⎨ ⎪x1 + 3x2 − x3 +11x4 = −10, ⎩⎪x1 + 4x2 − x3 +18x4 = −18. |
⎧ 2x1 + 7x2 + 3x x3 + 4 = 6, ⎪⎪3x1 + 5x2 + 2x3 + 2x4 = 4, б) ⎨ ⎪ 9x1 + 4x2 + x3 + 7x4 = 2, ⎩⎪ x1 − 2x2 − x3 + x4 = −2. |
|
⎧3x1 + 2x2 + 2x3 + 2x4 = 2, ⎪2x1 + 3x2 + 2x3 + 5x4 = 3, ⎪ 4. а) ⎨ ⎪2x1 + 2x2 + 3x3 + 4x4 = 5, ⎪⎩ 7x x1 + 2 + 6x x3 − 4 = 8. |
⎧9x1 − 3x2 + 5x3 + 6x4 = 4, ⎪6x1 − 2x2 + 3x3 + 4x4 = 5, ⎪ б) ⎨ ⎪ 3x x1 − 2 + 3x3 + x4 = −8, ⎪⎩3x x1 − 2 + 2x3 + 2x4 = −1. |
|
⎧ 2x1 + 3x2 + 2x3 + 5x4 =1, ⎪⎪ x x1 + 2 + 4x3 + 3x4 =1, 5. а) ⎨ ⎪ x1 + 2x2 − 2x3 + 2x4 = 0, ⎩⎪5x1 + 8x2 + 2x3 +12x4 = 0. |
⎧3x1 + 2x2 + 2x3 + 2x4 = 2, ⎪ ⎪2x1 + 3x2 + 2x3 + 5x4 = 3, б) ⎨ ⎪ 9x x1 + 2 + 4x3 − 5x4 =1, ⎪⎩2x1 + 2x2 + 3x3 + 4x4 = 5. |
⎧ 2x1 + 3x2 − x3 + x4 = 5,
⎪ 3x x1 − 2 + 2x3 + x4 =1,
⎪
⎪ x1 + 2x2 + 3x3 + 4x4 = 6,
⎪⎩6x1 + 4x2 + 4x3 + 6x4 =1.
⎧ 2x x1 − 2 + x x3 − 4 = 3,
⎪⎪4x1 − 2x2 − 2x3 + 3x4 = 2,
⎪ 2x x1 − 2 + 5x3 − 6x4 =1,
⎪⎩ 2x x1 − 2 − 3x3 + 4x4 = 5.
⎧ 4x1 − 2x2 + 5x3 + 6x4 = 7,
⎪⎪ 2x x1 − 2 + 2x3 + 2x4 = 2,
⎪16x1 − 7x2 +16x3 +18x4 = 20, ⎪⎩ 4x x1 − 2 + 2x3 + 2x4 = 2.
⎧ 5x1 − 3x2 + 2x3 + 4x4 = 3,
⎪⎪ 4x1 − 2x2 + 3x3 + 7x4 =1,
⎪ 8x1 − 6x2 − x3 − 5x4 = 9,
⎩⎪7x1 − 3x2 + 7x3 +17x4 = 0.
⎧4x1 − 3x2 + 2x x3 − 4 = 8,
⎪3x1 − 2x2 + x3 − 3x4 = 7,
⎪
⎪ 2x x1 − 2 − 5x4 = 6,
⎪⎩5x1 − 3x2 + x3 − 8x4 =1.
⎧2x1 + 3x2 +11x3 + 5x4 = 2,
⎪ x x1 + 2 + 5x3 + 2x4 =1,
⎪
|
⎧ 3x1 + 4x2 + x3 + 2x4 = −3, ⎪3x1 + 5x2 + 3x3 + 5x4 = −6, ⎪ 10. а) ⎨ ⎪6x1 + 8x2 + 2x3 + 5x4 = −8, ⎪⎩3x1 + 5x2 + 3x3 + 7x4 = −7. |
⎧ x1 + 2x2 + 4x3 − 3x4 = 5, ⎪ 3x1 + 5x2 + 6x3 − 4x4 = 8, ⎪ б) ⎨ ⎪ 4x1 + 5x2 − 2x3 + 3x4 = −1, ⎪⎩3x1 + 8x2 + 24x3 −19x4 = 29. |
|
⎧ 2x1 − 5x2 + 3x x3 + 4 = 5, ⎪⎪3x1 − 7x2 + 3x x3 − 4 = −1, 11. а) ⎨ ⎪5x1 − 9x2 + 6x3 + 4x4 = 7, ⎪⎩ 4x1 − 6x2 + 3x x3 + 4 = 8. |
⎧ 2x1 − 4x2 + 5x3 + 3x4 = −3, ⎪ 3x1 − 6x2 + 4x3 + 2x4 =1, ⎪ б) ⎨ ⎪4x1 − 8x2 +17x3 +11x4 = −17, ⎪⎩ x1 − 2x2 +13x3 + 9x4 = −18. |
|
⎧ 3x1 + 4x2 + 2x3 − 2x4 =1, ⎪ ⎪6x1 − 5x2 + 2x3 + 4x4 = −4, 12. а) ⎨ ⎪ 9x x1 − 2 + 4x x3 − 4 =13, ⎪⎩ 3x1 − 9x2 + 3x4 = 8. |
⎧5x1 − 3x2 − 4x3 − 2x4 = −4, ⎪ 2x x1 − 2 − 3x3 − 3x4 = −3, ⎪ б) ⎨ ⎪ 3x1 − 2x2 − x x3 − 4 = −1, ⎪⎩ 4x1 − 3x2 + x3 + x4 =1. |
|
⎧ x x1 + 2 − 6x3 − 4x4 = 6, ⎪ 3x x1 − 2 − 6x3 − 4x4 = 2, ⎪ 13. а) ⎨ ⎪ 2x1 + 3x2 − 9x3 + 2x4 = 6, ⎩⎪3x1 + 2x2 + 3x3 + 26x4 = −7. |
⎧ 2x1 − 2x2 − x3 + x4 =1, ⎪⎪ x1 + 2x2 + x3 − 2x4 =1, б) ⎨ ⎪ 4x1 −10x2 − 5x3 + 7x4 =1, ⎪⎩2x1 −14x2 − 7x3 +11x4 = −1. |
⎪ 2x x1 + 2 + 3x3 + 2x4 = −3, ⎪⎩ x x1 + 2 − x3 + x4 = −3.
⎧ 2x x1 − 2 + 3x + 4x4 = 5,
⎪⎪ 4x1 − 2x2 + 5x3 + 6x4 = 7,
⎨
⎪ 6x1 − 3x2 + 7x3 + 8x4 = 9,
⎪⎩8x1 − 4x2 + 9x3 +10x4 =11.
⎧ x1 − 3x2 − 2x3 − 5x4 = −3,
⎪⎪3x1 − 2x2 − 3x3 − 4x4 = −5,
⎪ 3x1 + 5x2 + 7x4 = −1,
⎩⎪ 5x x1 − 2 − 4x3 − 3x4 = −7.
⎧ 2x1 + 2x2 − x3 + x4 = 2,
⎪⎪ 4x1 + 3x2 − x3 + 2x4 = 2,
⎪8x1 + 5x2 − 3x3 + 3x4 =12, ⎪⎩ 2x1 + 3x2 − 2x3 + x4 = 6. ⎧ x1 + 2x2 + 3x3 + 4x4 = 0,
⎪⎪ x1 − 2x2 − 3x3 − 4x4 = 2,
⎪ x1 + 3x3 + 4x4 = −1,
⎩⎪x1 + 3x2 + 6x3 + 8x4 = −1. ⎧2x1 + 2x x3 − 3x4 = −6,
⎪⎪ 3x x1 + + x3 + 2x4 = 0,
⎪ 2x1 − 2x2 + x4 = −3,
⎩⎪ x1 + 3x2 + x x3 − 4 = 2.
⎧5x1 + 6x2 − 2x + 6x4 = 5,
⎪ 2x1 + 3x2 − x3 + 2x4 = 2, ⎪
⎨
|
⎧ 2x1 − 3x2 + 3x3 + 2x4 = 3, ⎧x1 − 2x2 + 3x3 − 4x4 = 4, ⎪ 6x1 + 9x2 − 2x x3 − 4 = −4, ⎪⎪ x2 − x3 + x4 = −3, ⎪ 16. а) ⎨ б) ⎨ ⎪10x1 + 3x2 + 4x3 − 2x4 = 3, ⎪ x1 + 3x2 − 3x4 =1, ⎪⎩ 8x1 + 6x2 + x3 + 3x4 = −7. ⎪⎩ − 7x2 + 3x3 + x4 = −3. ⎧ x1 + 2x2 + 5x3 + 9x4 = 79, ⎧x1 + 2x2 + 3x x3 − 4 =1, ⎪3x1 +13x2 +18x3 + 30x4 = 263, ⎪⎪3x1 + 2x2 + x x3 − 4 =1, ⎪ 17. а) ⎨ б) ⎨ ⎪ 2x1 + 4x2 +11x3 +16x4 =146, ⎪2x1 + 3x2 + x3 + x4 =1, ⎩⎪ x1 + 9x2 + 9x3 +10x4 = 92. ⎪⎩ 5x1 + 5x2 + 2x3 = 2. ⎧ x1 + 2x2 + 3x3 + 4x4 = 20, ⎧ 2x1 − 4x2 + 3x3 − 2x4 = 3, ⎪ 2x + 5x + 9x +14x = 55, ⎪ 18. а) ⎨⎪ 1 2 3 4 б) ⎨⎪ x1 − 2x2 − x x3 − 4 = −2, ⎪ 3x1 + 9x2 +19x3 + 34x4 =111, ⎪ 3x1 − 6x2 + 5x3 − 3x4 = 5, ⎩⎪4x1 +14x2 + 34x3 + 68x4 =195. ⎩⎪4x1 − 8x2 − 3x3 − 4x4 = −3. ⎧ x x1 − 2 − 2x3 − 3x4 = −8, ⎧ 2x x1 + 2 + x4 = 2, ⎪⎪x1 − 2x2 − 4x3 − 6x4 = −11, ⎪⎪4x1 + 3x2 + x3 − 2x4 = −1, 19. а) ⎨ б) ⎨ ⎪11x x1 − 2 + x3 + 8x4 = −53, ⎪ 9x1 + 3x2 − x3 + 2x4 = 2, ⎪⎩ 2x1 + 2x2 + x3 − 5x4 = 5. ⎪⎩ x1 + 3x2 + 2x x3 − 4 = 3. |
⎪7x1 + 9x2 − 3x3 + 6x4 = 7, ⎩⎪5x1 + 9x2 − 3x3 + 6x4 = 5.
⎧ x x1 + 2 + x3 + x4 = 5, ⎪⎪ 2x − 3x + x x− = 0, ⎧ 2x x1 − 2 − x3 − 2x4 = −1,
⎪3x − 4x − 8x −13x = −9,
⎪
20. а) ⎨ 1 2 3 4 б) ⎨ 1 2 3 4
⎪3x1 + 4x2 − 2x3 + 6x4 = −1, ⎪ x x1 − 2 − 2x3 − 3x4 = −2,
⎪⎩ 5x1 + 4x3 + 2x4 =12. ⎪⎩ 3x1 − 2x2 − 4x3 − 5x4 = −3.
⎧ 7x1 +14x2 + 20x3 + 27x4 = 0, ⎧ 2x x1 + 2 − 4x x3 − 4 = 0,
⎪⎪5x1 +10x2 +16x3 + 21x4 = −2, ⎪⎪ x x1 + 2 − 3x3 = −1,
⎪ x1 + 2x2 + 3x3 + 4x4 = 0, ⎪x1 + 3x2 − 7x3 + 2x4 = −5, ⎪⎩ 3x1 + 5x2 + 6x3 +13x4 = 5. ⎪⎩ 3x x1 + 2 − x3 − 4x4 = 5.
⎧ 3x1 − 8x 2x x3 − 4 = 3, ⎧ x1 − 4x2 + 2x = −1,
⎪ 5x − 7x − 3x − 8x = 5, ⎪
22. ⎪⎨ 1 3 4 ⎪⎨2x1 − 3x2 − x3 − 5x4 = −7,
⎪3x1 −11x2 + 5x3 + 2x4 = 3, ⎪3x1 − 7x2 + x3 − 5x4 = −8, ⎪⎩ x x1 − 2 − x3 − 2x4 = −3. ⎩⎪ x2 − x3 − x4 = −1.
⎧ x1 − 2x2 + 4x4 = −3, ⎧2x1 + 3x2 − x3 + x4 = 2,
⎪⎪ 3x x− − 2x = 1, ⎪⎪ x + 2x + x x− =1,
23. а) ⎨ 1 2 3 б) ⎨ 1 2 3 4
⎪2x x1 + 2 − 2x3 − 4x4 = 4, ⎪ 3x1 + 5x2 = 3,
⎪⎩x1 + 3x2 − 2x3 − 8x4 = 6. ⎪⎩x x1 + 2 − 2x3 + 2x4 =1.
⎧ x1 + 3x2 − 2x3 + 3x4 =1, ⎧ 7x1 − 5x2 − 2x3 − 4x4 = 8,
⎪⎪ 2x1 + 4x2 − x3 + 3x4 = 2, ⎪⎪−3x1 + 2x2 + x3 + 2x4 = −3,
⎪3x1 + 5x2 − 2x3 + 3x4 =1, ⎪
⎩⎪2x1 + 8x2 − 3x3 + 9x4 = 2. ⎪⎩
2x x1 − 2 − x3 − 2x4 =1, −x2 + x3 + 2x4 = 3.
⎧ x x1 + 2 − 6x3 − 4x4 = 6, ⎧
⎪⎪ 3x x1 − 2 − 6x3 − 4x4 = 2, ⎪⎪ 2x1 + 7x2 + 3x3 + x4 = 5, x1 + 3x2 + 5x3 − 2x4 = 3,
⎪ 2x1 + 3x2 + 9x3 + 2x4 = 6, ⎪ x1 + 5x2 − 9x3 + 8x4 =1,
⎪⎩3x1 + 2x2 + 21x3 + 8x4 = −7. ⎩⎪5x1 +18x2 + 4x3 + 5x4 =12.
26 – 30. Найти значения параметра c, при которых система линейных уравнений: а) не имеет решений; б) имеет бесконечно много решений и найти эти решения.
⎧ x1 + 2x2 + 2x3 + 3x4 = 5, ⎧ 3x x1 + 2 − x x3 − 4 = 2,
⎪⎪ x1 + 2x2 + x3 + 2x4 =1, ⎪⎪ x x1 − 2 + x x3 − 4 = 0,
⎪x1 + 2x2 + 4x3 + 5x4 =13, ⎪ x1 + 3x2 − 3x3 + x4 = 2,
⎩⎪x1 + 2x2 + 3x cx3 + 4 =11. ⎪⎩x1 − 5x2 + 5x3 − 3x4 = c.
⎧2x1 + 3x2 + 7x3 − 2x4 = −1, ⎧ 4x1 + 5x2 + x3 + 3x4 =1,
⎪⎪ 2x1 + 3x2 − 2x3 + 7x4 = 2, ⎪⎪7x1 + 6x2 − 5x3 + 2x4 = 2,
⎪ 2x1 + 3x cx2 + 3 + x4 = 0, ⎪ x1 + 4x2 + 7x3 + 4x4 = 0,
⎪⎩ 2x1 + 3x2 + x3 + 4x4 = −3. ⎩⎪cx1 + 9x2 + 8x3 + 7x4 =1.
⎧ 5x1 − 3x 2x3 + 4x4 = 3, ⎧cx x1 + 2 + 2x3 + 3x4 =1,
⎪⎪ 4x1 − 2x + 3x3 + 7x4 =1, ⎪⎪x cx1 + 2 + 3x3 + 2x4 =1,
⎪ 8x1 − 6x2 − x3 − 5x4 = 9, ⎪ x x1 + 2 + x3 + 4x4 =1,
⎩⎪7x1 − 3x2 + 7x3 +17x4 = c. ⎩⎪ x1 + x2 + 4x3 + x4 = c.
⎧ 2x x1 − 2 + 3x3 + 4x4 = 5, ⎧ 3x1 − 8x2 + 2x x3 − 4 = 3,
⎪ 4x1 − 2x2 + 5x3 + 6x4 = 7, ⎪⎪ 5x1 − 7x2 − 3x3 − 8x4 = 5,
⎪
⎪ 6x1 − 3x2 + 7x3 + 8x4 = c, ⎪3x1 −11x2 + 5x3 + 2x4 = 3, ⎪⎩2x1 − 4x2 + 9x3 +10x4 =11. ⎪⎩ x1 + cx2 − x3 + 2cx4 = −c.
⎧x x1 + 2 + x cx3 + 4 =1, ⎧ x x1 + 2 + x3 + 4x4 =1,
⎪⎪x x cx x1 + 2 + 3 + 4 =1, ⎪⎪ x1 + x2 + 4x3 + x4 = c,
⎪x cx1 + 2 + x x3 + 4 =1, ⎪x cx1 + 2 + 3x3 + 2x4 =1,
⎩⎪cx x1 + 2 + x3 + x4 =1. ⎩⎪cx x1 + 2 + 2x3 + 3x4 =1.
Задание 6. 1 – 25. Даны три вершины параллелограмма ABCD .
Найти координаты четвертой вершины и угол между диагоналями:
|
1. A(1; 2),− B( 3− ;4), C(3;3); |
2. A( 4− ;3), B( 7− ;2), C( 1− ;−1); |
||
|
3. A(2;3), B(5;2), C( 1− −; 1); |
4. A( 1− ;2), B(3; 4),− C( 3− ;−3); |
||
|
5. A(4;4), B(7;3), C(1;0); |
6. A(3;5), B(6;4), C(0;1); |
||
|
7. A(4;5), B(7;4), C(1;1); |
8. A(5;3), B(8;2), C(2;−1); |
||
|
9. A(2;5), B(5;4), C( 1− ;1); |
10. A( 2− ;5), B( 5− ;4), C(1;1); |
||
|
11. A( 2− ;3), B( 5− ;2), C(1;−1); |
12. A( 4− ;5), B( 7− ;4), C( 1− ;1); |
||
|
13. A(4;7), B(10;3), C( 2− ;−1); |
14. A( 2− ; 3),− B( 5− ; 2),− C(1;1); |
||
|
15. A( 3− ; 5),− B( 6− ; 4),− C(0;1); |
16. A( 4− ;2), B(2;3), C(1;0); |
||
|
17. A( 4− ;2), B( 1− ;5), C(0;1); |
18. A( 5− ; 3),− B( 8− ; 2),− C( 2− ;1); |
||
|
19. A(4;3), B( 2− ;0), C( 1− ;−4); |
20. A( 1− ;1), B(5;4), C(2;5); |
||
|
21. A(7;5), B(2;3), C(3;−2); |
22. A(2; 1),− B( 5− ;2), C(0;4); |
||
|
23. A(3;3), B(5;1), C(0;−1); 25. A( 5− ;3), B(0;4), C(4;1); |
24. A(5;6), B(8;3), C(2;−1). |
||
26 –30. Диагонали параллелограмма ABCD пересекаются в точке O . Найти координаты его вершин и острый угол между сторонами, если:
|
26. O(1;1), AC(2;3), BD( 2− −; 2); |
27. O(2;0), AC(5; 1),− BD(2;3); |
|
28. O( 1− ;2), AC( 2− −; 3), BD(2;4); 30. O(3; 1),− AC(1;4), BD( 2− ;3). |
29. O( 1− ;3), AC(1;4), BD(3;−1). |
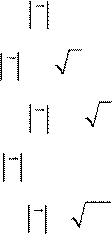
Задание 7. 1 – 10. Вектор x перпендикулярен оси Ox и вектору p и образует острый угол с осью Oy . Найти координаты вектора x , если:
1. p= (1;2;6), x = 2. p = ( 7− ;3; 4),− x =10;
3. p = −( 2;4;3), x = 5; 4. p= (6;1;7), x = 5 2 ;
5. p= (1;2;6), x = 2 2 ; 6. p= − −( 4; 3;6), x = 2 5 ;
7. p = −( 1;5;12), x = 26; 8. p = (2;5;0), x = 3;
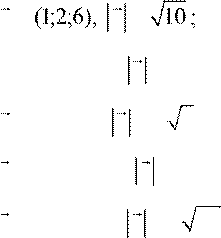
9. p=
−(2;
1;6), x = 2 37 ; 10.
p=
−(7;
2;5), x = 29 .
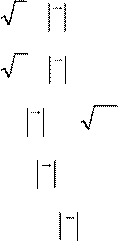
11 – 20. Вектор x перпендикулярен оси Oy и вектору p и образует тупой угол с осью Oz. Найти координаты вектора x , если:
11. p = (3; 6;4),− x = 30; 12. p= −(2; 1;2 3), x = 8;
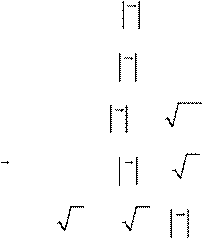
13. p
=
(9;7;12),
x = 20; 14.
p=
−(2;
3;3 5), x = 7;
15. p= (6;7;2), x = 2 10; 16. p= −( 1;11;3), x = 3 10 ;
17. p= (8;12;8), x = 3 2; 18. p = (0; 4; 9),− − x =1;
19. p= −( 2;1;− 2), x = 2; 20. p = (20; 3− ; 15),− x = 25.
21 – 30. Вектор x перпендикулярен оси Oz и вектору p и образует острый угол с осью Ox . Найти координаты вектора x , если:
21. p= (4;1; 7),− x = 17 ; 22. p = ( 30;16− ;5), x = 68;
23. p = (24;10;9), x = 39; 24. p = ( 18; 24− − ;0), x =15;
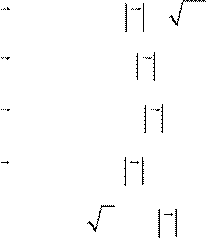
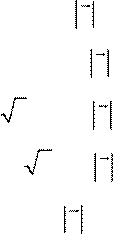
25. p=
(6
2;3;7), x = 27; 26.
p=
(4;4
3; 11),− x
=
24;
27. p = (9;0;14), x =8;
28. p= (
1−
−;
2 2;5), x =12;
29. p= −( 5;2 6;2), x =14; 30. p = (8; 15;3),− x = 51.
Задание 8. Найти угол между векторами p и q , если:
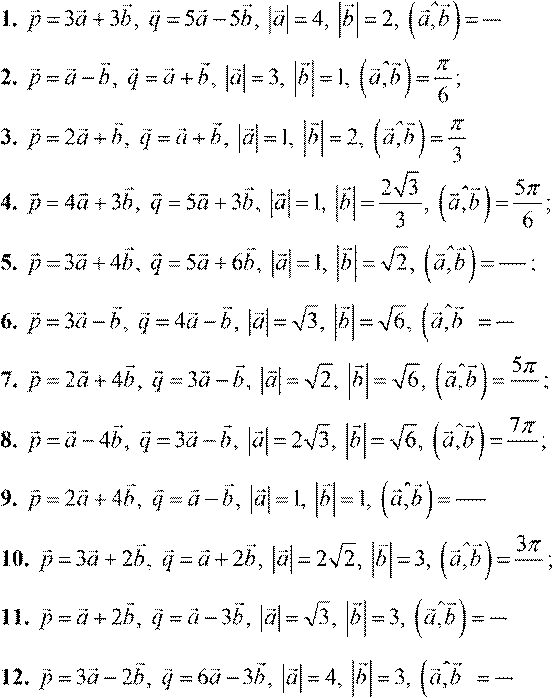π
;
2
;
6
3π
4 π
) ;
4
6
4
2π
;
3
4 π
= ;
6
π
) = ;
3
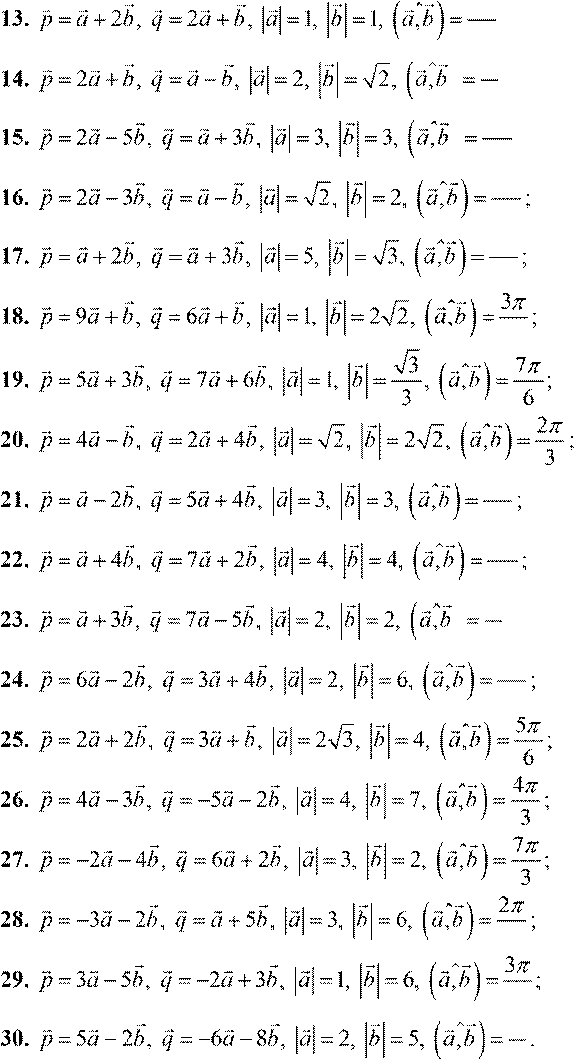5π
= ;
3
π b = ) ;
4
2π
) = ;
3
7π
4
5π
6
b = 2 2,
4
a =
4π
3
2π
3 π
) = ;
3
5π 3
3
2 π
2
Задание 9. Даны вершины треугольника ABC : A(x y1; 1), B x( 2; y2) и
C x( 3; y3). Найти: а) уравнение медианы AM ;
б) уравнение прямой, проходящей через вершину B параллельно медиане
AM ; в) уравнение высоты BH ;
г) угол между медианой AM и высотой BH ; д) площадь треугольника ABC .
|
1. A(1; 3),− B(8;0), C(4;8); |
2. A(5; 4),− B( 1− ;2), C(5;1); |
|
|
3. A(2;3), B(5;0), C(7;−5); |
4. A(1;1), B(2;5), C( 6− ;7); |
|
|
5. A( 1− ;3), B(2; 5),− C(0;4); |
6. A(10;5), B(3;2), C(6;−5); |
|
|
7. A( 3− ;5), B(7; 1),− C(2;9); |
8. A( 2− ;4), B(0;3), C(1;7); |
|
|
9. A( 1− ;7), B(7; 5),− C(3;−7); |
10. A( 2− ;1), B(2; 2),− C(8;6); |
|
|
11. A(3;6), B( 3− ;5), C(3;−6); |
12. A(2;5), B(3;8), C(10;5); |
|
|
13. A(1; 3),− B(3;4), C(7;−2); |
14. A( 6− ;3), B(8;10), C(2;−6); |
|
|
15. A(1;6), B(9; 2),− C( 5− ;−4); |
16. A(5;1), B(0;3), C(2;5); |
|
|
17. A( 3− ;4), B(9;0), C(1;−8); |
18. A( 5− ;0), B(2;8), C(7;−3); |
|
|
19. A(1;1), B(10;13), C(13;6); |
20. A(2;2), B( 1− ;6), C( 5− ;3); |
|
|
21. A( 2− ;3), B(5; 2),− C( 3− ;−1); |
22. A(1;4), B(3; 9),− C( 5− ;2); |
|
|
23. A(7;4), B(3; 6),− C( 5− ;2); |
24. A( 3− ;12), B(3; 4),− C(5;8); |
|
|
25. A(1;8), B(3;4), C(4;2); |
26. A(4;2), B(7; 2),− C(1;6); |
|
|
27. A(2; 2),− B(3; 5),− C(5;7); |
28. A(1; 1),− B(3;5), C( 7;11)− ; |
|
|
29. A(4;1), B(7;5), C( 4− ;7); |
30. A(10; 1)− , B(6; 9),− C( 4− ;1). |
Задание 10. Решить следующие задачи:
1. Даны две стороны параллелограмма 2x − y = 0, x −3y = 0 и точка пересечения его диагоналей M(2;3). Составить уравнения диагоналей.
2. Две стороны треугольника заданы уравнениями 5x − 2y −8 = 0 и 3x − 2y −8 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны.
3. Даны уравнения стороны ромба x +3y +12 = 0 и его диагонали 2x + y + 4 = 0. Составить уравнения остальных сторон ромба, зная, что точка M( 4− ;4) лежит на его стороне, параллельной данной.
4. Составить уравнения сторон треугольника ABC , зная одну из его вершин A(3;0) и уравнения двух медиан 7x −5y +15 = 0, 4x + y + 6 = 0.
5.
Составить
уравнение прямой, проходящей через начало координат, если известно, что длина
ее отрезка, заключенного между прямыми 3x + 4y
−
7
=
0
и 3x + 4y +8
=
0,
равна 3 2 .
6. Даны смежные вершины квадрата A(2;0) и B( 1− ;4). Составить уравнения его сторон.
7. Основанием равнобедренного треугольника служит прямая x + 2y = 0, а боковой стороной – прямая x − y + 6 = 0. Составить уравнение высоты, опущенной из точки пересечения данных сторон на третью сторону треугольника.
8. Составить уравнения сторон прямоугольника, если известны его вершина A( 1− ;3), точка L(0;2), лежащая на стороне AB, точка M(1;2), лежащая на стороне BC и точка N(2;1) пересечения его диагоналей.
9. Даны уравнения двух сторон треугольника 2x − y = 0, 5x − y = 0 и уравнение 3x − y = 0 одной из его медиан. Составить уравнение третьей стороны треугольника, зная, что она проходит через точку K(3;9) и найти координаты его вершин.
10. Даны вершины треугольника A( 6− ; 3),− B( 4− ;3), C(9;2). На внутренней биссектрисе угла A найти такую точку M , чтобы четырехугольник ABMC оказался трапецией.
11. Длина сторон ромба с острым углом 60 равна 2. Диагонали ромба пересекаются в точке M(1;2), причем меньшая диагональ параллельна оси ординат. Составить уравнения сторон и диагоналей ромба.
12. Составить уравнения сторон треугольника, зная его вершину C(4;−1), а также уравнения высоты 2x −3y +12 = 0 и медианы 2x +3y = 0, проведенных из одной вершины.
13. Точка A(1;2) является серединой одного из оснований прямоугольной трапеции, а точка B(3;−1) – середина средней линии.
Боковая сторона, перпендикулярная основаниям, лежит на прямой 4x −3y + 2 = 0. Составить уравнения остальных сторон.
14. Через точку A( 1− ;1) провести прямую так, чтобы середина ее отрезка
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
