Актуальность разработки электропривода компрессорной установки. Обзор основных типов компрессорных установок

требование удовлетворяют две механические характеристики при углах управления равных 40° и 0°.

По известным паспортным данным асинхронного двигателя и параметрам Г-образной схемы замещения рассчитываю параметры Т-образной схемы замещения и параметры блоков модели.

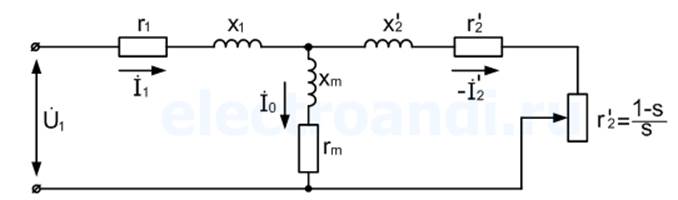
Рисунок 2.6 – Т-образная схема замещения

Номинальный фазный ток статора:

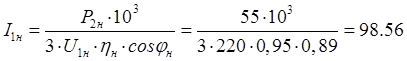A.           

Базисное значение сопротивления:

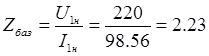Ом.                          

Угловая частота тока:

с^-1.                         

Реактивное сопротивление рассеяния статора в относительных единицах:

.   

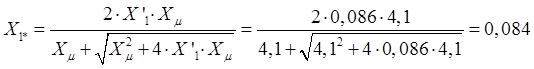Коэффициент, связывающий параметры машин в Т и Г-образных схемах замещения:

.                              

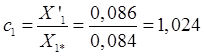Реактивное сопротивление рассеяния фазы статора:

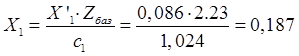Ом.                  

Активное сопротивление фазы статора:

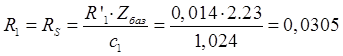Ом.                

Индуктивность рассеяния фазы статора:

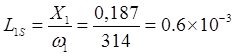Гн.                     

Реактивное сопротивление рассеяния приведенной обмотки ротора:

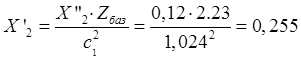Ом.                  

Активное сопротивление приведенной обмотки ротора:

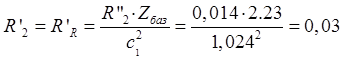Ом.          

Индуктивность рассеяния приведенной обмотки ротора:

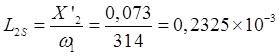Гн.                   

Реактивное сопротивление взаимоиндукции:

Ом.                 

Индуктивность взаимоиндукции:

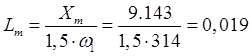Гн

Полная индуктивность фазы статора:

Гн.         

Полная индуктивность фазы ротора:

Гн.          

Суммарные потери мощности в двигателе:

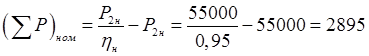Вт.             

Основные потери в обмотке статора:

 Вт.              

Намагничивающий ток:

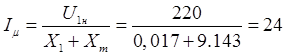 А.                 

Потери в стали статора:

 Вт

Основные потери в обмотке ротора:

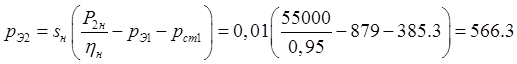Вт.  

Суммарные потери в стали и механике:

Вт.

Механические потери:

 Вт. 

Скорость идеального холостого хода двигателя:

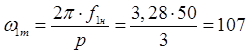 с^-1.                   

Номинальная скорость вращения двигателя:

 с^-1.             

Коэффициент трения:

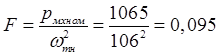Нм*с.                      

Скорость вращения электромагнитного поля статора можно определить по формуле:

.                                     

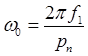При изменении частоты напряжения питания изменяется величина потока двигателя  и одновременно с изменением частоты напряжения необходимо регулировать его амплитуду.

.

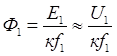При частотном регулировании величина относительного скольжения  зависит от разности скоростей вращающегося электромагнитного поля и ротора и от относительного значения  частоты питающего напряжения

,                                          

.                                          

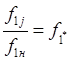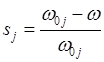Здесь , ,  - регулируемые значения частоты напряжения статора и соответствующие значения скорости вращения поля и скольжения;

 и  - номинальные значения частоты статора и скорости поля, соответствующие паспортным данным двигателя.

С учётом формулы 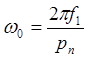 получим:

.                                 

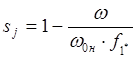Для анализа электромеханических характеристик двигателя при частотном регулировании возьмем Т-образная схема замещения двигателя.

; ;

; .

Однако, при номинальной частоте 50 Гц индуктивное сопротивление контура намагничивания  на порядок больше, чем активное сопротивление обмотки статора .

При анализе и расчёте электромеханических характеристик двигателя, работающего при постоянной номинальной частоте напряжения, сопротивлением  пренебрегаем.

Мощность процесса скольжения, выделяемая в цепи ротора электродвигателя, расходуется на нагрев обмоток ротора как следует из формулы:

 .   

Поэтому                                   ,                             откуда                                                .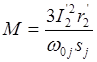                               

Учитывая, что отношения  и  гораздо меньше единицы и ими можно пренебречь, определим значение

.               

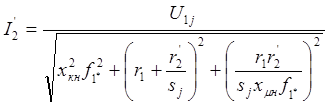Если подставить это выражение, то получим формулу для построения механических характеристик двигателя при переменных значениях величины и частоты напряжения питания.

.              

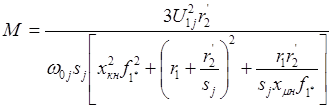Если предположить, что , найдём значение максимального момента и критического скольжения электродвигателя:

,                  

.                          

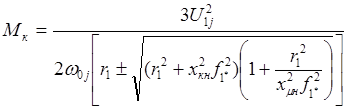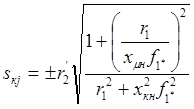Знак (+) соответствует двигательному режиму, знак (-) – режиму рекуперативного торможения.

Если пренебрегать величиной активного сопротивления статора, то, для того чтобы при частотном регулировании сохранять критический момент постоянным, нужно величину напряжения изменять пропорционально изменению частоты.

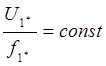, где                                                  .                                      

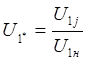При малых частотах, когда значение падения напряжения на сопротивлении  становится больше, поток двигателя уменьшается и соответственно уменьшается момент .

Следовательно, для того чтобы регулировать скорость асинхронного двигателя, сохраняя максимальный момент двигателя неизменным, необходимо величину напряжения уменьшать в меньшей степени, чем уменьшается частота, примерно в следующем соотношении:

.                        

Произведём расчет для частоты f₁=25 гц().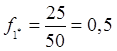

Так как 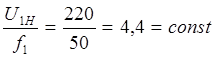, то  В, тогда В.

Согласно формуле критический момент определится как:

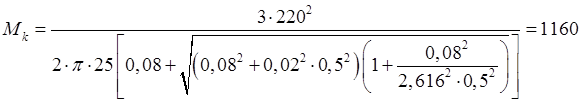Нм, а критическое скольжение ротора:

.

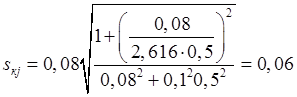Для остальных точек значение момента и скольжения определяются по формулам  и  соответственно.

Механические характеристики электродвигателя приведены на рисунке 2.7. Как видно закон управления U/f=const обеспечивает высокий запас устойчивости по скорости, жесткость механической характеристики и широкий диапазон регулирования скорости.

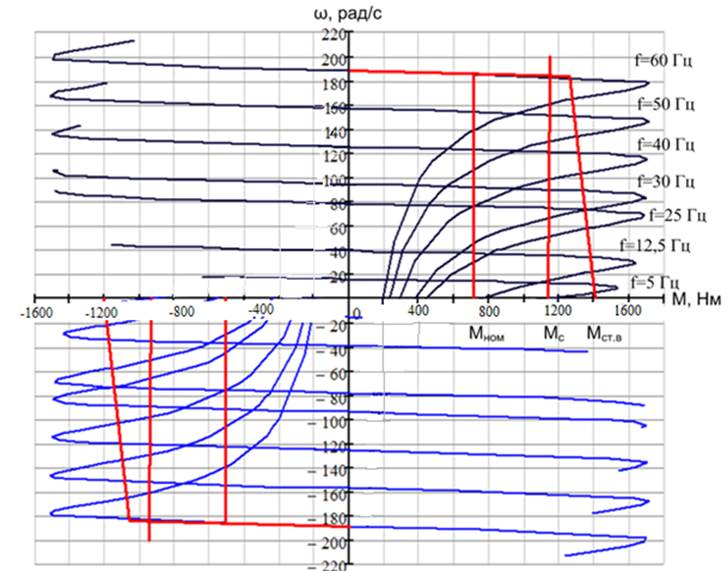
Рисунок 2.7 - Механические характеристики при разных частотах

2.5 Расчет переходных характеристик двигателя

В настоящее время в электроприводе при создании системы автоматического управления нашел широкое применение принцип подчиненного регулирования координат с последовательной коррекцией.

При построении таких систем объект управления представляется в виде цепочки последовательно соединенных звеньев с передаточными функциями W01(p), W02(p), W0i-1(p), W0i(p), выходными параметрами которых являются контролируемые координаты объекта: напряжение, частота, ток, скорость и т.д.

Для построения системы автоматизированного управления электроприводом  определяем передаточные функций объекта регулирования, обратных связей, синтезируем регуляторы координат и технологических параметров.

Рассмотрим при синтезе системы регулирования частоты вращения привода скипового подъемника упрощенную математическую модель асинхронного двигателя, с двумя регулируемыми координатами – момент и скорость двигателя.

Асинхронный двигатель по данной модели можно представить двумя звеньями с передаточными функциями

Механическая часть:

.                                           

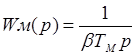Электромеханическая часть:

.                                 

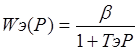Структурная схема модели двигателя представлена на рисунке 2.8.

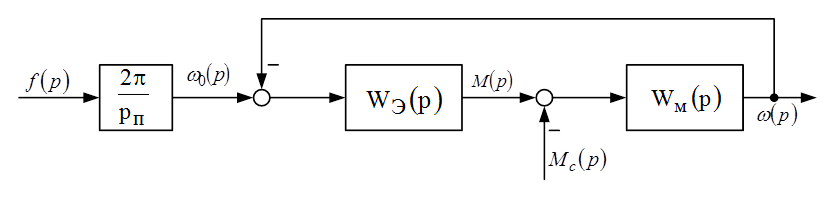
Рисунок 2.8 – Упрощенная структурная схема асинхронного двигателя

Основные параметры указанных звеньев β, Тм, Тэ, определяем по следующим формулам.

Коэффициент жесткости на рабочей характеристике:

           

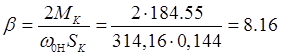
Электромеханическая постоянная времени:

                                                             

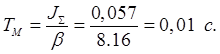
Эквивалентная электромагнитная постоянная времени цепей статора и ротора АД:

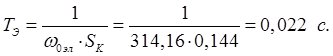                                 где:  – угловая скорость электромагнитного поля двигателя.

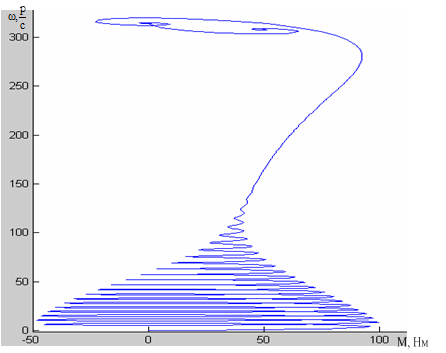
Рисунок 2.9 - Динамическая механическая характеристика АД полученная